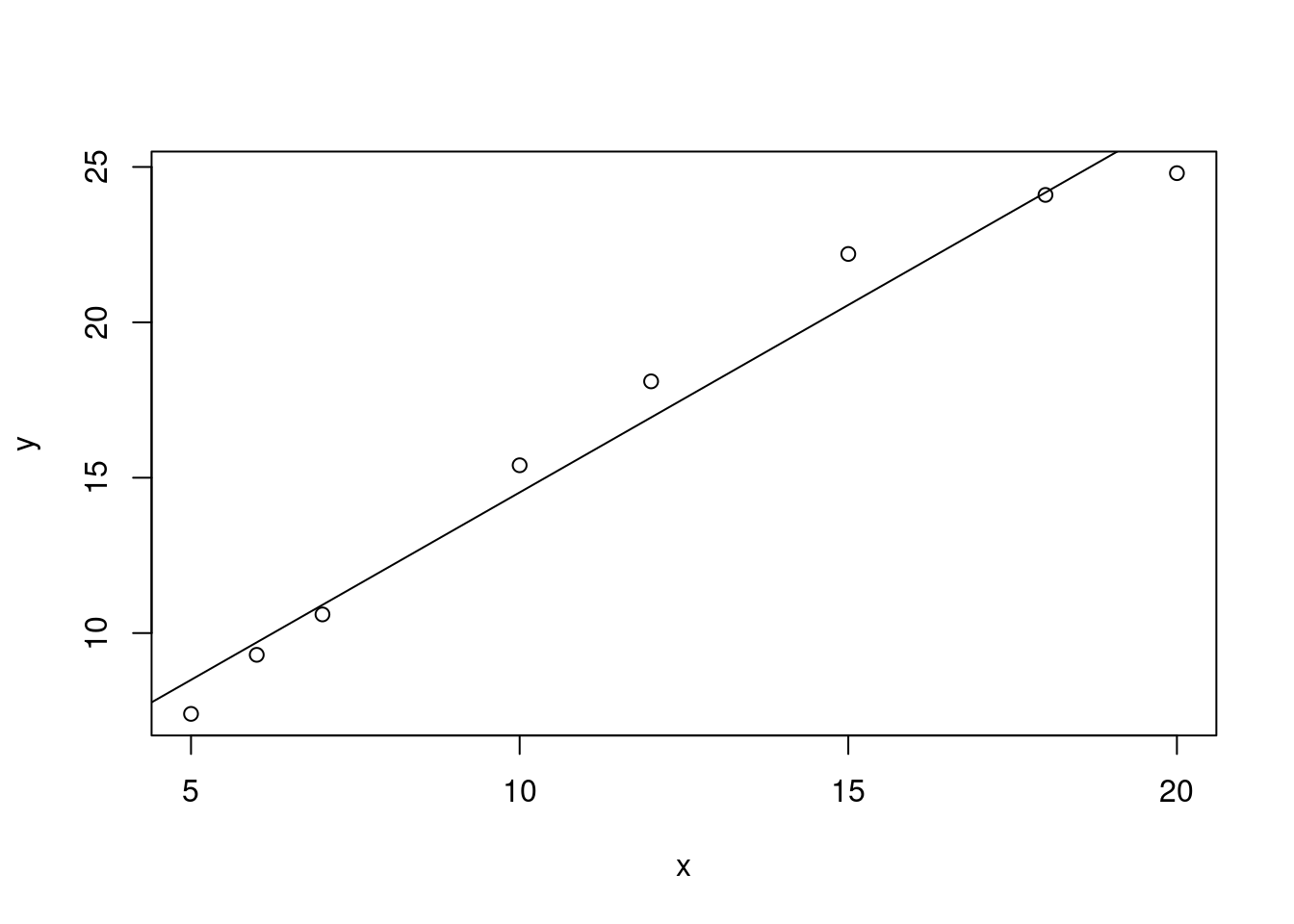工程和科学中的许多问题都涉及到：确定一组变量之间的关系。例如，在化学反应中，我们可能对化学反应的产物、反应时的温度以及所用催化剂的用量之间的关系感兴趣。了解这种不同变量之间的关系可以使我们预测不同温度和催化剂用量下的反应产物。
在许多情况下，存在一个单一的 响应变量（response variable）——也称之为 因变量（dependent variable）—— \(Y\)。因变量 \(Y\) 依赖于一组 输入变量（input variables）——也称之为 自变量（independent variables）——\(x_1, \ldots, x_r\) 的值。最简单的 因变量 \(Y\) 和 自变量 \(x_1, \ldots, x_r\) 之间的关系类型是线性关系。即，对于一组常数 \(\beta_0, \beta_1, \ldots, \beta_r\)，先行关系的等式为：
\[ Y = \beta_0 + \beta_1 x_1 + \cdots + \beta_r x_r \tag{9.1}\]
如果 \(Y\) 和 \(x_i\) 之间的关系如 式 9.1 所示，那么一旦学习到 \(\beta_i\)，我们就可以准确预测任意一组输入值的 \(Y\)。然而，实际上，几乎无法实现 100% 的精确预测，我们最多可以期望 式 9.1 在随机误差下（subject to random error）是有效的。此时，式 9.1 将表示为：
\[ Y = \beta_0 + \beta_1 x_1 + \cdots + \beta_r x_r + e \tag{9.2}\]
其中 \(e\) 表示随机误差，并假设随机误差是均值为 0 的随机变量。实际上，式 9.2 的另一种表达为：
\[ E[Y|\mathbf{x}] = \beta_0 + \beta_1 x_1 + \cdots + \beta_r x_r \tag{9.3}\]
其中 \(\mathbf{x} = (x_1, \ldots, x_r)\) 是 自变量，\(E[Y|\mathbf{x}]\) 是在给定输入 \(\mathbf{x}\) 下的结果的期望。
我们称 式 9.2 为 线性回归方程（linear regression equation）。式 9.2 描述了 因变量 \(Y\) 对一组 自变量 \(x_1, \ldots, x_r\) 的回归。我们称 \(\beta_0, \beta_1, \ldots, \beta_r\) 为 回归系数（regression coefficients），并且通常需要通过估计得到 回归系数。如果回归方程中只包含一个 自变量——即 \(r=1\)，我们称之为 简单回归方程（simple regression equation）；相比之下，如果回归方程包含多个 自变量，我们称之为 多元回归方程（multiple regression equation）。
因此，简单线性回归模型假设 \(Y\) 的均值与单个 自变量 的值之间存在线性关系，即：
\[ Y = \alpha + \beta x + e \tag{9.4}\]
其中，\(x\) 是自变量的值，也称为 输入水平（input level），\(Y\) 是对应的输出，\(e\) 代表均值为 0 的随机误差。
在回归分析中，而对于因变量和自变量的取值会有多种描述，例如对于：
我们在后续的章节中，会根据具体的场景来穿插使用这些术语。
例 9.1 考虑以下 10 对数据 \((x_i, y_i), i = 1, \ldots, 10\)，其中 \(y\) 是实验的百分比产量，\(x\) 是实验温度。
\[ \begin{array}{ccc|ccc} i & x_i & y_i & i & x_i & y_i \\ 1 & 100 & 45 & 6 & 150 & 68 \\ 2 & 110 & 52 & 7 & 160 & 75 \\ 3 & 120 & 54 & 8 & 170 & 76 \\ 4 & 130 & 63 & 9 & 180 & 92 \\ 5 & 140 & 62 & 10 & 190 & 88 \\ \end{array} \]
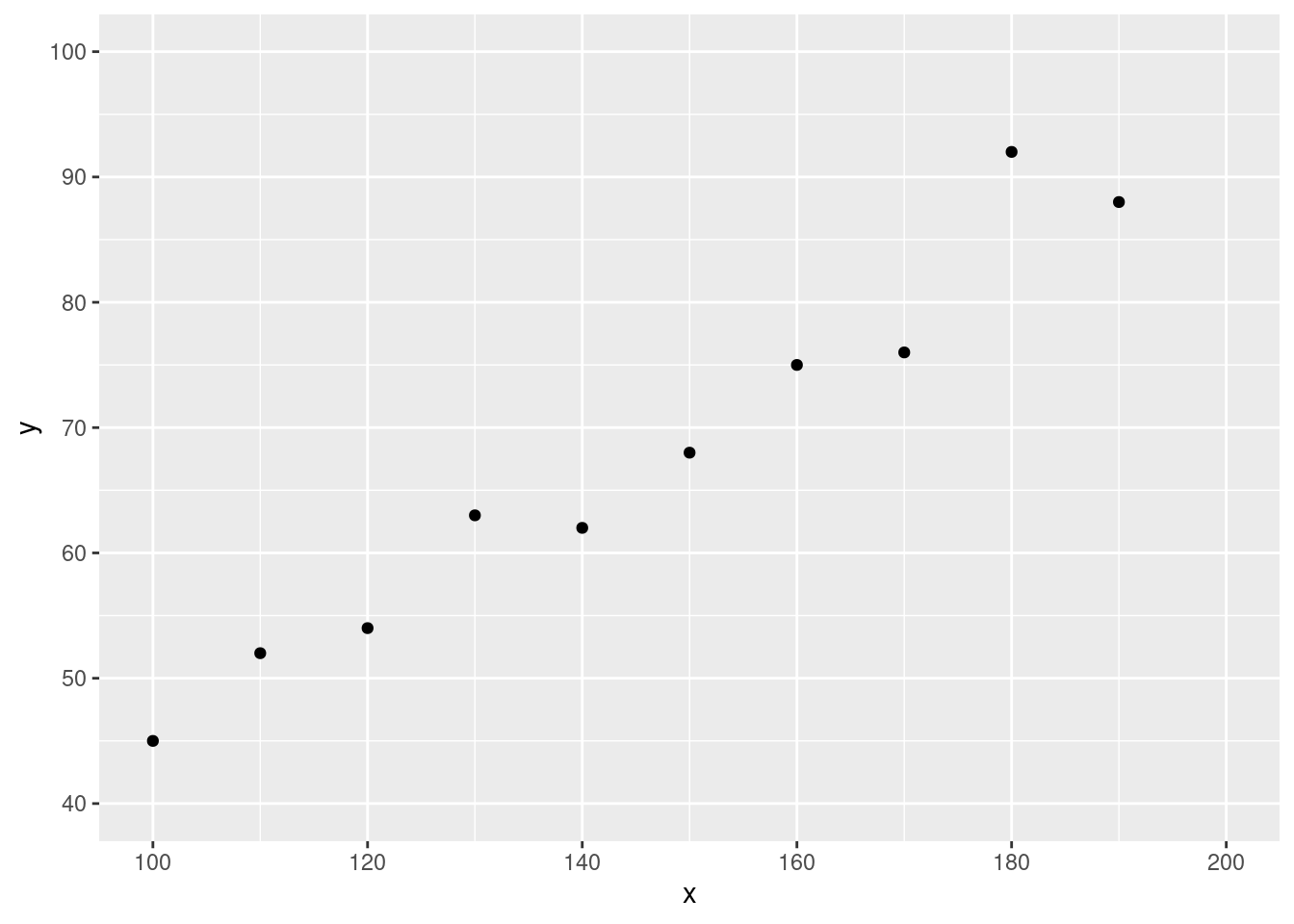
如上数据的散点图（scatter diagram）如 图 9.1 所示。
library(ggplot2)
x <- seq(100, 190, 10)
y <- c(45, 52, 54, 63, 62, 68, 75, 76, 92, 88)
df <- data.frame(x = x, y = y)
ggplot(df, aes(x = x, y = y)) +
geom_point() +
scale_x_continuous(breaks = seq(100, 200, 20), limits = c(100, 200)) +
scale_y_continuous(breaks = seq(40, 100, 10), limits = c(40, 100))
正如 图 9.1 的散点图所显示的那样，受随机误差的影响，\(y\) 和 \(x\) 之间似乎存在线性关系。因此，看起来，对于本例的数据而言，简单线性回归模型似乎是合适的。\(\blacksquare\)
假设对于输入值 \(x_i\)（\(i = 1, \ldots, n\)）的输出为 \(Y_i\)，我们将这些数据作为观察值并用于估计简单线性回归模型（式 9.4）中的 \(\alpha\) 和 \(\beta\)。
为了确定 \(\alpha\) 和 \(\beta\) 的估计，我们作如下推理：如果 \(A\) 是 \(\alpha\) 的估计，\(B\) 是 \(\beta\) 的估计，那么输入变量 \(x_i\) 的输出估计将是 \(A + Bx_i\)。由于实际输出是 \(Y_i\) ，因此实际输出和输出估计之间的平方差为 \((Y_i - A - Bx_i)^2\)，因此如果 \(A\) 和 \(B\) 是 \(\alpha\) 和 \(\beta\) 的估计，那么输出估计值和实际输出值之间的平方差的和（SS: the sum of the squared）为：
\[ SS = \sum_{i=1}^n (Y_i - A - Bx_i)^2 \tag{9.5}\]
最小二乘法（the least squares）选择让 SS 达到最小值的 \(A\) 和 \(B\) 以作为 \(\alpha\) 和 \(\beta\) 的估计。为了确定 \(A\) 和 \(B\)，我们首先对 SS 进行微分运算：
\(\frac{\partial SS}{\partial A} = -2 \sum_{i=1}^n (Y_i - A - Bx_i)\)
\(\frac{\partial SS}{\partial B} = -2 \sum_{i=1}^n x_i (Y_i - A - Bx_i)\)
令偏导数为零，得到令 \(A\) 和 \(B\) 最小化的方程：
\[ \begin{align} \sum_{i=1}^n Y_i &= nA + B \sum_{i=1}^n x_i \\ \sum_{i=1}^n x_i Y_i &= A \sum_{i=1}^n x_i + B \sum_{i=1}^n x_i^2 \end{align} \tag{9.6}\]
我们称 式 9.6 为 正规方程（the normal equations）。如果令：
\(\overline{Y} = \sum_i Y_i / n, \quad \overline{x} = \sum_i x_i / n\)
那么我们可以将第一个 正规方程 写为：
\[ A = \overline{Y} - B \overline{x} \tag{9.7}\]
把 \(A\) 的代入到第二个 正规方程 得到：
\(\sum_{i}{x_iY_i} = (\overline{Y}-B\overline{x})n\overline{x} + B \sum_{i}{x_i^2}\)
即，\(B\bigg(\sum_i{x_i^2} - n \overline{x}^2\bigg)=\sum_i{x_iY_i} - n\overline{x}\overline{Y}\)
即，\(B = \frac{\sum_i{x_iY_i} - n\overline{x}\overline{Y}}{\sum_i{x_i^2} - n \overline{x}^2}\)
因此，根据 式 9.7 和 \(n\overline{Y}=\sum_{i=1}^{n}{Y_i}\)，我们可以证明 命题 9.1。
命题 9.1 在数据集 \((x_i, y_i), i = 1, \ldots, n\) 上的 \(\beta\) 和 \(\alpha\) 的最小二乘法估计量分别为：
\(B = \frac{\sum_{i=1}^n x_i Y_i - \overline{x} \sum_{i=1}^n Y_i}{\sum_{i=1}^n x_i^2 - n\overline{x}^2}\)
\(A = \overline{Y} - B\overline{x}\)
我们称直线 \(A + Bx\) 为估计线性方程（the estimated regression line）。
我们可以使用 R 来获得数据对 \((x_1, y_1), ..., (x_n, y_n)\) 的估计线性方程。
x <- c(x_1, ..., x_n)
y <- c(y_1, ..., y_n)
df <- data.frame(x = x, y = y)
1fit <- lm(y ~ x, df)
2fitlm(y~x)，该模型为线性模型并且假定 \(y\) 是 \(x\) 的线性函数加上一个随机误差，并且我们将该模型命名为 fit。
fit 的估计线性方程。
例如：
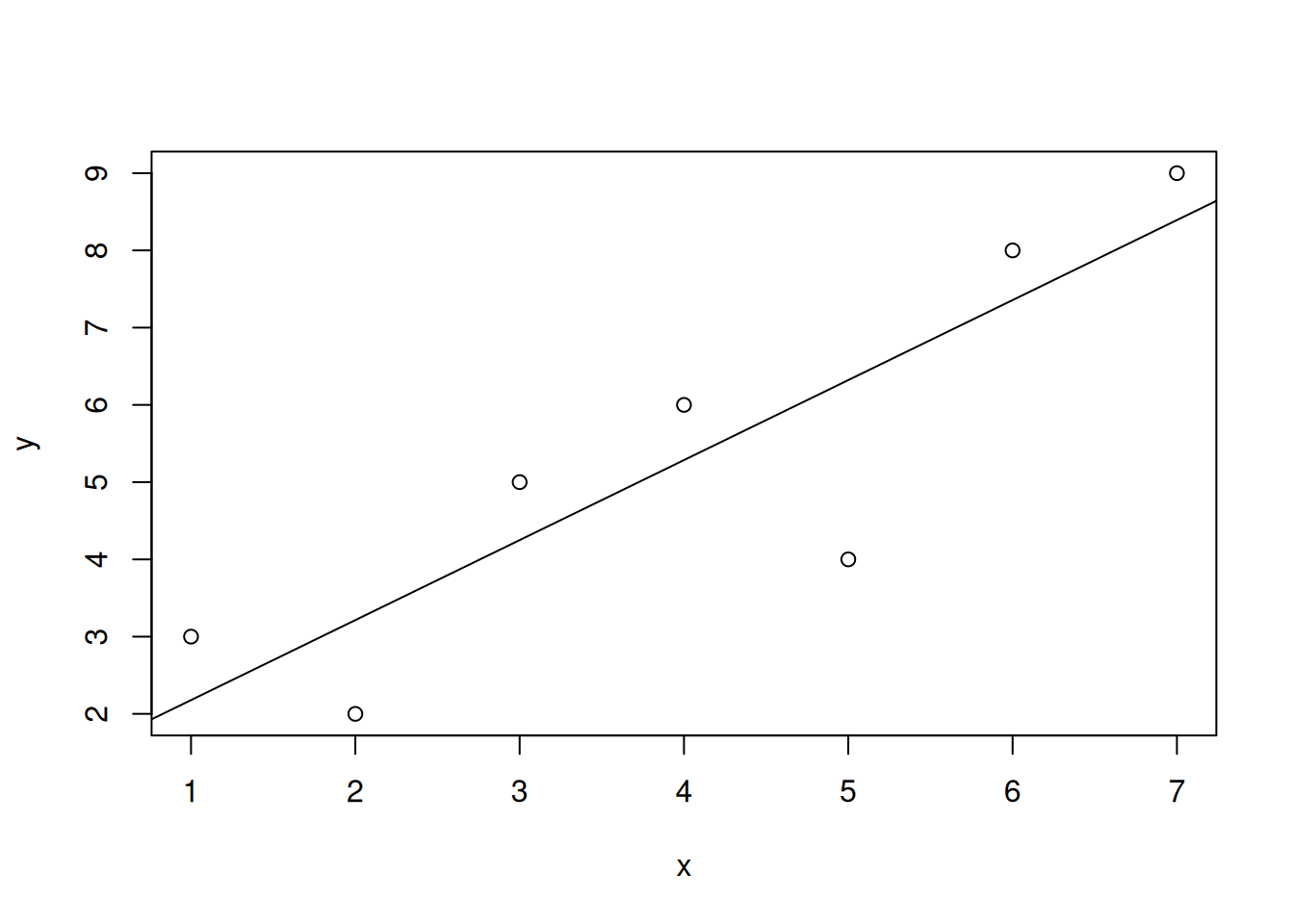
x <- c(1, 2, 3, 4, 5, 6, 7)
y <- c(3, 2, 5, 6, 4, 8, 9)
df <- data.frame(x = x, y = y)
fit <- lm(y ~ x, df)
fit
Call:
lm(formula = y ~ x, data = df)
Coefficients:
(Intercept) x
1.143 1.036 所以，根据如上的结果，估计线性方程为：\(y = 1.143 + 1.036x\)。
要获得估计线性方程图，首先输入 plot(x, y)，这将生成散点图。然后输入 abline(fit)，这将在散点图上添加估计线性方程的直线。
x <- c(1, 2, 3, 4, 5, 6, 7)
y <- c(3, 2, 5, 6, 4, 8, 9)
df <- data.frame(x = x, y = y)
fit <- lm(y ~ x, df)
plot(x, y)
abline(fit)
例 9.2 生产某种合成纤维所用的原材料储存在一个没有湿度控制的地方。该储存地点 15 天内的相对湿度和原材料样品的水分含量数据如下所示：
| 相对湿度（%） | 46 | 53 | 29 | 61 | 36 | 39 | 47 | 49 | 52 | 38 | 55 | 32 | 57 | 54 | 44 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 原材料含水量（%） | 12 | 15 | 7 | 17 | 10 | 11 | 11 | 12 | 14 | 9 | 16 | 8 | 18 | 14 | 12 |
将该线性回归模型命名为 moisture，并且利用 R 得到：
x <- c(46, 53, 29, 61, 36, 39, 47, 49, 52, 38, 55, 32, 57, 54, 44)
y <- c(12, 15, 7, 17, 10, 11, 11, 12, 14, 9, 16, 8, 18, 14, 12)
df <- data.frame(x = x, y = y)
moisture <- lm(y ~ x, df)
moisture
Call:
lm(formula = y ~ x, data = df)
Coefficients:
(Intercept) x
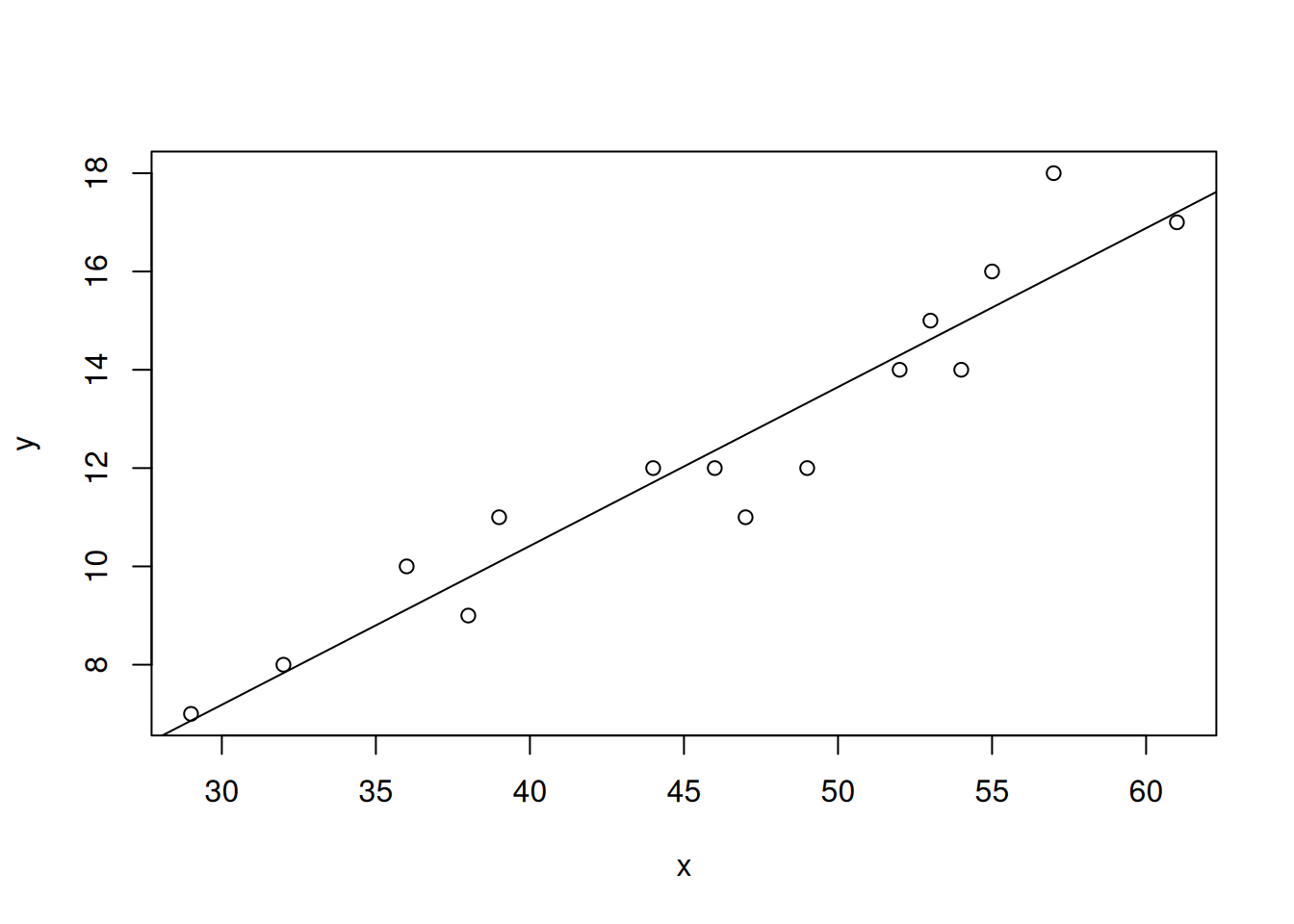
-2.5105 0.3232 数据的散点图和估计线性方程图为：
x <- c(46, 53, 29, 61, 36, 39, 47, 49, 52, 38, 55, 32, 57, 54, 44)
y <- c(12, 15, 7, 17, 10, 11, 11, 12, 14, 9, 16, 8, 18, 14, 12)
df <- data.frame(x = x, y = y)
moisture <- lm(y ~ x, df)
plot(x, y)
abline(moisture)
为了确定估计量 \(A\) 和 \(B\) 的分布，不能仅仅假设随机误差的均值为 0，我们有必要对随机误差做出额外的假设。通常，我们假设随机误差是均值为 0，方差为 \(\sigma^2\) 的独立的、正态分布随机变量。也就是说，如果输入值 \(x_i\) 对应的输出为 \(Y_i\)，那么 \(Y_1, \ldots, Y_n\) 相互独立，并且：
\(Y_i \sim \mathcal{N}(\alpha + \beta x_i, \sigma^2)\)
注意，上述假设认为随机误差的方差不依赖于输入值，而是一个常数。并且，我们假设 \(\sigma^2\) 的值是未知的，我们必须通过数据对 \(\sigma^2\) 进行估计。
根据 命题 9.1，\(\beta\) 的最小二乘估计量 \(B\) 可以表示为：
\[ B = \frac{\sum_{i}(x_i - \overline{x}) Y_i}{\sum_{i} x_i^2 - n\overline{x}^2} \tag{9.8}\]
因此，\(B\) 是独立、正态分布随机变量 \(Y_i, i = 1, \ldots, n\) 的线性组合，所以 \(B\) 本身也服从正态分布。根据 式 9.8，\(B\) 的均值和方差为：
\[ \begin{align} E[B] &= \frac{\sum_{i}(x_i - \overline{x}) E[Y_i]}{\sum_{i} x_i^2 - n\overline{x}^2} \\ &= \frac{\sum_{i}(x_i - \overline{x})(\alpha + \beta x_i)}{\sum_{i} x_i^2 - n\overline{x}^2} \\ &= \frac{\alpha \sum_{i}(x_i - \overline{x}) + \beta \sum_{i}x_i(x_i - \overline{x})}{\sum_{i} x_i^2 - n\overline{x}^2} \\ &= \beta \frac{\sum_i x_i^2 - \overline{x}\sum_i x_i}{\sum_i x_i^2 - n\overline{x}^2} \quad \because \sum_i(x_i - \overline{x}) = 0 \\ &= \beta \end{align} \]
因此，\(E[B] = \beta\)，所以 \(B\) 是 \(\beta\) 的无偏估计量。现在，我们计算 \(B\) 的方差。
\[ \begin{align} \textup{Var}(B) &= \frac{\textup{Var}\bigg( \sum_{i=1}^n (x_i - \overline{x}) Y_i \bigg)}{\bigg( \sum_{i=1}^n x_i^2 - n\overline{x}^2 \bigg)^2} \\ &= \frac{\sum_{i=1}^n (x_i - \overline{x})^2 \textup{Var}(Y_i)}{\bigg( \sum_{i=1}^n x_i^2 - n \overline{x}^2 \bigg)^2} \text{ by independence} \\ &= \frac{\sigma^2 \sum_{i=1}^n (x_i - \overline{x})^2}{\bigg( \sum_{i=1}^n x_i^2 - n \overline{x}^2 \bigg)^2} \\ &= \frac{\sigma^2}{\sum_{i=1}^n x_i^2 - n \overline{x}^2} \quad \because \sum_{i=1}^n (x_i - \overline{x})^2 = \sum_{i=1}^n x_i^2 - n \overline{x}^2 \end{align} \tag{9.9}\]
根据 式 9.8 以及 \(A = \frac{\sum_{i=1}^n Y_i}{n} - B \overline{x}\) 表明 \(A\) 也可以表示为独立正态分布随机变量 \(Y_i, i = 1, \ldots, n\) 的线性组合，因此 \(A\) 也服从正态分布。\(A\) 的均值为：
\[ \begin{align} E[A] &= \sum_{i=1}^n \frac{E[Y_i]}{n} - \overline{x} E[B] \\ &= \sum_{i=1}^n \frac{\alpha + \beta x_i}{n} - \overline{x} \beta \\ &= \alpha + \beta \overline{x} - \overline{x} \beta \\ &= \alpha \end{align} \]
因此，\(A\) 也是 \(\alpha\) 的无偏估计量。首先将 \(A\) 表示为 \(Y_i\) 的线性组合来计算 \(A\) 的方差，其结果为（详细的推导步骤作为练习留给读者）：
\[ \text{Var}(A) = \frac{\sigma^2 \sum_{i=1}^n x_i^2}{n \bigg( \sum_{i=1}^n x_i^2 - n \overline{x}^2 \bigg)} \tag{9.10}\]
\(Y_i - A - Bx_i, i = 1, \ldots, n\)，表示实际值（即 \(Y_i\)）与其最小二乘估计量（即 \(A + Bx_i\)）之间的差异，我们称之为 残差（residuals）。可以用残差的平方和：
\(SS_R = \sum_{i=1}^n (Y_i - A - Bx_i)^2\)
来估计随机误差的方差 \(\sigma^2\)。实际上，可以证明
\(\frac{SS_R}{\sigma^2} \sim \chi^2_{n-2}\)
也就是说，\(\frac{SS_R}{\sigma^2}\) 服从自由度为 \(n-2\) 的卡方分布，这意味着
\(E \left[ \frac{SS_R}{\sigma^2} \right] = n-2\)
或者
\(E \left[ \frac{SS_R}{n-2} \right] = \sigma^2\)
因此，\(\frac{SS_R}{n-2}\) 是 \(\sigma^2\) 的无偏估计量。此外，还可以证明 \(SS_R\) 与 \(A\) 和 \(B\) 是独立的。
关于为什么 \(\frac{SS_R}{\sigma^2}\) 服从自由度为 \(n-2\) 的卡方分布并且与 \(A\) 和 \(B\) 独立的合理性论证如下。
因为 \(Y_i\) 是独立正态随机变量，因此 \(\frac{(Y_i - E[Y_i])}{\sqrt{\text{Var}(Y_i)}}\)（\(i = 1, \ldots, n\)）服从标准正态分布，所以：
\(\sum_{i=1}^n \frac{(Y_i - E[Y_i])^2}{\text{Var}(Y_i)} = \sum_{i=1}^n \frac{(Y_i - \alpha - \beta x_i)^2}{\sigma^2} \sim \chi^2_n\)
现在，如果我们用估计量 \(A\) 和 \(B\) 替代 \(\alpha\) 和 \(\beta\)，那么将失去 2 个自由度，因此 \(\frac{SS_R}{\sigma^2}\) 服从自由度为 \(n-2\) 的卡方分布并不令人惊讶。
事实上，\(SS_R\) 与 \(A\) 和 \(B\) 的独立性与一个基本结果非常相似，即在正态分布抽样中，\(\overline{X}\) 和 \(S^2\) 是独立的（定理 6.2）。实际上，\(\overline{X}\) 和 \(S^2\) 的独立性表明，如果 \(Y_1, \ldots, Y_n\) 是均值为 \(\mu\)、方差为 \(\sigma^2\) 的正态分布样本，那么平方和 \(\sum_{i=1}^n (Y_i - \mu)^2 / \sigma^2\) 服从自由度为 \(n\) 的卡方分布。如果用均值的估计量 \(\overline{Y}\) 替代 \(\mu\) 得到新的平方和 \(\sum_{i} (Y_i - \overline{Y})^2 / \sigma^2\)，那么这个量（等于 \((n-1)S^2 / \sigma^2\)）将与 \(\overline{Y}\) 独立，并且将服从自由度为 \(n-1\) 的卡方分布。由于 \(SS_R / \sigma^2\) 是通过在平方和 \(\sum_{i=1}^n (Y_i - \alpha - \beta x_i)^2 / \sigma^2\) 中用估计量 \(A\) 和 \(B\) 来分别替代 \(\alpha\) 和 \(\beta\)，因此这个量可能与 \(A\) 和 \(B\) 是独立的。
当 \(Y_i\) 是正态分布随机变量时，最小二乘估计量也是最大似然估计量。为了验证这一点，注意到 \(Y_1, \ldots, Y_n\) 的联合密度由下式给出：
\[ \begin{align} f_{Y_1, \ldots, Y_n}(y_1, \ldots, y_n) &= \prod_{i=1}^n f_{Y_i}(y_i) \\ &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi} \sigma} e^{-(y_i - \alpha - \beta x_i)^2 / 2\sigma^2} \\ &= \frac{1}{(2\pi)^{n/2} \sigma^n} e^{-\sum_{i=1}^n (y_i - \alpha - \beta x_i)^2 / 2\sigma^2} \\ \end{align} \]
因此，\(\alpha\) 和 \(\beta\) 的最大似然估计量恰好是使 \(\sum_{i=1}^n (y_i - \alpha - \beta x_i)^2\) 最小的值，即最小二乘估计量。
如果我们令：
\(S_{xY} = \sum_{i=1}^n (x_i - \overline{x})(Y_i - \overline{Y}) = \sum_{i=1}^n x_i Y_i - n \overline{x} \overline{Y}\)
\(S_{xx} = \sum_{i=1}^n (x_i - \overline{x})^2 = \sum_{i=1}^n x_i^2 - n \overline{x}^2\)
\(S_{YY} = \sum_{i=1}^n (Y_i - \overline{Y})^2 = \sum_{i=1}^n Y_i^2 - n \overline{Y}^2\)
则最小二乘估计量可以表示为：
\(B = \frac{S_{xY}}{S_{xx}}\)
\(A = \overline{Y} - B\overline{x}\)
因此，我们得到如下的残差的平方和的计算等式：
\[ SS_R = \frac{S_{xx}S_{YY} - S_{xY}^2}{S_{xx}} \tag{9.11}\]
命题 9.2 对本节的内容进行了总结。
命题 9.2 假设因变量 \(Y_i, i = 1, \ldots, n\) 是均值为 \(\alpha + \beta x_i\)、方差为 \(\sigma^2\) 的独立的、正态分布随机变量。\(\beta\) 和 \(\alpha\) 的最小二乘估计量为：
\(B = \frac{S_{xY}}{S_{xx}}, \quad A = \overline{Y} - B\overline{x}\)
其分布为：
\(A \sim \mathcal{N} \left( \alpha, \frac{\sigma^2 \sum_{i} x_i^2}{n S_{xx}} \right)\)
\(B \sim \mathcal{N} \left( \beta, \frac{\sigma^2}{S_{xx}} \right)\)
此外，如果我们令：
\(SS_R = \sum_{i} (Y_i - A - Bx_i)^2\)
表示残差平方和，那么：
\(\frac{SS_R}{\sigma^2} \sim \chi^2_{n-2}\)
并且 \(SS_R\) 与最小二乘估计量 \(A\) 和 \(B\) 是独立的。同时，\(SS_R\) 可以通过如下的方式来计算：
\(SS_R = \frac{S_{xx}S_{YY} - (S_{xY})^2}{S_{xx}}\)
可以使用 R 计算 \(S_{xY}\)，\(S_{xx}\)，\(S_{YY}\)，\(SS_R\)：
x <- c(x_1, ..., x_n)
y <- c(y_1, ..., y_n)
Sxy <- sum(x * y) - n * mean(x) * mean(y)
Sxx <- sum(x * x) - n * mean(x)^2
Syy <- sum(y * y) - n * mean(y)^2
SSR <- (Sxx * Syy - Sxy^2) / Sxx习题 9.1 下面的数据中，\(x\) 为某种产品的湿混合物的水分，\(Y\) 为最终产品的密度。
| \(x_i\) | \(y_i\) |
|---|---|
| 5 | 7.4 |
| 6 | 9.3 |
| 7 | 10.6 |
| 10 | 15.4 |
| 12 | 18.1 |
| 15 | 22.2 |
| 18 | 24.1 |
| 20 | 24.8 |
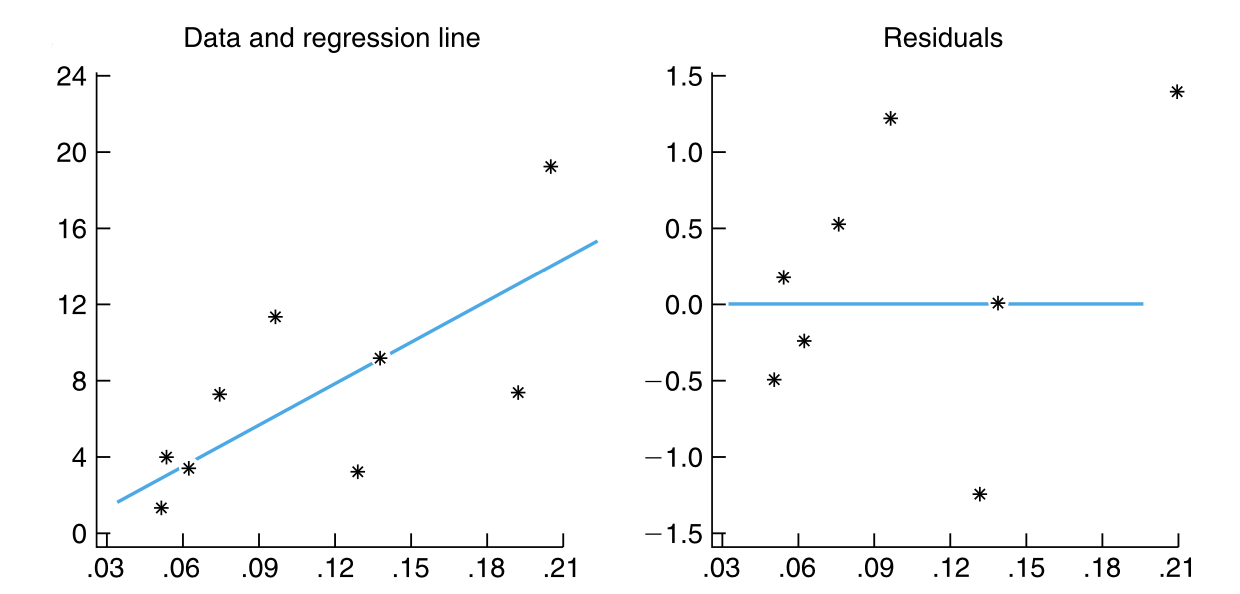
为这些数据拟合一条线性曲线，并确定回归方程的残差的平方和 \(SS_R\)。
解 9.1. 使用 R 计算 \(SS_R\)：
x <- c(5,6,7,10,12,15,18,20)
y <- c(7.4, 9.3, 10.6, 15.4, 18.1, 22.2, 24.1, 24.8)
Sxy = sum(x * y) - 8 * mean(x) * mean(y)
Sxx = sum(x * x) - 8 * mean(x)^2
Syy = sum(y * y) - 8 * mean(y)^2
SSR = (Sxx * Syy - Sxy^2) / Sxx
SSR[1] 9.469758使用 R 求线性回归方程：
x <- c(5,6,7,10,12,15,18,20)
y <- c(7.4, 9.3, 10.6, 15.4, 18.1, 22.2, 24.1, 24.8)
df <- data.frame(x = x, y = y)
model <- lm(y ~ x, df)
model
Call:
lm(formula = y ~ x, data = df)
Coefficients:
(Intercept) x
2.463 1.206 plot(x, y)
abline(model)
如 图 9.2 所示，估计的线性回归方程为：
\(y = 2.463 + 1.206x\) \(\blacksquare\)
使用 命题 9.2，设计回归参数的假设检验和置信区间是一件非常简单的事情。
\(\beta = 0\) 是简单线性回归模型 \(Y = \alpha + \beta x + e\) 的一个重要的假设。该假设的重要性源自这样的事实，即 \(\beta = 0\) 相当于声明模型的输出均值不依赖于模型的输入，或者说没有对输入变量进行任何的回归。
为了检验：
\(H_0: \beta = 0 \quad vs. \quad H_1: \beta \ne 0\)
我们注意到，根据 命题 9.2 有：
\[ \frac{B - \beta}{\sqrt{\sigma^2 / S_{xx}}} = \sqrt{S_{xx}} \frac{B - \beta}{\sigma} \sim \mathcal{N}(0, 1) \tag{9.12}\]
同时，残差平方和 \(SS_R\) 于 \(B\) 之间相互独立，且：
\[ \frac{SS_R}{\sigma^2} \sim \chi_{n-2}^{2} \]
因此，根据 \(t\) 分布随机变量的定义，
\[ \frac{\sqrt{S_{xx}}(B - \beta) / \sigma}{\sqrt{\frac{SS_R}{\sigma^2(n-2)}}} = \sqrt{\frac{(n-2)S_{xx}}{SS_R}}(B - \beta) \sim t_{n-2} \tag{9.13}\]
也就是说，\(\sqrt{\frac{(n-2)S_{xx}}{SS_R}}(B - \beta)\) 服从自由度为 \(n-2\) 的 \(t\) 分布。因此，如果 \(H_0\) 为真（即 \(\beta = 0\)），则：
\[ \sqrt{\frac{(n-2)S_{xx}}{SS_R}}B \sim t_{n-2} \]
\(H_0: \beta = 0\) 的假设检验 \(H_0\) 在显著性水平 \(\gamma\) 下的检验为：
拒绝： \(H_0 \quad 如果 \quad \sqrt{\frac{(n-2)S_{xx}}{SS_R}} |B| \gt t_{\gamma/2, n-2}\)
接受： \(H_0 \quad 其他\)
为了计算该检验，首先计算检验统计量 \(\sqrt{(n-2)S_{XX}/SS_R}|B|\) 的值（\(v\)），然后如果如下所示的 \(p \text{-value}\) 小于给定的显著性水平则拒绝 \(H_0\)：
\(p \text{-value} = P\{|T_{n-2}| > v\} = 2P\{T_{n-2} > v\}\)
其中 \(T_{n-2}\) 服从自由度为 \(n-2\) 的 t 分布随机变量。
可以使用 R 来计算如上的假设检验。例如，如果模型的名称为 fit，那么 summary(fit) 将提供所需的 \(p \text{-value}\)。
习题 9.2 一个人声称他的汽车的燃油消耗量不依赖于汽车的行驶速度。为了检验这个假设的合理性，在不同的速度（45~70 英里/小时）测试了汽车。不同速度下的每加仑英里的测试数据如下：
| 速度 | 每加仑英里数 |
|---|---|
| 45 | 24.2 |
| 50 | 25.0 |
| 55 | 23.3 |
| 60 | 22.0 |
| 65 | 21.5 |
| 70 | 20.6 |
| 75 | 19.8 |
这些数据是否拒绝了每加仑汽油的英里数不受汽车行驶速度影响的说法？
解 9.2. 假设 \(Y\) 为汽车每加仑汽油的英里数，\(x\) 为汽车的行驶速度，并且 \(Y\) 和 \(x\) 符合简单线性回归模型：
\(Y = \alpha + \beta x + e\)
因此，题目中的假设意味着回归系数 \(\beta = 0\)。
使用 R，我们有：
x <- c(45, 50, 55, 60, 65, 70, 75)
y <- c(24.2, 25, 23.3, 22, 21.5, 20.6, 19.8)
miles <- lm(y ~ x)
miles
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
32.54 -0.17 summary(miles)
Call:
lm(formula = y ~ x)
Residuals:
1 2 3 4 5 6 7
-0.692857 0.957143 0.107143 -0.342857 0.007143 -0.042857 0.007143
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 32.54286 1.27059 25.612 1.69e-06 ***
x -0.17000 0.02089 -8.138 0.000455 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5527 on 5 degrees of freedom
Multiple R-squared: 0.9298, Adjusted R-squared: 0.9158
F-statistic: 66.23 on 1 and 5 DF, p-value: 0.0004548summary(miles) 首先给出七个数据的残差 \(y_i - (A + Bx_i)\)，其中 \(i = 1, \ldots, 7\)。接下来的几行给出了截距 \(\alpha\) 和斜率 \(\beta\) 的估计值分别为 32.54286 和 -0.17。然后，给出了这些估计值的标准误差。接着给出了用于检验回归参数为零的 \(t\)-统计量的值。例如，检验 \(\beta = 0\) 的 \(t\)-值为 -8.138。随后给出了回归参数为零的检验的 \(p \text{-value}\)，例如：\(\alpha = 0\) 的 \(p \text{-value}\) 为 \(1.69 \times 10^{-6}\)，\(\beta = 0\) 的 \(p \text{-value}\) 为 0.000455，这表明在实践中，无论显著性水平为何值，两个假设都将被拒绝。残差标准误差的值为 \(\sqrt{\frac{SS_R}{n-2}}\)。由于 \(SS_R/(n-2)\) 是 \(\sigma^2\) 的估计量，因此残差标准误差是 \(\sigma\) 的估计量。 \(\blacksquare\)
根据 式 9.13 可以很容易地得到 \(\beta\) 的置信区间估计。实际上，从 式 9.13 可以推导出，对于任意 \(a\)，其中 \(0 < a < 1\)，有
\(P \left\{ -t_{a/2, n-2} < \sqrt{\frac{(n-2)S_{xx}}{SS_R}} (B - \beta) < t_{a/2, n-2} \right\} = 1 - a\)
即：
\(P \left\{ B - \sqrt{\frac{SS_R}{(n-2)S_{xx}}} t_{a/2, n-2} < \beta < B + \sqrt{\frac{SS_R}{(n-2)S_{xx}}} t_{a/2, n-2} \right\} = 1 - a\)
于是，我们得到了以下的结果。
\(\beta\) 的置信区间
\(\beta\) 的 \(100(1 - a) \%\) 的置信区间估计是：
\(\left( B - \sqrt{\frac{SS_R}{(n-2)S_{xx}}} t_{a/2, n-2}, B + \sqrt{\frac{SS_R}{(n-2)S_{xx}}} t_{a/2, n-2} \right)\)
因为 \(\sigma^2\) 未知，所以不能直接使用 \(\frac{B - \beta}{\sqrt{\sigma^2/S_{xx}}} \sim \mathcal{N}(0,1)\) 来对 \(\beta\) 进行统计推断。相反，我们采用了 小节 9.3 中提到的 \(\sigma^2\) 的估计量 \(SS_R/(n-2)\)，这导致统计量的分布从标准正态分布变为自由度为 \(n-2\) 的 \(t\) 分布。
例 9.3 我们还可以使用 R 来获得 \(\alpha\) 和 \(\beta\) 的置信区间。如果模型的名称是 name，那么 R 命令 confint(name, level = m) 会返回模型 name 中的 \(\alpha\) 和 \(\beta\) 的 \(100m \%\) 置信区间。例如，假设我们想要计算模型 miles 的参数的 95% 置信区间。如果我们输入 confint(miles, level = 0.95)，那么 R 会返回 \(\alpha\) 和 \(\beta\) 的 95% 置信区间。
x <- c(45, 50, 55, 60, 65, 70, 75)
y <- c(24.2, 25, 23.3, 22, 21.5, 20.6, 19.8)
miles <- lm(y ~ x)
confint(miles) 2.5 % 97.5 %
(Intercept) 29.2766922 35.8090220
x -0.2236954 -0.1163046所以 \(\alpha\) 和 \(\beta\) 的 95% 置信区间分别为：\((29.2767, 35.8090)\) 和 \((-0.2237, -0.1163)\)。
术语 回归（regression）最初由 Francis Galton 在描述遗传定律时使用。Galton 认为这些定律导致了种群中的极端值“向均值回归”（regress toward the mean）。在“向均值回归”中，Galton 的意思是：在某个特征上具有极端值的人的孩子会倾向于比他们的父母具有更不极端的值。
如果我们假设在某特征上，后代 (\(Y\)) 和父代 (\(x\)) 之间存在线性回归关系，那么当回归参数 \(\beta\) 介于 0 和 1 之间时，将发生均值回归。也就是说，如果
\(E[Y] = \alpha + \beta x\)
并且 \(0 < \beta < 1\)，那么当 \(x\) 很大时，\(E[Y]\) 将小于 \(x\)；当 \(x\) 很小时，\(E[Y]\) 将大于 \(x\)。可以通过代数方法或者绘制两条直线 \(y = \alpha + \beta x\) 和 \(y = x\) 来轻松验证如上的陈述。
在直线图中我们可以发现，当 \(0 < \beta < 1\) 时，对于较小的 \(x\) 值，\(y = \alpha + \beta x\) 在 \(y = x\) 的上方，而对于较大的 \(x\) 值，则位于其下方。
例 9.4 为了演示 Galton 的均值回归理论，英国统计学家 Karl Pearson 绘制了 10 名随机选择的男孩与其父亲的身高的对比图。具体数据（以英寸为单位）如下：
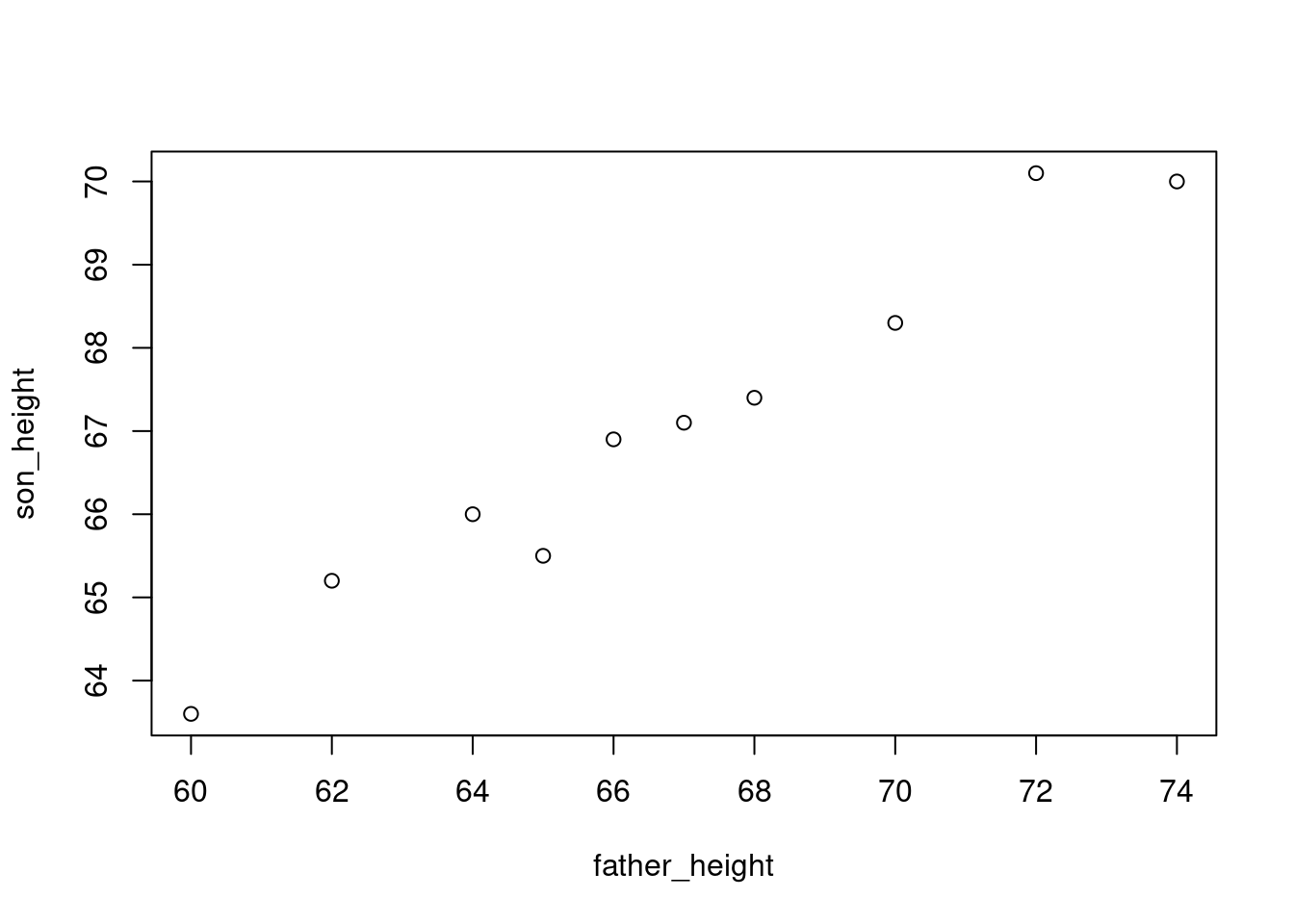
父亲的身高：60, 62, 64, 65, 66, 67, 68, 70, 72, 74
儿子的身高：63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70
如上数据的散点图如 图 9.3 所示。
father_height <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
son_height <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
plot(father_height, son_height)
注意，虽然数据表明身高较高的父亲其儿子的身高也往往较高，但也表明较高或者较低身高的父亲的儿子的身高往往比他们更“平均”——也就是说，孩子的身高有“向均值回归”的现象。
我们将通过将 均值回归 作为 备则假设 来确定上述数据是否足以证明 均值回归 的存在。也就是说，我们将使用上述数据来检验：
\(H_0: \beta \geq 1 \quad \text{vs} \quad H_1: \beta < 1\)
即：
\(H_0: \beta = 1 \quad \text{vs} \quad H_1: \beta < 1\)
根据 式 9.13，当 \(\beta = 1\) 时，检验统计量：
\(TS = \sqrt{\frac{8S_{xx}}{SS_R}}(B-1) \sim t_{8}\)
如果 \(TS = v\)，则原假设 \(H_0: \beta \ge 1\) 的 \(p \text{-value}\) 为：
\(p \text{-value} = P\{T_8 \le v\}\)
其中，\(T_8\) 为自由度为 8 的 \(t\)-分布。使用 R 来计算如上的值：
x <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
y <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
height = lm(y ~ x)
summary(height)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.6738 -0.2374 -0.0852 0.2835 0.6742
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.97681 2.20760 16.30 2.02e-07 ***
x 0.46457 0.03298 14.08 6.27e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4321 on 8 degrees of freedom
Multiple R-squared: 0.9612, Adjusted R-squared: 0.9564
F-statistic: 198.4 on 1 and 8 DF, p-value: 6.273e-07由此可知，\(\beta\) 的估计值 \(B = 0.46457\)，并且 \(\beta\) 的估计的标准误差为 0.03298，\(\beta = 0\) 时的统计检验 \(\sqrt{\frac{8S_{xx}}{SS_R}}B\) 为 14.08。因此，对于 \(H_0: \beta = 1\) 时的统计检验值 \(TS=\sqrt{\frac{8S_{xx}}{SS_R}}(B-1) = 14.08 - \frac{14.08}{0.46457} = -16.2276\)。
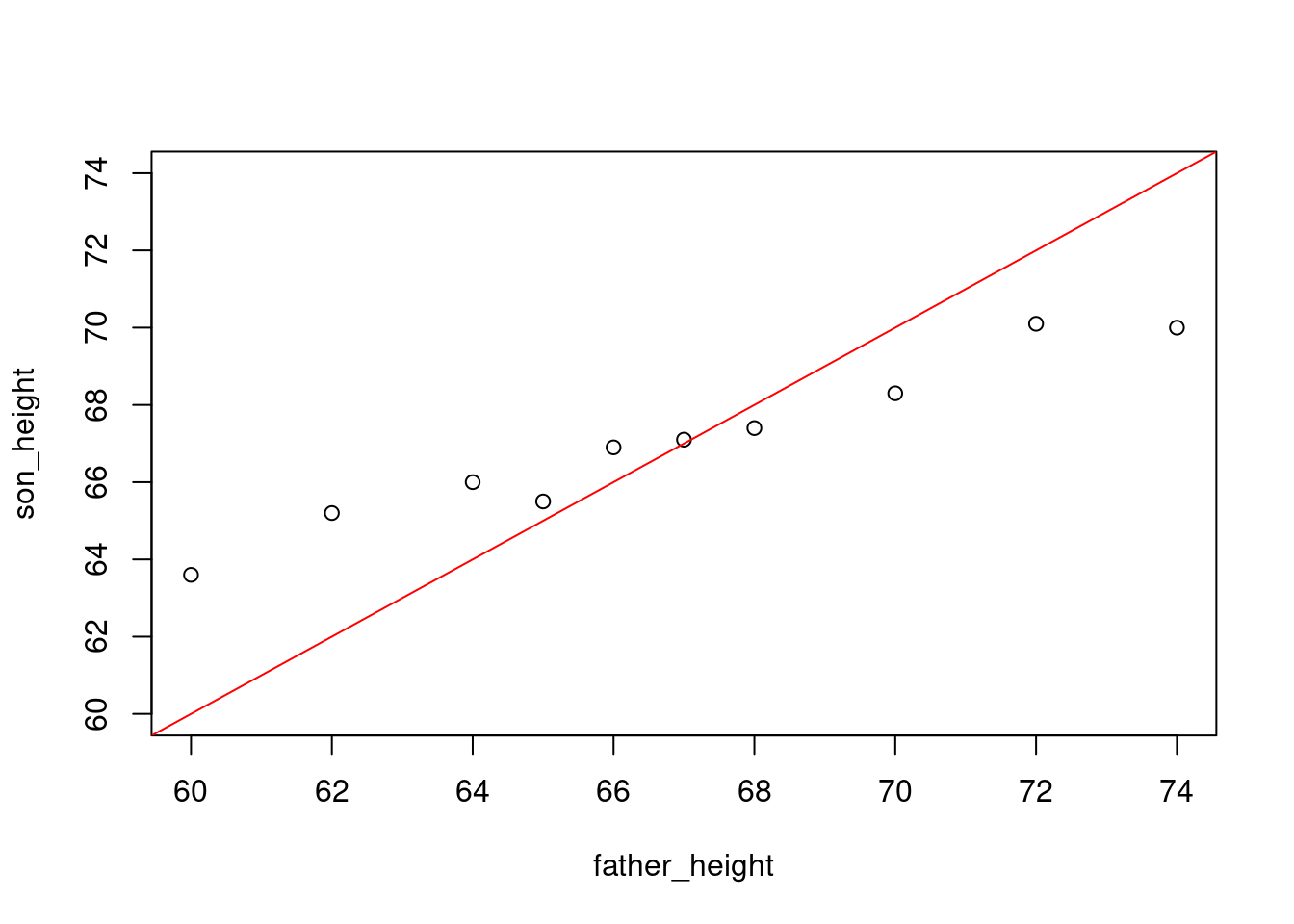
pt(-16.2276, 8)[1] 1.045567e-07因此，统计检验量的值是 -16.2276，相应的 \(p \text{-value}\) 是 \(1.045569 \times 10^{-7}\)。因此，在任何显著性水平上，原假设 $$ 将被拒绝，从而建立了均值回归。（参见 图 9.4，在 图 9.3 的散点图上增加了直线 \(y = x\)）。
father_height <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
son_height <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
plot(father_height, son_height, xlim=c(60, 74), ylim=c(60, 74))
abline(a=0, b=1, col="red")
一种现代生物学解释认为，均值回归现象大致可以解释为：后代会随机获取父母的一半的基因，因此，假设某人的身高非常高，则其后代很可能由于偶然原因拥有了更少的“高个子”基因。
尽管均值回归现象最重要的应用是关于后代与其父母的生物学特征之间的关系，但这一现象在我们拥有指向相同变量的两组数据场景时也会出现。\(\blacksquare\)
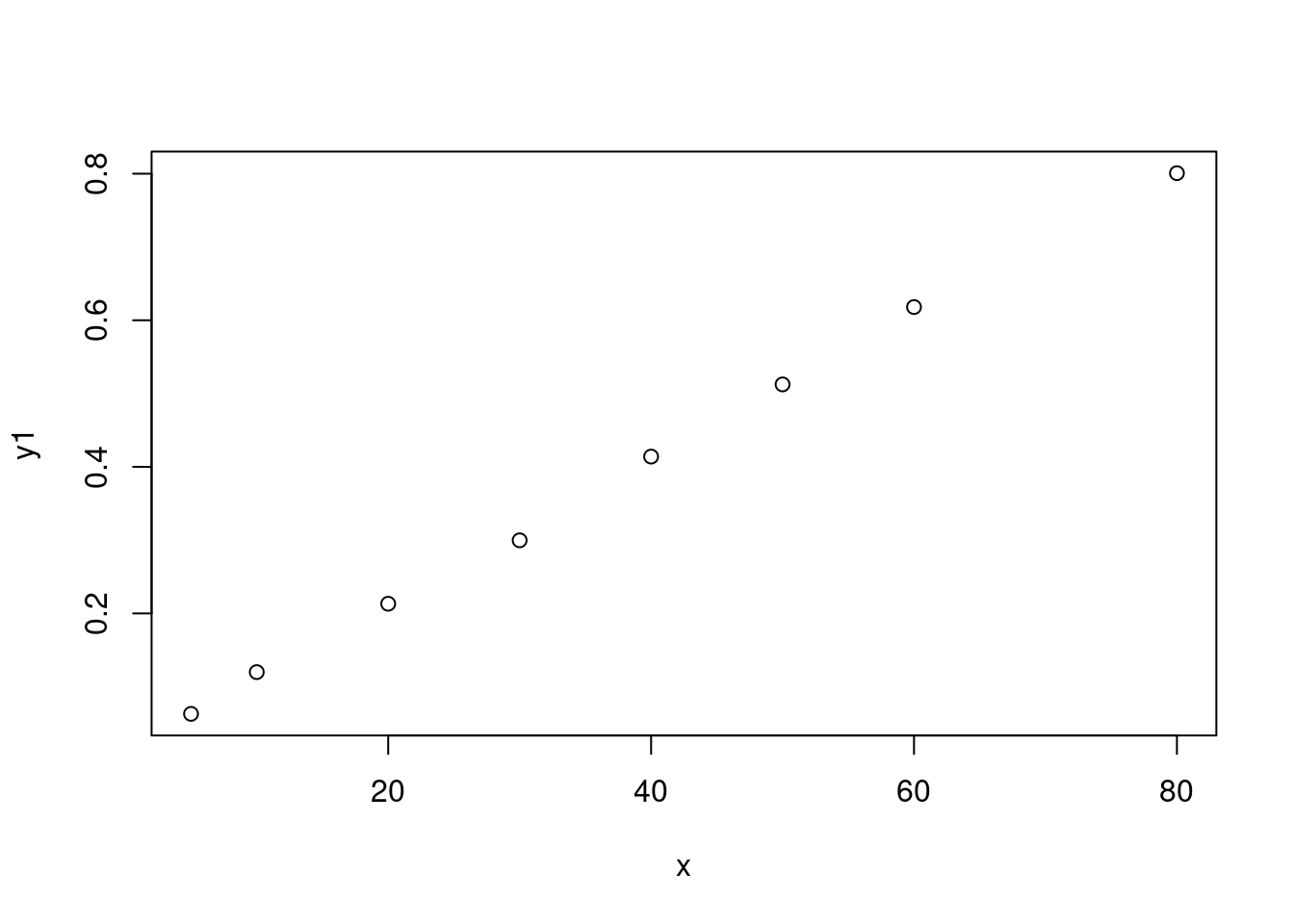
例 9.5
| 县市 | 1988 年死亡人数 | 1989 死亡人数 |
|---|---|---|
| 1 | 121 | 104 |
| 2 | 96 | 91 |
| 3 | 85 | 101 |
| 4 | 113 | 110 |
| 5 | 102 | 117 |
| 6 | 118 | 108 |
| 7 | 90 | 96 |
| 8 | 84 | 102 |
| 9 | 107 | 114 |
| 10 | 112 | 96 |
| 11 | 95 | 488 |
| 12 | 101 | 106 |
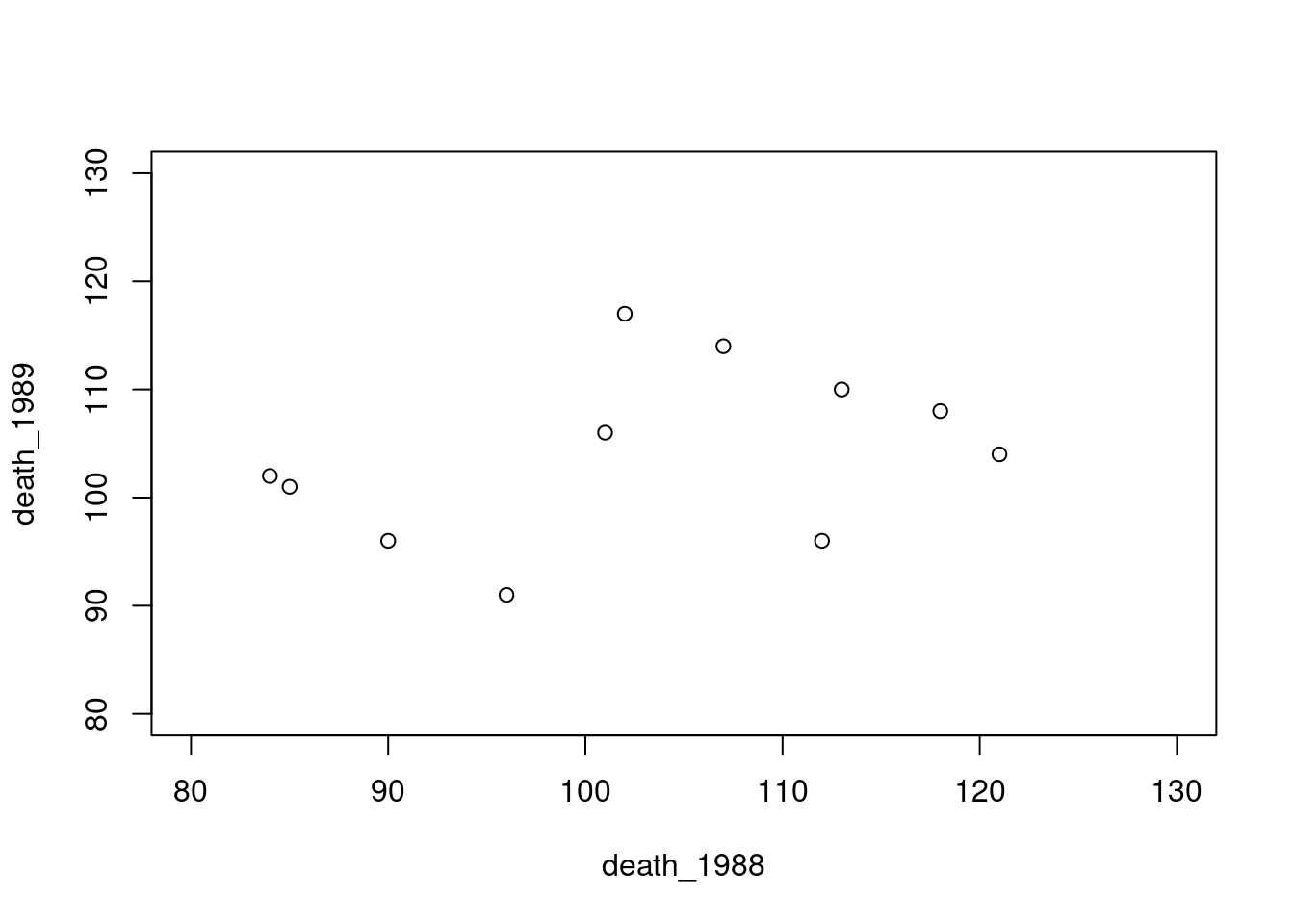
表 9.1 的数据涉及美国西北部 12 个县在 1988 年和 1989 年发生的机动车死亡人数。
death_1988 <- c(121, 96, 85, 113, 102, 118, 90, 84, 107, 112, 95, 101)
death_1989 <- c(104, 91, 101, 110, 117, 108, 96, 102, 114, 96, 488, 106)
plot(death_1988, death_1989, xlim = c(80, 130), ylim = c(80, 130))
从 图 9.5 可以看出，1989 年大多数县的死亡人数减少了，这些县在 1988 年有大量的机动车死亡人数。同样，那些在 1988 年死亡人数较少的县，1989 年的死亡人数似乎有所增加。因此，我们可以认为均值回归现象确实存在。实际上，可以用 R 计算 表 9.1 的估计回归方程：
\(y = 74.589 + 0.276x\)
这也表明，\(\beta\) 的估计值确实小于 1。
在考虑上述数据中的均值回归现象的原因时，我们必须要小心。例如，我们会很自然的假设，在 1988 年机动车死亡人数较多的县可能通过改善道路安全或让人们更多地意识到不安全驾驶的潜在危险来做出大力改进，以减少机动车死亡人数。同时，我们可能假设在 1988 年死亡人数最少的那些县可能“沾沾自喜”，并且没有做出更多的努力来进一步改善机动车的死亡人数，因此导致第二年死亡人数的增加。
尽管这种假设可能是正确的，但重要的是要认识到，即使没有任何一个县做出了任何非同寻常的举措，也可能会发生均值回归现象。事实上，很有可能在 1988 年那些死亡人数较多的县在那一年非常不幸，因此下一年的减少只是其更正常结果的回归。例如，如果抛 10 次硬币，如果出现了 9 次正面朝上，那么再抛这枚硬币 10 次，则正面向上的次数很可能会少于 9 次。同样，那些在 1988 年死亡人数较少的县在那一年可能非常“幸运”，而 1989 年的更正常结果将导致死亡人数的增加。
错误地认为均值回归是由于某种外部影响导致，但实际上均值回归只是由于统计中的随机性（chance occurs frequently）而导致的，这通常被称为 回归谬误（the regression fallacy）。\(\blacksquare\)
确定 \(\alpha\) 的置信区间和假设检验的方法与 \(\beta\) 的方法完全相同。具体而言，可利用 命题 9.2 证明：
\[ \sqrt{\frac{n(n-2)S_{xx}}{SS_R \sum_i x_i^2}} (A - \alpha) \sim t_{n-2} \tag{9.14}\]
\(\alpha\) 的置信区间估计
\(\alpha\) 的 \(100(1 - \alpha) \%\) 的置信区间为：
\[ A \pm t_{\alpha/2, n-2} \sqrt{\frac{SS_R \sum_i x_i^2}{n(n-2)S_{xx}}} \]
关于 \(\alpha\) 的假设检验可以很容易地由 式 9.14 得到，其推导过程将留作习题。
通常我们对利用数据对 \((x_i, Y_i), i = 1, \ldots, n\) 来估计 \(\alpha + \beta x_0\) 感兴趣（在给定输入 \(x_0\) 下估计平均输出）。
对于点估计量而言，那么我们自然会想到 \(A + B x_0\)，因为
\(E[A + B x_0] = E[A] + x_0 E[B] = \alpha + \beta x_0\)
所以 \(A + B x_0\) 是 \(\alpha + \beta x_0\) 的无偏估计量。
然而，如果我们需要一个置信区间，或对 \(\alpha + \beta x_0\) 进行某种假设检验，那么首先必须确定估计量 \(A + B x_0\) 的概率分布。
使用 式 9.8 中的 \(B\) 的表达式，可以得到：
\(B = c \left( \sum_{i=1}^{n} (x_i - \overline{x}) Y_i \right)\)
其中，\(c = \frac{1}{\sum_{i=1}^{n} x_i^2 - n \overline{x}^2} = \frac{1}{S_{xx}}\)
由于 \(A = \overline{Y} - B \overline{x}\)，所以
\[ \begin{align} A + B x_0 &= \frac{\sum_{i=1}^{n} Y_i}{n} - B (\overline{x} - x_0) \\ &= \sum_{i=1}^{n} Y_i \left[ \frac{1}{n} - c(x_i - \overline{x})(\overline{x} - x_0) \right] \end{align} \]
由于 \(Y_i\) 是独立的正态分布随机变量，上述等式表明 \(A + B x_0\) 可以表示为独立正态分布随机变量的线性组合，因此上述等式本身也服从正态分布。我们已经知道了 \(A + B x_0\) 的均值，现在只需要计算它的方差：
\[ \begin{align} \text{Var}(A + B x_0) &= \sum_{i=1}^{n} \left[ \frac{1}{n} - c(x_i - \overline{x})(\overline{x} - x_0) \right]^2 \text{Var}(Y_i) \\ &= \sigma^2 \sum_{i=1}^{n} \left[ \frac{1}{n^2} + c^2(x_i - x_0)^2(x_i - \overline{x})^2 - 2c(x_i - \overline{x}) \frac{(\overline{x} - x_0)}{n} \right] \\ &= \sigma^2 \left[ \frac{1}{n} + c^2(x_0 - \overline{x})^2 \sum_{i=1}^{n}(x_i - \overline{x})^2 - 2c(\overline{x} - x_0) \sum_{i=1}^{n} \frac{(x_i - \overline{x})}{n} \right] \\ &\because \sum_{i=1}^{n}{(x_i - \overline{x})^2 = \frac{1}{c} = S_{xx}}, \quad \sum_{i=1}^{n}{(x_i - \overline{x})} = 0 \\ \therefore &= \sigma^2 \left [ \frac{1}{n} + \frac{(\overline{x} - x_0)^2}{S_{xx}} \right ] \end{align} \]
于是，我们得到：
\[ A + B x_0 \sim \mathcal{N}\left ( \alpha + \beta x_0, \sigma^2 \left [ \frac{1}{n} + \frac{(\overline{x} - x_0)^2}{S_{xx}} \right ]\right ) \tag{9.15}\]
根据 命题 9.2，\(\frac{SS_R}{\sigma^2} \sim \chi_{n-2}^2\) 且其与 \(A + Bx_0\) 独立，有：
\[ \frac{A + B x_0 - (\alpha + \beta x_0)}{\sqrt{\frac{1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}} \sim t_{n-2} \tag{9.16}\]
现在，可以利用 式 9.16 得到 \(\alpha + \beta x_0\) 的置信区间估计。
\(\alpha + \beta x_0\) 的置信区间估计
在 \(100(1 - \alpha)\%\) 的置信度下，\(\alpha + \beta x_0\) 将位于：
\(A + B x_0 \pm \left(\sqrt{\frac{1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}\right)t_{\alpha/2, n-2}\)
习题 9.3 使用 例 9.4 的数据，确定在 95% 的置信度下，父亲身高为 68 英寸下的所有男性的平均身高的置信区间。
解 9.3. 我们使用 R 来计算该置信区间：
x <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
y <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
Sxy <- sum(x * y) - 10 * mean(x) * mean(y)
Sxx <- sum(x * x) - 10 * mean(x)^2
Syy <- sum(y * y) - 10 * mean(y)^2
Syy[1] 38.529SSR <- (Sxx * Syy - Sxy^2) / Sxx
SSR[1] 1.493578B <- Sxy / Sxx
A <- mean(y) - B * mean(x)
a <- sqrt((1 / 10 + (68 - mean(x))^2 / Sxx) * SSR / 8)
l <- (A + B * 68) - a * qt (0.975, 8)
u <- (A + B * 68) + a * qt (0.975, 8)
c(l,u)[1] 67.23944 67.89552所以，95% 置信区间为：\(\alpha + \beta x_0 \in (67.23944, 67.89552)\)。\(\blacksquare\)
通常情况下，估计输出的实际值比估计输出的均值更重要。例如，如果在温度为 \(x_0\) 时进行实验，那么我们可能对预测 \(Y(x_0)\) 更感兴趣（即实验的实际输出），而不是估计输出的期望 \(\text{E}[Y(x_0)] = \alpha + \beta x_0\)。另一方面，如果在温度为 \(x_0\) 时进行一系列实验，那么我们可能会更想估计输出的期望值，即 \(\alpha + \beta x_0\)。
首先，假设我们对单个值（而不是区间）感兴趣，并以此作为 \(Y(x_0)\) 的预测值，即在输入为 \(x_0\) 下的输出值。显然，\(Y(x_0)\) 的最佳预测值是其均值 \(\alpha + \beta x_0\)。实际上，这并不是那么显而易见，因为人们可能认为随机变量的最佳预测值是：
然而，由于正态分布随机变量的均值、中位数和众数相等，并且输出服从正态分布，因此此时如上的 3 种估计量并没有区别。由于 \(\alpha\) 和 \(\beta\) 是未知的，使用其估计量 \(A\) 和 \(B\) 似乎是合理的，因此可以使用 \(A + B x_0\) 作为新的输入 \(x_0\) 的新输出预测值。
假设我们现在不关心确定某个值来预测输出，而是希望找到一个预测区间，以使得在给定的置信度下，该预测区间将包含输出值。为了获得这样的区间，让 \(Y\) 表示输入为 \(x_0\) 时的输出预测值，并考虑在输出中减去其预测值的概率分布，即 \(Y - A - B x_0\)。因为，
\(Y \sim \mathcal{N}(\alpha + \beta x_0, \sigma^2)\)
并且，如 小节 9.4.4 所示，
\(A + B x_0 \sim \mathcal{N} \left( \alpha + \beta x_0, \sigma^2 \left[ \frac{1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}} \right] \right)\)
因此，由于 \(Y\) 与用于确定 \(A\) 和 \(B\) 的数据值 \(Y_1, Y_2, \ldots, Y_n\) 独立，所以 \(Y\) 与 \(A + B x_0\) 独立，因此
\(Y - A - B x_0 \sim \mathcal{N} \left( 0, \sigma^2 \left[ 1 + \frac{1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}} \right] \right)\)
即，
\[ \frac{Y - A - B x_0}{\sigma \sqrt{\frac{n+1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}}} \sim \mathcal{N}(0, 1) \tag{9.17}\]
因为 \(SS_R\) 与 \(A\) 和 \(B\) 独立（当然，也与 \(Y\) 独立），并且
\(\frac{SS_R}{\sigma^2} \sim \chi^2_{n-2}\)
于是得到，
\(\frac{Y - A - B x_0}{\sqrt{\frac{n+1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}} \sim t_{n-2}\)
因此，对于任意的 \(a\)，\(0 < a < 1\)，
\(P \left\{ -t_{a/2, n-2} < \frac{Y - A - B x_0}{\sqrt{\frac{n+1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}} < t_{a/2, n-2} \right\} = 1 - a\)
即我们构建了以下的结论。
在输入为 \(x_0\) 处时输出的预测区间
基于输入值 \(x_i\) 对应的输出值 \(Y_i\)，\(i = 1, 2, \ldots, n\)：在 \(100(1 - a)\%\) 的置信度下，\(x_0\) 处的输出值 \(Y\) 将包含在如下的区间内
\(A + B x_0 \pm t_{a/2, n-2} \sqrt{\frac{n+1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}\)
例 9.6 在 例 9.4 中，假设我们希望得到一个区间，并且我们“有 95% 的信心”认为该区间将包含父亲的身高为 68 英寸的男性的身高。简单计算后，现在得到预测区间
\(Y(68) \in 67.568 \pm 1.050\)
即，在 95% 的置信度下，父亲身高为 68 英寸的男性的身高将在 66.518 和 68.618 之间。\(\blacksquare\)
| 推断对象 | 使用的分布 |
|---|---|
| \(\beta\) | \(\sqrt{\frac{(n-2)S_{xx}}{SS_R}}(B - \beta) \sim t_{n-2}\) |
| \(\alpha\) | \(\sqrt{\frac{n(n-2)S_{xx}}{\sum x_i^2 SS_R}} (A - \alpha) \sim t_{n-2}\) |
| \(\alpha + \beta x_0\) | \(\frac{A + B x_0 - \alpha - \beta x_0}{\sqrt{\frac{1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}} \sim t_{n-2}\) |
| \(Y(x_0)\) | \(\frac{Y(x_0) - A - B x_0}{\sqrt{1 + \frac{1}{n} + \frac{(x_0 - \overline{x})^2}{S_{xx}}} \sqrt{\frac{SS_R}{n - 2}}} \sim t_{n-2}\) |
置信区间对应的是回归方程输出的平均值即 \(\alpha + \beta x_0\) （小节 9.4.4）的置信度区间，而预测区间是回归方程的输出值 \(\alpha + \beta x_0 + e\)（式 9.4）（而不是平均值）的置信区间。
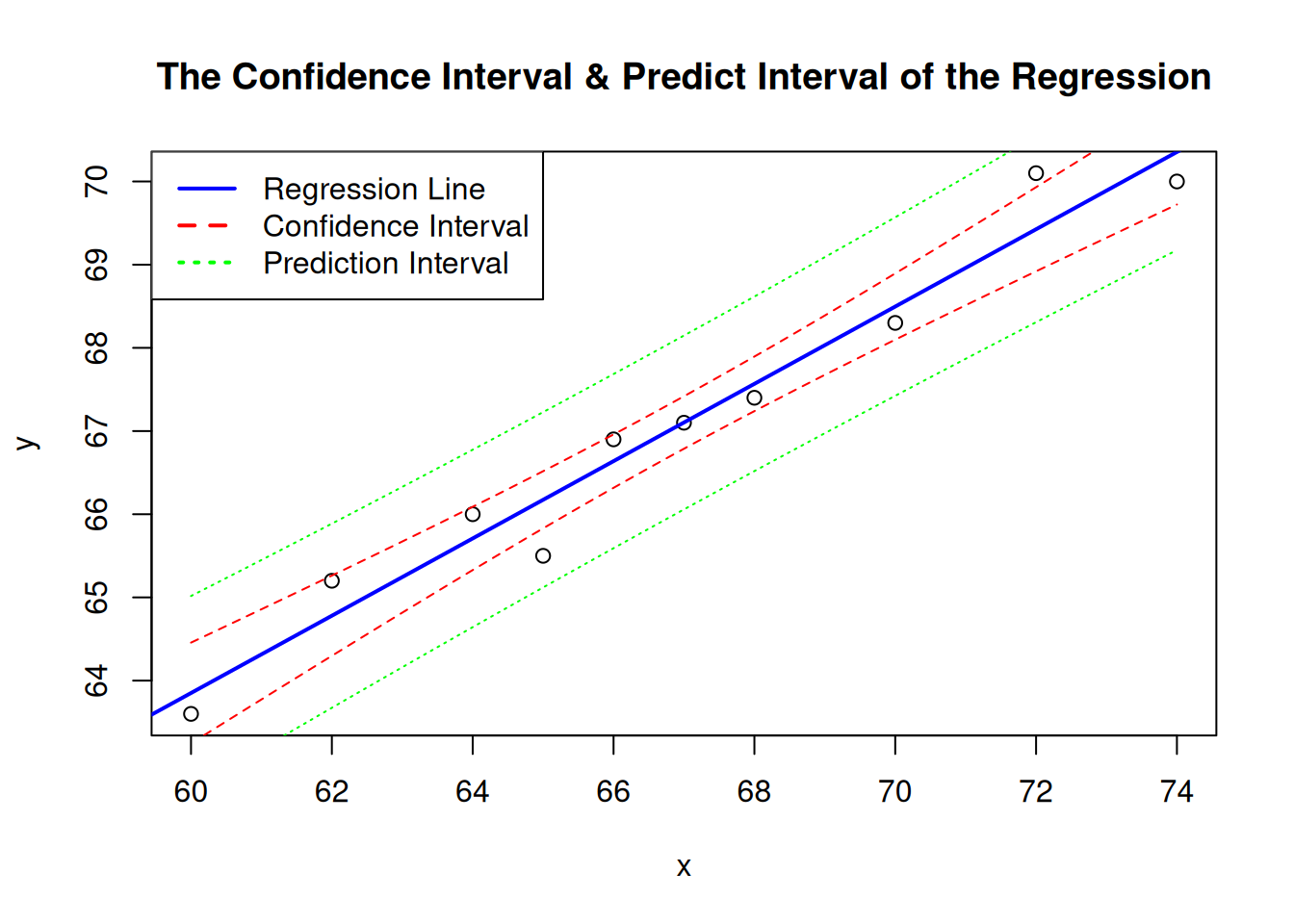
根据 表 9.2 可知，\(Y(x_0)\) 的区间比 \(\alpha + \beta x_0\) 的区间要宽。更直观的，我们可以使用 R 计算 例 9.4 的回归方程的置信区间和预测区间。
x <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
y <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
df <- data.frame(x = x, y = y)
fit <- lm(y ~ x, df)
new_x <- seq(min(x), max(x), length.out = 100)
conf_interval <- predict(fit, newdata = data.frame(x = new_x), interval = "confidence")
pred_interval <- predict(fit, newdata = data.frame(x = new_x), interval = "prediction")
plot(x, y, main = "The Confidence Interval & Predict Interval of the Regression")
abline(fit, col = "blue", lwd = 2)
lines(new_x, conf_interval[, "lwr"], col = "red", lwd = 1, lty = 2)
lines(new_x, conf_interval[, "upr"], col = "red", lwd = 1, lty = 2)
lines(new_x, pred_interval[, "lwr"], col = "green", lwd = 1, lty = 3)
lines(new_x, pred_interval[, "upr"], col = "green", lwd = 1, lty = 3)
legend("topleft", legend = c("Regression Line", "Confidence Interval", "Prediction Interval"),
col = c("blue", "red", "green"), lty = c(1, 2, 3), lwd = 2)
变异量（the amount of variation）是指一组数据中的变异性，即数据的波动或分散程度。这种波动可以是由多种因素引起的，包括个体差异、测量误差、随机误差等。在后续的翻译章节中，我们会根据具体的场景交叉使用 变异量 和 数据波动，如无特殊说明，这些指的都是一个概念。
同时，我们会避免使用 数据差异（difference） 来指代 变异量 的概念，因为在数学中，数据差异 更多指代两个数据之间的差值，因此和我们所讨论的数据的波动和分布程度并不是一个概念。
针对一组输入值 \(x_1, \ldots, x_n\)，假设我们想要测量这组输入值对应的响应值（response value） \(Y_1, \ldots, Y_n\) 之间的数据波动（或 变异量）。在统计学中，测量 \(Y_1, \ldots, Y_n\) 之间的数据波动（变异量）的标准方法为：
\(S_{YY} = \sum_{i=1}^{n} (Y_i - \overline{Y})^2\)
例如，如果所有的 \(Y_i\) 相等，那么 \(Y_i\) 都等于 \(\overline{Y}\)，所以 \(S_{YY}\) 将等于 0。
\(Y_i\) 之间的波动来源于两个因素。
让我们考虑这样一个问题：响应值的波动在多大程度上是由不同输入值引起的，又在多大程度上是由响应值的固有方差引起的（已经考虑了输入值的差异）。为了解答这个问题，我们关注到 \(SS_R\) 的定义：
\(SS_R = \sum_{i=1}^{n} (Y_i - A - Bx_i)^2\)
因此，\(SS_R\) 度量了响应变量中，除了不同输入值带来的变异量之外的、剩余的变异量。
因此，\(S_{YY} - SS_R\) 表示：响应变量中，由不同输入值能够解释的变异量。因此，我们令 \(R^2\) 表示为：响应变量中，由不同输入值能够解释的变异量比例。我们称 \(R^2\) 为 决定系数（coefficient of determination），其定义为：
\(R^2 = \frac{S_{YY} - SS_R}{S_{YY}} = 1 - \frac{SS_R}{S_{YY}}\)
解释变异量（Explained Variation）是回归分析中的一个重要概念，用于衡量回归模型中自变量能够解释的因变量的变异量。换句话说，解释变异量是由回归模型的预测结果解释的因变量的总变异的一部分。
决定系数 \(R^2\) 的取值范围在 0 和 1 之间。接近 1 的 \(R^2\) 表示响应数据的大部分波动性可以由不同的输入值来解释，而接近 0 的 \(R^2\) 则表示响应数据的波动几乎不能够由不同的输入值来解释。
例 9.7 例 9.4 中的数据揭示了父子身高之间的关系，我们可以使用 R 计算得到：
x <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
y <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
Sxy <- sum(x * y) - 10 * mean(x) * mean(y)
Sxx <- sum(x * x) - 10 * mean(x)^2
Syy <- sum(y * y) - 10 * mean(y)^2
SSr <- (Sxx * Syy - Sxy^2) / Sxx
Syy[1] 38.529SSr[1] 1.493578R2 = 1 - SSr / Syy
R2[1] 0.961235我们可以使用 R 中的 summary() 来获取 \(R^2\) 的计算结果。
x <- c(60, 62, 64, 65, 66, 67, 68, 70, 72, 74)
y <- c(63.6, 65.2, 66, 65.5, 66.9, 67.1, 67.4, 68.3, 70.1, 70)
df <- data.frame(x = x, y = y)
fit <- lm(y ~ x, df)
summary(fit)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.6738 -0.2374 -0.0852 0.2835 0.6742
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.97681 2.20760 16.30 2.02e-07 ***
x 0.46457 0.03298 14.08 6.27e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4321 on 8 degrees of freedom
Multiple R-squared: 0.9612, Adjusted R-squared: 0.9564
F-statistic: 198.4 on 1 and 8 DF, p-value: 6.273e-07根据如上结果，我们可以看到：Multiple R-squared: 0.9612，Multiple R-squared 即 \(R^2\)。换句话说，在 10 个人的身高波动中，有 96% 的身高波动是由其父亲的身高带来的（解释的），剩下的（未解释的）4% 的数据波动是由于儿子的身高波动带来的（即随机误差的方差 \(\sigma^2\)）。\(\blacksquare\)
通用用 决定系数 \(R^2\) 的值作为回归模型对数据拟合好坏的指标，\(R^2\) 值越接近 1 则表示拟合效果越好，而 \(R^2\) 值越接近 0 则表示拟合效果越差。换句话说，如果回归模型能够解释响应数据中的绝大部分波动（variation in the response data），那么就认为该模型可以较好的拟合数据。
回想一下我们在 小节 2.6 中定义的数据对 \((x_i, Y_i), i = 1, \ldots, n\) 的 样本相关系数 \(r\)：
\(r = \frac{\sum_{i=1}^{n} (x_i - \overline{x})(Y_i - \overline{Y})}{\sqrt{\sum_{i=1}^{n} (x_i - \overline{x})^2 \sum_{i=1}^{n} (Y_i - \overline{Y})^2}}\)
样本相关系数 \(r\) 提供了一种衡量 \(x\) 和 \(Y\) 之间相关性强度的方式。当 \(r\) 接近 +1 时，表示较大的 \(x\) 对应着较大的 \(Y\)，并且较小的 \(x\) 对应着较小的 \(Y\)；当 \(r\) 接近 -1 时，表示较大的 \(x\) 对应着较小的 \(Y\)，并且较小的 \(x\) 对应着较大的 \(Y\)。
在本章中，\(r = \frac{S_{xY}}{\sqrt{S_{xx} S_{YY}}}\)，根据 式 9.11 有：\(SS_R = \frac{S_{xx}S_{YY} - S_{xY}^2}{S_{xx}}\)，于是有：
\(\begin{align}r^2 &= \frac{S_{xY}^2}{S_{xx} S_{YY}} \\ &= \frac{S_{xx}S_{YY} - SS_R S_{xx}}{S_{xx}S_{YY}} \\ &= 1 - \frac{SS_R}{S_{YY}} \\ &= R^2\end{align}\)
即：
\(|r| = \sqrt{R^2}\)
因此，除了 \(r\) 的符号表示它是正相关还是负相关外，样本相关系数 和 决定系数 的平方根是一致的。\(r\) 的符号与参数 \(B\) 的符号相同。
如上的内容为 样本相关系数 提供了额外的意义。例如，如果一个数据集的 样本相关系数 \(r\) 等于 0.9，那么这意味着对于这些数据的 简单线性回归模型 可以解释 响应变量 81% 的数据波动（variation）（因为 \(R^2 = 0.9^2 = 0.81\)）。换句话说，对于响应变量的数据波动而言，81% 可以由不同的输入值来解释。
可以通过分析数据的散点图来初步确定简单线性回归模型
\(Y = \alpha + \beta x + e, \quad e \sim (0, \sigma^2)\)
是否适用于特定场景。事实上，数据散点图的分析通常足以让我们确认回归模型是否正确。当散点图本身不能确定简单线性模型是否合适时，就需要计算模型的 最小二乘估 计量 \(A\) 和 \(B\)，并分析残差 \(Y_i - (A + Bx_i)\), \(i = 1, \ldots, n\)。残差分析（analysis of residuals）需要首先对残差 正态化（normalizing）或者 标准化（standardizing），残差除以 \(\sqrt{SS_R / (n - 2)}\)（即 \(Y_i\) 的标准差的估计值，小节 9.3）得到的指标量
\(\frac{Y_i - (A + Bx_i)}{\sqrt{SS_R / (n - 2)}}, \quad i = 1, \ldots, n\)
称为 标准化残差（Standardized Residuals）。
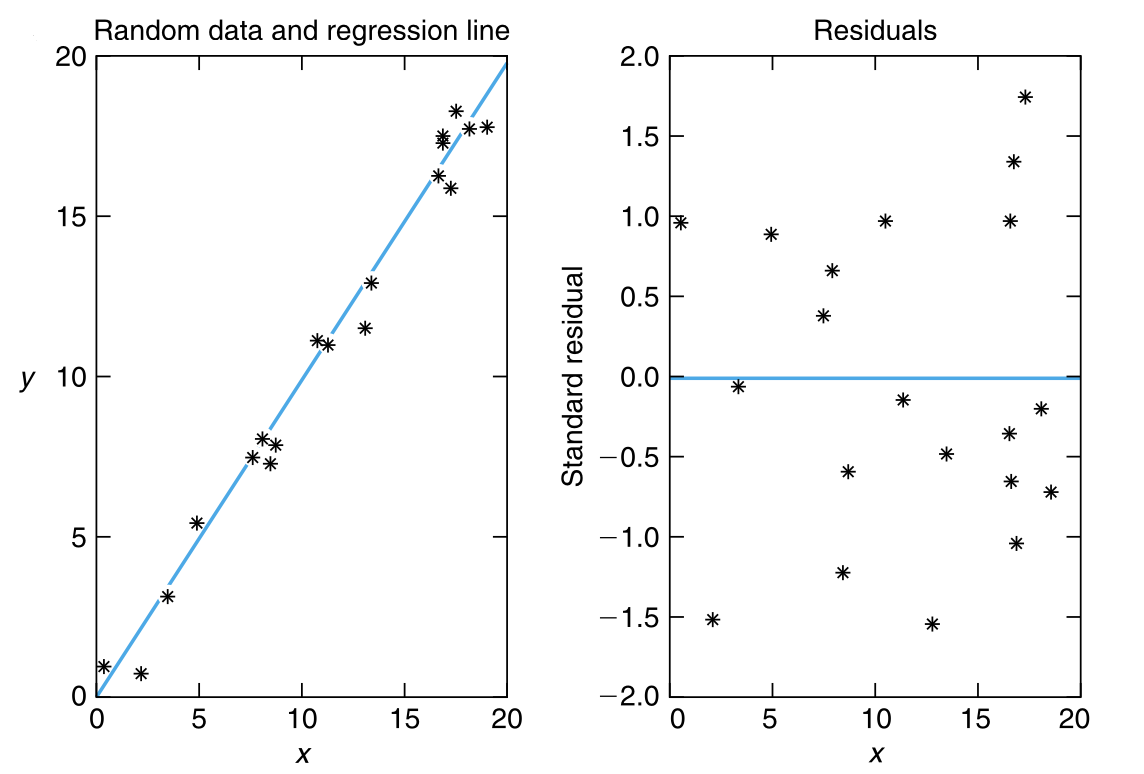
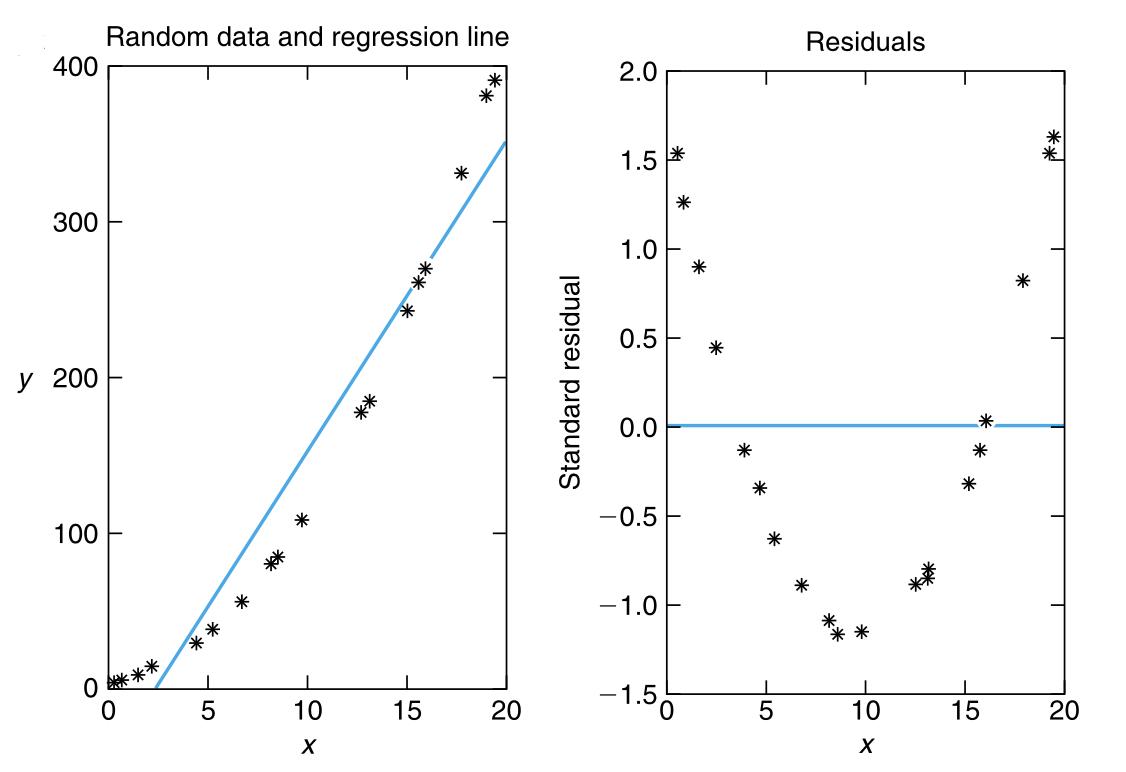
当简单回归模型正确时，标准化残差 应近似为相互独立的、标准正态分布随机变量，因此 标准化残差 应围绕 0 随机分布，且有大约 95% 的 标准化残差 应位于 \((-2, 2)\) 区间内（因为 \(P\{-1.96 < Z < 1.96\} = 0.95\)）。此外，标准化残差图不应显示出任何明显的模式（pattern）。实际上，任何明显的模式都暗示着我们需要怀疑假定的简单线性回归模型的有效性。
图 9.6 展示了三个不同的散点图及其相关的标准化残差图。图 9.6 (a) 中的散点图及其标准化残差的随机性表明线性模型的拟合比较好。图 9.6 (b) 中的残差图显示出一个明显的模式（pattern），即残差随着输入变量值的增加时呈现出先减小后增加的趋势。这通常意味着需要更高阶（不仅仅是线性）的项来描述输入和响应之间的关系。在散点图中，也体现了如上的结论。图 9.6 (c) 中的标准化残差图也显示出一种模式，即残差的值及其平方随着输入变量值的增加而增加。这通常意味着 \(Y_i\) 的方差并不是常数，而是随着输入变量值的增加而增加。
在许多情况下，响应均值（输出值的均值）明显不是输入水平（输入值）的线性函数。在这种情况下，如果可以确定输入水平和其响应均值之间的关系形式，那么有时可以通过变量变换将其转换为线性形式。例如，在某些应用中，已知信号在 \(t\) 时刻处的振幅 \(W(t)\) 近似满足：
\(W(t) \approx c e^{-dt}\)
对上式去对数运算，则可以表示为：
\(\log W(t) \approx \log c - dt\)
如果令 \(Y = \log W(t)\)，\(\alpha = \log c\)，\(\beta = -d\)，则模型 \(W(t) \approx c e^{-dt}\) 可以转换为：
\(Y = \alpha + \beta t + e\)
然后，我们可以利用最小二乘法来估计简单线性回归模型的回归参数 \(\alpha\) 和 \(\beta\)，于是 \(W(t) \approx c e^{-dt}\) 可以用如下方式来预测：
\(W(t) \approx e^{A + Bt}\)
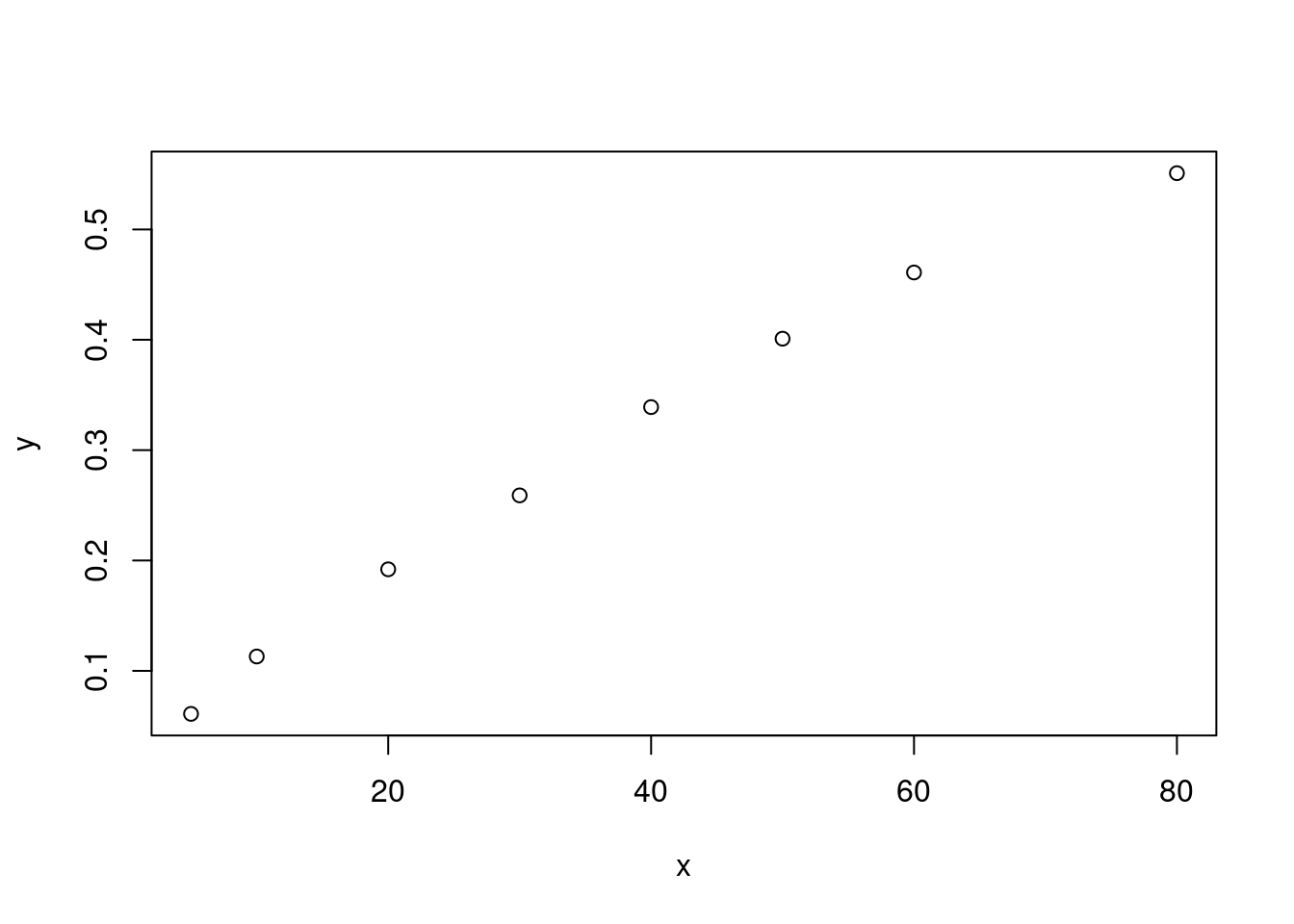
习题 9.4 下表给出了在不同温度（摄氏度）下进行实验时所使用的化学物质的百分比。使用这些数据估计：如果实验在 350 度下进行，那么需要使用的化学物质的百分比是多少？
| 温度 | 百分比 |
|---|---|
| 5° | 0.061 |
| 10° | 0.113 |
| 20° | 0.192 |
| 30° | 0.259 |
| 40° | 0.339 |
| 50° | 0.401 |
| 60° | 0.461 |
| 80° | 0.551 |
解 9.4.
x <- c(5, 10, 20, 30, 40, 50, 60, 80)
y <- c(0.061, 0.113, 0.192, 0.259, 0.339, 0.401, 0.461, 0.551)
plot(x, y)
设 \(P(x)\) 为在温度 \(10x\) 时所使用的化学物质的百分比。尽管如 图 9.7 所示，\(P(x)\) 看起来大致呈线性关系，但我们可以通过考虑 \(x\) 和 \(P(x)\) 之间的非线性关系来改进模型的拟合效果。具体而言，我们考虑以下形式的关系：
\(1 - P(x) \approx c(1 - d)^x\)
也就是说，假设在温度为 \(x\) 的实验中，所用化学物质的百分比大约以指数速率减少。对上式进行对数运算后，可以写成：
\(\log(1 - P(x)) \approx \log(c) + x \log(1 - d)\)
令：
\(\begin{align}Y &= - \log (1-P) \\ \alpha &= - \log c \\ \beta &= - \log (1-d) \end{align}\)
我们得到了一般的回归方程：
\(Y = \alpha + \beta x + e\)
为了看出数据是否支持这个模型，我们需要画出 \(x\) 和 \(- \log (1-P)\) 的散点图。表 9.3 给出了转换后的数据，图 9.8 给出了对应的散点图。
| 温度 | \(- \log (1-P)\) |
|---|---|
| 5° | 0.063 |
| 10° | 0.120 |
| 20° | 0.213 |
| 30° | 0.300 |
| 40° | 0.414 |
| 50° | 0.512 |
| 60° | 0.618 |
| 80° | 0.801 |
x <- c(5, 10, 20, 30, 40, 50, 60, 80)
y <- c(0.061, 0.113, 0.192, 0.259, 0.339, 0.401, 0.461, 0.551)
y1 <- -log(1 - y)
plot(x, y1)
使用 R 得到 \(\alpha\) 和 \(\beta\) 的最小二乘估计值（小节 9.2）：
x <- c(5, 10, 20, 30, 40, 50, 60, 80)
y <- c(0.061, 0.113, 0.192, 0.259, 0.339, 0.401, 0.461, 0.551)
y1 <- -log(1 - y)
B <- (sum(x * y1) - mean(x) * sum(y1)) / (sum(x^2) - length(x) * mean(x)^2)
A <- mean(y1) - B * mean(x)
B[1] 0.009889817A[1] 0.01544615于是得到 \(c\) 和 \(d\) 的估计值：
\(\begin{align} \hat{c} &= e^{-A} = 0.9847 \\ 1 - \hat{d} &= e^{-B} = 0.9901 \end{align}\)
最后得到估计的函数关系为：
\(\hat{P} = 1 - 0.9847 \cdot (0.9901)^x\)
如上模型的残差 \(P - \hat{P}\) 如 表 9.4 所示。
| x | P | \(\hat{P}\) | \(P - \hat{P}\) |
|---|---|---|---|
| 5 | 0.061 | 0.063 | -0.002 |
| 10 | 0.113 | 0.109 | 0.040 |
| 20 | 0.192 | 0.193 | -0.001 |
| 30 | 0.259 | 0.269 | -0.010 |
| 40 | 0.339 | 0.339 | 0.000 |
| 50 | 0.401 | 0.401 | 0.000 |
| 60 | 0.461 | 0.458 | 0.003 |
| 80 | 0.551 | 0.556 | -0.005 |
\(\blacksquare\)
在回归模型
\(Y = \alpha + \beta x + e\)
中，我们经常发现 响应变量 的方差不是常数，而是依赖于其 输入水平（input level）。如果已经知道这些方差——至少应该知道这些方差的系数——那么可以通过最小化加权平方和来估计回归参数 \(\alpha\) 和 \(\beta\)。具体来说，如果
\(\text{Var}(Y_i) = \frac{\sigma^2}{w_i}\)
那么估计量 \(A\) 和 \(B\) 应该为下式的最小化：
\(\sum_i \frac{[Y_i - (A + Bx_i)]^2}{\text{Var}(Y_i)} = \frac{1}{\sigma^2} \sum_i w_i (Y_i - A - Bx_i)^2\)
分别对 \(A\) 和 \(B\) 进行偏微分计算，然后令偏微分为 0，得到令 \(A\) 和 \(B\) 最小化的方程：
\[ \begin{align} \sum_i w_i Y_i &= A \sum_i w_i + B \sum_i w_i x_i \\ \sum_i w_i x_i Y_i &= A \sum_i w_i x_i + B \sum_i w_i x_i^2 \end{align} \tag{9.18}\]
很容易就可以求解这些方程以得到最小二乘估计量。
例 9.8 为了理解为什么应该通过最小化加权平方和而不是普通平方和来获得估计量，需要考虑以下情况。假设 \(X_1, \ldots, X_n\) 是具有均值 \(\mu\) 和方差 \(\sigma^2\) 的独立正态分布随机变量。假设 \(X_i\) 不可直接观测，而只能观测到
\(Y_1 = X_1 + \dots + X_k, \quad Y_2 = X_{k+1} + \dots + X_n, \quad k < n\)
我们如何基于 \(Y_1\) 和 \(Y_2\) 估计 \(\mu\)？
虽然 \(\mu\) 的最佳估计量显然是 \(\overline{X} = \sum_{i=1}^{n} X_i / n = (Y_1 + Y_2)/n\)，但让我们看看普通最小二乘估计量会是什么。因为
\(E[Y_1] = k\mu, \quad E[Y_2] = (n - k)\mu\)
\(\mu\) 的最小二乘估计量是使得以下表达式最小化的 \(\mu\) 的值：
\((Y_1 - k\mu)^2 + (Y_2 - [n - k]\mu)^2\)
对其求导并令其等于零，我们得到最小二乘估计量 \(\mu\)（记作 \(\hat{\mu}\)）应满足：
\(-2k(Y_1 - k\hat{\mu}) - 2(n - k)[Y_2 - (n - k)\hat{\mu}] = 0\)
即：
\([k^2 + (n - k)^2]\hat{\mu} = kY_1 + (n - k)Y_2\)
所以：
\(\hat{\mu} = \frac{kY_1 + (n - k)Y_2}{k^2 + (n - k)^2}\)
因为
\(E[\hat{\mu}] = \frac{kE[Y_1] + (n - k)E[Y_2]}{k^2 + (n - k)^2} = \frac{k^2\mu + (n - k)^2\mu}{k^2 + (n - k)^2} = \mu\)
因此，我们看到虽然普通最小二乘估计量是 \(\mu\) 的无偏估计量，但它却不是 \(\overline{X}\) 的最佳估计量。
现在，我们通过最小化加权平方和来确定 \(\mu\) 的估计量。也就是说，让我们确定 \(\mu\) 的值（记作 \(\mu_w\)）以使得以下表达式最小化：
\(\frac{(Y_1 - k\mu)^2}{\text{Var}(Y_1)} + \frac{[Y_2 - (n - k)\mu]^2}{\text{Var}(Y_2)}\)
因为
\(\text{Var}(Y_1) = k\sigma^2, \quad \text{Var}(Y_2) = (n - k)\sigma^2\)
这相当于需要选择令下式最小化的 \(\mu\)：
\(\frac{(Y_1 - k\mu)^2}{k} + \frac{[Y_2 - (n - k)\mu]^2}{n - k}\)
对其求导并令其等于零，我们得到 \(\mu_w\) 应满足：
\(\frac{-2k(Y_1 - k\mu_w)}{k} - \frac{2(n - k)[Y_2 - (n - k)\mu_w]}{n - k} = 0\)
即：
\(Y_1 + Y_2 = n\mu_w\)
所以：
\(\mu_w = \frac{Y_1 + Y_2}{n}\)
即加权最小二乘估计量实际上就是首选的估计量 \((Y_1 + Y_2) / n = \overline{X}\)。\(\blacksquare\)
假设数据是正态分布的，加权最小二乘估计量就是最大似然估计量。这是因为数据 \(Y_1, \ldots, Y_n\) 的联合概率密度为：
\(\begin{align} f_{Y_1, \ldots, Y_n}(y_1, \ldots, y_n) &= \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi (\sigma/\sqrt{w_i})}} e^{-(y_i - \alpha - \beta x_i)^2 / (2\sigma^2 / w_i)} \\ &= \frac{\sqrt{w_1 \dots w_n}}{(2\pi)^{n/2} \sigma^n} e^{-\sum_{i=1}^{n} w_i (y_i - \alpha - \beta x_i)^2 / 2\sigma^2} \end{align}\)
因此，\(\alpha\) 和 \(\beta\) 的最大似然估计量正是使的加权平方和 \(\sum_{i=1}^{n} w_i (y_i - \alpha - \beta x_i)^2\) 最小的 \(\alpha\) 和 \(\beta\) 的值。
加权平方和也可以看作是回归方程 \(Y = \alpha + \beta x + e\) 乘以 \(\sqrt{w}\)，即：
\(Y\sqrt{w} = \alpha \sqrt{w} + \beta x \sqrt{w} + e\sqrt{w}\)
在这个方程中，误差项 \(e\sqrt{w}\) 的均值为 0，且方差是常数。因此，\(\alpha\) 和 \(\beta\) 的最小二乘估计量应是使以下表达式最小的 \(A\) 和 \(B\) 的值：
\(\sum_{i} (Y_i \sqrt{w_i} - A \sqrt{w_i} - B x_i \sqrt{w_i})^2 = \sum_{i} w_i (Y_i - A - B x_i)^2\)
加权最小二乘法主要关注那些具有最大权重的数据对（会让权重最大的数据项的误差的方差最小）。
因为加权最小二乘法需要知道在任意输入水平处的响应变量的方差（至少需要知道其系数），因此加权最小二乘法可能看起来不太有用。但是，通常可以通过分析模型生成的数据来确定这些值。以下两个例子将对此进行说明。
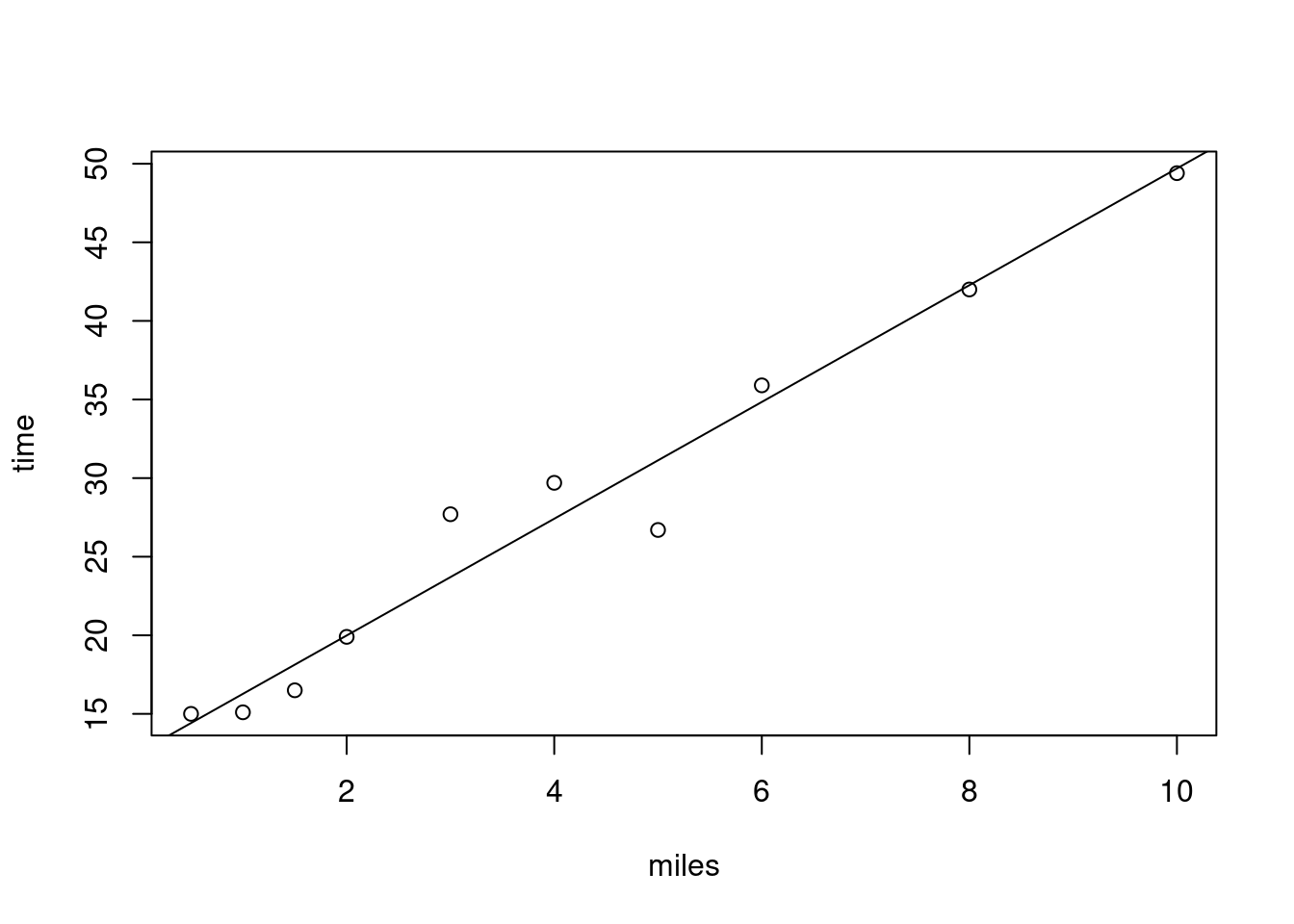
习题 9.5 下表表示某城市市区内的通勤时间。自变量或输入变量是通勤的距离。
| 通勤距离（英里） | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 通勤时间（分钟） | 15.0 | 15.1 | 16.5 | 19.9 | 27.7 | 29.7 | 26.7 | 35.9 | 42 | 49.4 |
假设通勤时间 \(Y\) 和通勤距离 \(x\) 之间的关系为线性关系：
\(Y = \alpha + \beta x + e\)
我们应如何估计 \(\alpha\) 和 \(\beta\)？
为了使用加权最小二乘法，我们需要知道 \(Y\) 的方差。现在，我们提出一个论点，即 \(\text{Var}(Y)\) 应与 \(x\) 成正比。
解 9.5. 设 \(d\) 表示一个街区的长度，于是一个通勤距离为 \(x\) 的行程将由 \(x/d\) 个街区组成。如果我们让 \(Y_i\) 表示第 \(i\) 个街区所需的时间，那么总通勤时间可以表示为：
\(Y = Y_1 + Y_2 + \dots + Y_{x/d}\)
在许多应用中，合理的假设是 \(Y_i\) 是具有相同方差的独立随机变量，因此
\(\begin{align} \text{Var}(Y) &= \text{Var}(Y_1) + \dots + \text{Var}(Y_{x/d}) \\ &= (x/d)\text{Var}(Y_1) \\ &= x\sigma^2 \end{align}\)
其中 \(\sigma^2 = \text{Var}(Y_1)/d\)。
因此，估计量 \(A\) 和 \(B\) 应该令以下表达式最小化：
\(\sum_{i} \frac{(Y_i - A - B x_i)^2}{x_i}\)
使用上面的数据，且权重为 \(w_i = 1/x_i\)，式 9.18 的最小二乘方程为：
\(\begin{align} 104.22 &= 5.34A + 10B \\ 277.9 &= 10A + 41B \end{align}\)
求解得：
\(A = 12.561, \quad B = 3.714\)
图 9.9 展示了数据点和其估计回归线 \(12.561 + 3.714x\) 的图形。对我们的解的定性分析可以知：在输入水平较小时，回归的效果最好，这主要是因为权重与输入水平成反比。
miles <- c(0.5, 1, 1.5, 2, 3, 4, 5, 6, 8, 10)
time <- c(15.0, 15.1, 16.5, 19.9, 27.7, 29.7, 26.7, 35.9, 42, 49.4)
plot(miles, time)
abline(a = 12.561, b = 3.714)
\(\blacksquare\)
例 9.9 考虑在交通繁忙的高速公路上发生的事故数量 \(Y\) 与在高速公路上行驶的车辆数量 \(x\) 之间的关系。稍微思考后，大多数人可能会认为其比较合适的关系应该为线性模型：
\(Y = \alpha + \beta x + e\)
然而，由于没有任何先验（priori）理由认为 \(\text{Var}(Y)\) 和输入水平 \(x\) 之间无关，因此我们不清楚是否可以使用普通最小二乘法来估计 \(\alpha\) 和 \(\beta\)。实际上，我们将论证：应该采用加权最小二乘法且权重为 \(1/x\)，即我们应该选择 \(A\) 和 \(B\) 以最小化
\(\sum_{i} \frac{(Y_i - A - Bx_i)^2}{x_i}\)
背后的理由是，假设 \(Y\) 近似服从泊松分布是合理的。因为我们可以想象每辆车 \(x\) 都存在一个小概率会导致事故，因此对于较大的 \(x\)，事故的数量应该近似为泊松随机变量。由于泊松随机变量的方差等于其均值，我们可以看到：
\(\begin{align} \text{Var}(Y) & \simeq E[Y] \\ &= \alpha + \beta x \\ & \simeq \beta x \end{align}\)
在响应变量的方差依赖于输入水平时，另一种常用的技术是通过适当的变换来稳定方差。例如，如果 \(Y\) 是一个均值为 \(\lambda\) 的泊松随机变量，那么可以证明（参见第 2 点），无论 \(\lambda\) 的值是多少 \(\sqrt{Y}\) 的近似方差都是 \(0.25\)。基于这一事实，可以尝试将 \(E[\sqrt{Y}]\) 建模为输入水平的线性函数，即：
\(\sqrt{Y} = \alpha + \beta x + e\)
当 \(Y\) 是具有均值 \(\lambda\) 的泊松分布时，证明 \(\text{Var}(\sqrt{Y}) \approx 0.25\)。考虑 \(g(y) = \sqrt{y}\) 在 \(\lambda\) 处的泰勒级数（Taylor series）展开。忽略二阶导数项以后的所有项，我们得到：
\[ g(y) \approx g(\lambda) + g'(\lambda)(y - \lambda) + \frac{g''(\lambda)(y - \lambda)^2}{2} \tag{9.19}\]
由于
\(g'(\lambda) = \frac{1}{2} \lambda^{-1/2}, \quad g''(\lambda) = -\frac{1}{4} \lambda^{-3/2}\)
于是，在 \(y = Y\) 处，我们得到
\(\sqrt{Y} \approx \sqrt{\lambda} + \frac{1}{2} \lambda^{-1/2}(Y - \lambda) - \frac{1}{8} \lambda^{-3/2}(Y - \lambda)^2\)
因为 \(E[Y - \lambda] = 0\) 和 \(E[(Y - \lambda)^2] = \text{Var}(Y) = \lambda\)，所以：
\(E[\sqrt{Y}] \approx \sqrt{\lambda} - \frac{1}{8\sqrt{\lambda}}\)
因此：
\((E[\sqrt{Y}])^2 \approx \lambda + \frac{1}{64\lambda} - \frac{1}{4} \approx \lambda - \frac{1}{4}\)
因此：
\(\begin{align} \text{Var}(\sqrt{Y}) &= E[Y] - (E[\sqrt{Y}])^2 \\ & \approx \lambda - \left(\lambda - \frac{1}{4}\right) \\ &= \frac{1}{4} \end{align}\)
当无法通过线性关系充分拟合响应变量 \(Y\) 和自变量 \(x\) 之间的函数关系的情况下，有时可以通过考虑多项式关系来获得合理的拟合。也就是说，可以尝试将数据集拟合到以下形式的函数关系：
\(Y = \beta_0 + \beta_1 x + \beta_2 x^2 + \cdots + \beta_r x^r + e\)
其中 \(\beta_0, \beta_1, \ldots, \beta_r\) 是需要估计的回归系数。如果数据集由 \(n\) 对 \((x_i, Y_i)\) 组成，其中 \(i = 1, \ldots, n\)，那么 \(\beta_0, \ldots, \beta_r\) 的最小二乘估计量——我们称之为 \(B_0, \ldots, B_r\)——就是使下式最小化的值：
\(\sum_{i=1}^{n} \left( Y_i - B_0 - B_1 x_i - B_2 x_i^2 - \cdots - B_r x_i^r \right)^2\)
为了确定这些估计量，我们分别求解 \(B_0 \ldots B_r\) 的偏导数，并令这些偏导数等于 0。在执行这些操作，并重新排列所得的方程之后，我们得到的最小二乘估计 \(B_0, B_1, \ldots, B_r\) 满足以下由 \(r + 1\) 个线性方程组（称为 正规方程（normal equations））成的方程组：
\[ \begin{align} \sum_{i=1}^{n} Y_i &= B_0 n + B_1 \sum_{i=1}^{n} x_i + B_2 \sum_{i=1}^{n} x_i^2 + \cdots + B_r \sum_{i=1}^{n} x_i^r \\ \sum_{i=1}^{n} x_i Y_i &= B_0 \sum_{i=1}^{n} x_i + B_1 \sum_{i=1}^{n} x_i^2 + B_2 \sum_{i=1}^{n} x_i^3 + \cdots + B_r \sum_{i=1}^{n} x_i^{r+1} \\ \sum_{i=1}^{n} x_i^2 Y_i &= B_0 \sum_{i=1}^{n} x_i^2 + B_1 \sum_{i=1}^{n} x_i^3 + B_2 \sum_{i=1}^{n} x_i^4 + \cdots + B_r \sum_{i=1}^{n} x_i^{r+2} \\ & \vdots \qquad \vdots \qquad \qquad \qquad \qquad \qquad \qquad \qquad \vdots \\ \sum_{i=1}^{n} x_i^r Y_i &= B_0 \sum_{i=1}^{n} x_i^r + B_1 \sum_{i=1}^{n} x_i^{r+1} + \cdots + B_r \sum_{i=1}^{n} x_i^{2r} \end{align} \]
在对一组数据进行多项式拟合时，通常可以通过研究散点图来确定多项式的必要阶数。我们强调，应始终使用最小可能阶数来充分描述数据的关系。例如，尽管通常可以找到一个阶数为 \(n\) 的多项式以通过所有 \(n\) 对 \((x_i, Y_i)\)，但我们很难对这种拟合寄予太大的信心。
与线性回归相比，使用多项式拟合来预测那些远离拟合数据（\(i = 1, \ldots, n\)）的 \(x_0\) 的响应值是一件更为危险的事情。多项式拟合可能只在 \(x_i\)（\(i = 1, \ldots, n\)）周围的某一区域有效，并且这个区域并不包括 \(x_0\)。
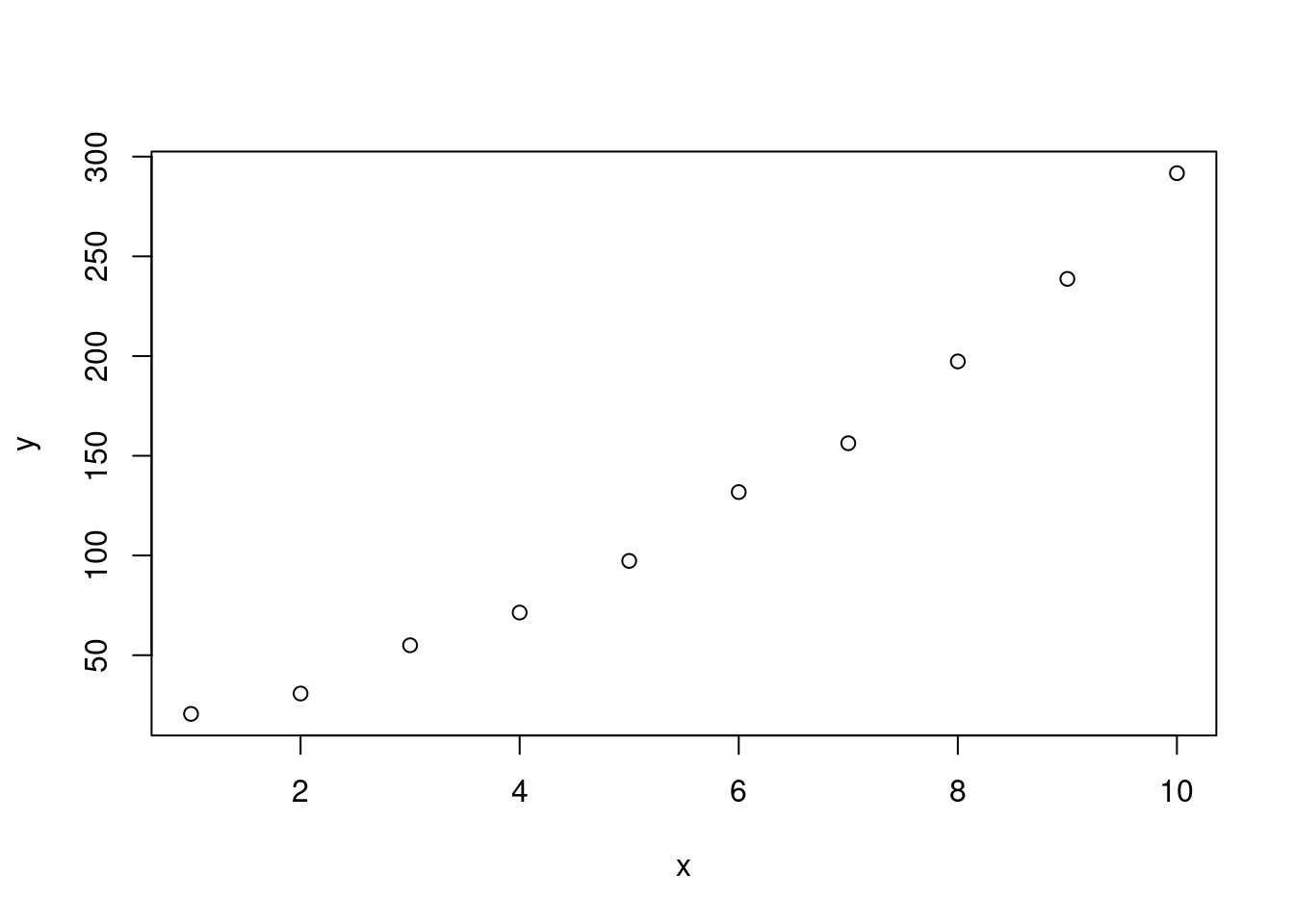
习题 9.6 为如下的数据进行多项式拟合。
| x | Y |
|---|---|
| 1 | 20.6 |
| 2 | 30.8 |
| 3 | 55.0 |
| 4 | 71.4 |
| 5 | 97.3 |
| 6 | 131.8 |
| 7 | 156.3 |
| 8 | 197.3 |
| 9 | 238.7 |
| 10 | 291.7 |
解 9.6.
x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y <- c(20.6, 30.8, 55.0, 71.4, 97.3, 131.8, 156.3, 197.3, 238.7, 291.7)
plot(x, y)
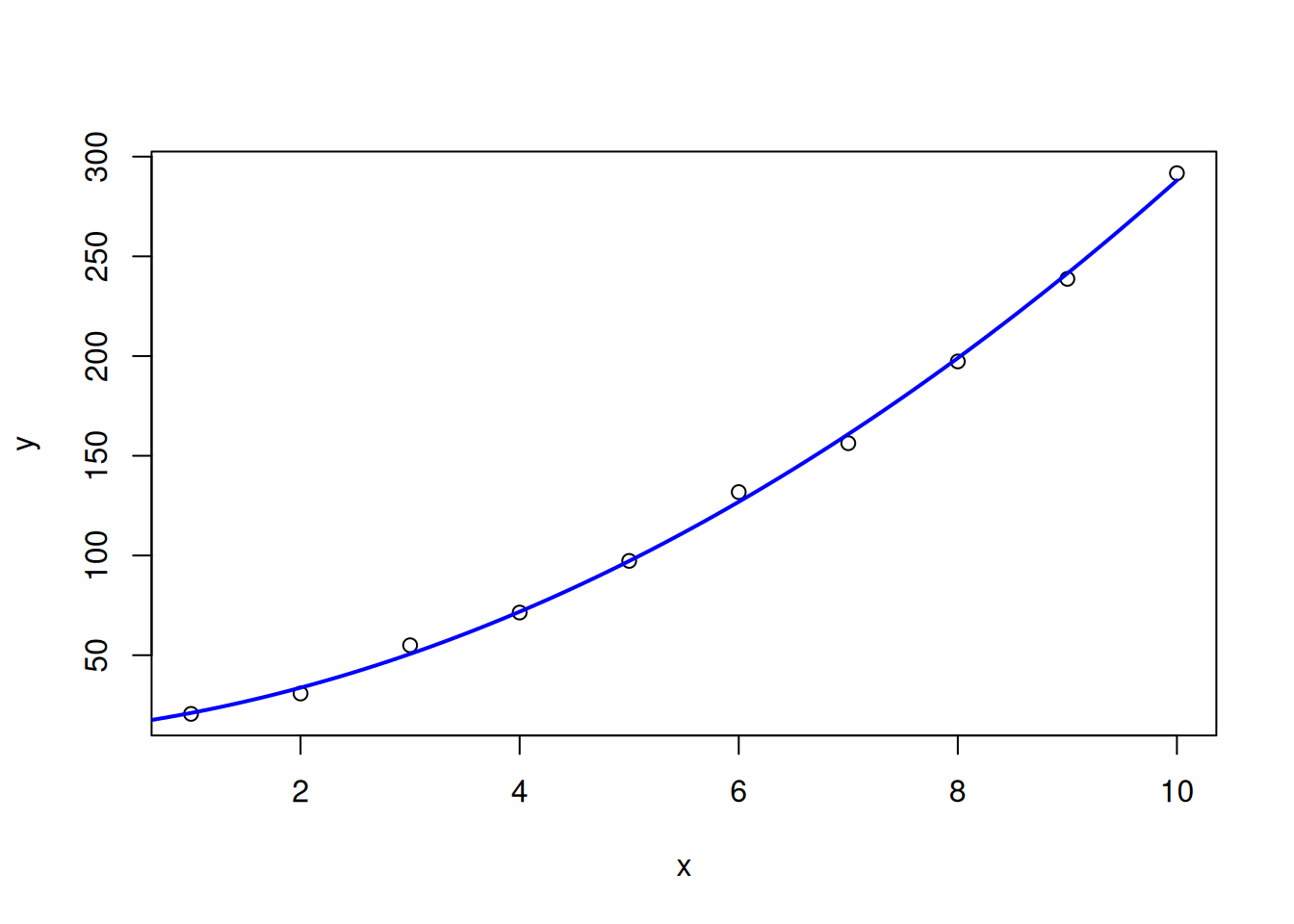
数据的散点图（图 9.10）暗示着 \(Y\) 与 \(x\) 之间存在二次关系：
\(Y = \beta_0 +\beta_1 x + \beta_2 x ^2 + e\)
\(\begin{align} \sum_{i} x_i &= 55, \quad \sum_{i} x_i^2 = 385, \quad \sum_{i} x_i^3 = 3025, \quad \sum_{i} x_i^4 = 25,333 \\ \sum_{i} Y_i &= 1291.1, \quad \sum_{i} x_i Y_i = 9549.3, \quad \sum_{i} x_i^2 Y_i = 77,758.9 \end{align}\)
所以，最小二乘估计就是如下的方程组的解：
\[ \begin{align} 1291.1 &= 10B_0 + 55B_1 + 385B_2 \\ 9549.3 &= 55B_0 + 385B_1 + 3025B_2 \\ 77758.9 &= 385B_0 + 3025B_1 + 25333B_2 \end{align} \tag{9.20}\]
解如上的方程组可以得到最小二乘估计为：
\(B_0 = 12.59326, \quad B_1 = 6.326172, \quad B_2 = 2.122818\)
因此，估计的二次回归方程为：
\(Y = 12.59 + 6.33x + 2.12x^2\)
数据的散点图和拟合的二次回归方程图如 图 9.11 所示。
x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y <- c(20.6, 30.8, 55.0, 71.4, 97.3, 131.8, 156.3, 197.3, 238.7, 291.7)
plot(x, y)
beta0 <- 12.59
beta1 <- 6.33
beta2 <- 2.12
curve(beta0 + beta1 * x + beta2 * x^2, from=0, to=10, col="red", lwd=2, add=TRUE)
\(\blacksquare\)
可以使用 R 的 lm() 实现 习题 9.6 的多项式拟合。
x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
y <- c(20.6, 30.8, 55.0, 71.4, 97.3, 131.8, 156.3, 197.3, 238.7, 291.7)
model <- lm(y ~ x + I(x^2))
summary(model)
Call:
lm(formula = y ~ x + I(x^2))
Residuals:
Min 1Q Median 3Q Max
-4.5482 -2.4869 -0.4486 2.7006 4.8739
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.6433 4.3477 2.908 0.0227 *
x 6.2971 1.8158 3.468 0.0104 *
I(x^2) 2.1250 0.1609 13.209 3.33e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.697 on 7 degrees of freedom
Multiple R-squared: 0.9987, Adjusted R-squared: 0.9984
F-statistic: 2745 on 2 and 7 DF, p-value: 7.368e-11plot(x, y)
curve(12.6433 + 6.2971 * x + 2.1250 * x^2, from=0, to=10, col="blue", lwd=2, add=TRUE)
在矩阵表示法中，式 9.20 可以表示为：
\[ \begin{bmatrix} 1291.1 \\ 9549.3 \\ 77758.9 \end{bmatrix} = \begin{bmatrix} 10 & 55 & 385 \\ 55 & 385 & 3025 \\ 385 & 3025 & 25,333 \end{bmatrix} \begin{bmatrix} B_0 \\ B_1 \\ B_2 \end{bmatrix} \]
其解为：
\[ \begin{bmatrix} B_0 \\ B_1 \\ B_2 \end{bmatrix} = \begin{bmatrix} 10 & 55 & 385 \\ 55 & 385 & 3025 \\ 385 & 3025 & 25,333 \end{bmatrix}^{-1} \begin{bmatrix} 1291.1 \\ 9549.3 \\ 77,758.9 \end{bmatrix} \]
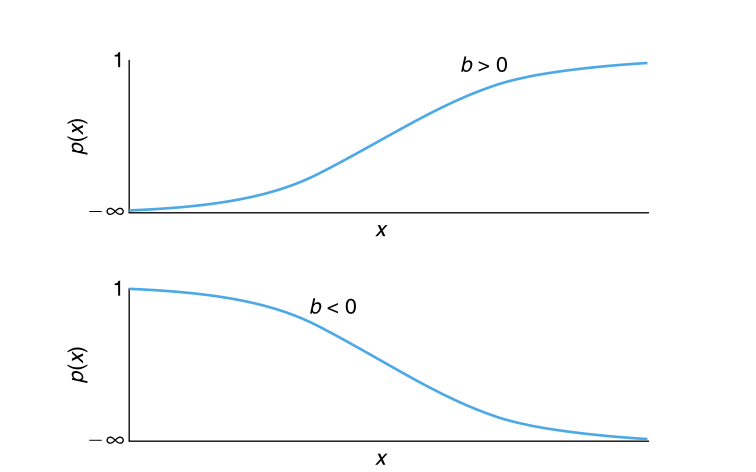
在本节中，我们考虑实验结果要么是成功要么是失败的实验。我们假设可以在不同的水平（\(x\)）执行这些实验，并且在水平 \(x\) 处实验成功的概率为 \(p(x)\)，其中 \(-\infty < x < \infty\)。如果 \(p(x)\) 具有以下形式：
\(p(x) = \frac{e^{a+bx}}{1 + e^{a+bx}}\)
那么，我们称这些实验来自于一个 逻辑回归模型（logistic regression model），而称 \(p(x)\) 为 逻辑回归函数（logistics regression function）。
图 9.12 给出了 逻辑回归函数 的图形，从图中可以看出，这些曲线呈现 S 形状。
将 \(p(x)\) 写为 \(p(x) = 1 - \left[ \frac{1}{1 + e^{a+bx}} \right]\) 并对 \(x\) 求导，得到：
\(\frac{\partial}{\partial x} p(x) = \frac{be^{a+bx}}{(1 + e^{a+bx})^2} = b \cdot p(x) [1 - p(x)]\)
因此，\(p(x)\) 的变化率取决于 \(x\)，并且在 \(p(x)\) 接近 0.5 时的那些 \(x\) 处，\(p(x)\) 的变化率最大。例如，在 \(p(x) = 0.5\) 时，\(\frac{\partial}{\partial x} p(x) = 0.25b\)，而在 \(p(x) = 0.8\) 时，\(x\) 处，\(\frac{\partial}{\partial x} p(x) = 0.16b\)。
如果我们将 \(o(x)\) 定义为实验在 \(x\) 处成功时的 赔率（小节 3.4），那么：
\(o(x) = \frac{p(x)}{1 - p(x)} = e^{a+bx}\)
因此，当 \(b > 0\) 时，赔率 随着 \(x\) 的增加而指数级增加；当 \(b < 0\) 时，赔率 随着 \(x\) 的增加而指数级减少。取 赔率 取对数运算，我们有：
\(\log(o(x)) = a + bx\)
这表明，对数赔率（log odds）——即 logit 函数——是一个线性函数：
\(\log(o(x)) = a + bx\)
逻辑回归函数的参数 \(a\) 和 \(b\) 是未知的，需要对其进行估计。可以通过最大似然法来估计逻辑回归函数的参数。也就是说，假设在 \(x_1, \ldots, x_k\) 进行实验，令 \(Y_i\)（成功时为 1，失败时为 0） 表示在 \(x_i\) 处进行实验时的实验结果。然后，使用伯努利概率密度函数（即单次试验的概率密度函数为二项概率密度函数）：
\(P(Y_i = y_i) = [p(x_i)]^{y_i} [1 - p(x_i)]^{1 - y_i} = \left( \frac{e^{a+bx_i}}{1 + e^{a+bx_i}} \right)^{y_i} \left( \frac{1}{1 + e^{a+bx_i}} \right)^{1 - y_i}, \quad y_i = 0, 1\)
因此，在 \(x_i\) 处实验结果为 \(y_i\) 的概率（对于所有 \(i = 1, \ldots, k\)） 为：
\(\begin{align} P(Y_i = y_i, i = 1, \ldots, k) &= \prod_{i} \left( \frac{e^{a+bx_i}}{1 + e^{a+bx_i}} \right)^{y_i} \left( \frac{1}{1 + e^{a+bx_i}} \right)^{1 - y_i} \\ &= \prod_{i}{\frac{(e^{a+bx_i})^{y_i}}{1+e^{a+bx_i}}} \end{align}\)
等式两边取对数得到：
\(\log\left( P\{Y_i = y_i, i = 1, \ldots, k\} \right) = \sum_{i=1}^{k} y_i(a + bx_i) - \sum_{i=1}^{k} \log \left( 1 + e^{a+bx_i} \right)\)
现在可以通过数值方法求解使得上述似然函数取得最大值的 \(a\) 和 \(b\) 的值，从而获得最大似然估计。然而，由于似然函数是非线性的，所以通常需要迭代的方法来计算最大似然估计；因此，通常需要使用专门的软件来获得逻辑回归函数的参数估计。
glm() 函数用于拟合 广义线性模型（Generalized Linear Models, GLM）。glm() 是一个非常强大的函数，可以处理各种类型的回归模型，包括线性回归、逻辑回归、泊松回归等。
可以通过 family 参数来控制 glm() 的回归类型，例如：
可以使用 R 确定逻辑回归模型中 \(a\) 和 \(b\) 的估计。可以使用 R 中的 glm(y ~ x, family = "binomial") 确定逻辑回归模型。例如，假设某个实验进行了 7 次，在 \(x = (5, 9, 13, 22, 22, 24, 30)\) 时，其对应的结果为 \((0, 1, 0, 1, 0, 1, 1)\)，其中 1 表示该实验成功，0 表示实验失败。则估计的逻辑回归方程如下：
x <- c(5, 9, 3, 12, 22, 24, 30)
y <- c(0, 1, 0, 1, 0, 1, 1)
model <- glm(y ~ x, family = "binomial")
model
Call: glm(formula = y ~ x, family = "binomial")
Coefficients:
(Intercept) x
-1.2678 0.1103
Degrees of Freedom: 6 Total (i.e. Null); 5 Residual
Null Deviance: 9.561
Residual Deviance: 8.025 AIC: 12.03在原书中，此处使用的是 glm(y ~ x)，如果没有指定 family 参数，则 glm() 实际执行的是线性回归，而不是逻辑回归。这里要特别注意。
也就是说，在逻辑回归模型 \(p(x)=\frac{e^{a+bx}}{1+e^{a+bx}}\) 中，\(a\) 和 \(b\) 的估计值分别是：-1.2678 和 0.1103。
当响应数据为二元数据时，虽然逻辑回归模型是最常用的模型，但通常也会使用其他模型。例如，在输入水平为 \(x\) 时，假设 \(p(x)\)（实验成功的概率）是一个随 \(x\) 的增加而增加的函数是合理的。在这种情况下，常常假设 \(p(x)\) 具有特定的概率分布函数。实际上，当 \(b > 0\) 时，逻辑回归模型就满足这种形式。此时，因为 \(p(x)\) 就是参数为 \(\mu = -a/b\)、\(\nu = 1/b\) 的逻辑分布随机变量的分布函数（?sec-5_9）。
可用于二元响应数据的另一种模型是 probit model，在这种模型中，假设对于某些常数 \(\alpha, \beta > 0\)，
\(p(x) = \Phi(\alpha + \beta x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\alpha + \beta x} e^{-y^2/2} dy\)
换句话说，\(p(x)\) 等于标准正态分布随机变量小于 \(\alpha + \beta x\) 的概率。
例 9.10 常见的假设是：当一个动物暴漏在剂量水平为 \(x\) 下的某化学物质时，动物是否会生病。该假设使用了阈值模型（threshold model），阈值模型认为每个动物都有一个随机阈值，当剂量水平超过该阈值时，动物就会生病。有时，可以用指数分布来作为阈值分布。例如，Freedman 和 Zeisel 在论文（From Mouse to Man: The Quantitative Assessment of Cancer Risks,” Statistical Science, 1988, 3, 1, 3–56）中的模型假设：一只暴露于 \(x\) 剂量（以 ppm 计量）的 DDT（二氯二苯基三氯乙烷，一种合成的有机氯杀虫剂，最早于 1940 年代被引入，用于控制蚊子、苍蝇等传播疾病的昆虫，并在农业中广泛用于保护农作物免受害虫侵害） 下的老鼠将会以如下的概率患上肝癌：
\(p(x) = 1 - e^{-\alpha x}, \quad x > 0\)
由于指数分布的“无记忆性”，这相当于假设：如果老鼠在接收到部分剂量 \(x\) 后仍然健康，那么剂量水平 \(x\) 带来的风险与之前没有接收到任何剂量时一样。
根据 Freedman 和 Zeisel 的研究，暴露于 250 ppm DDT 下的 111 只老鼠中，有 84 只发展成癌症。因此，可以通过以下公式估计 \(\alpha\)：
\(1 - e^{-250\hat{\alpha}} = \frac{84}{111}\)
即：
\(\hat{\alpha} = -\frac{\log(27/111)}{250} = 0.005655\) \(\blacksquare\)