11  拟合优度检验和分类数据分析

11.1 引言

我们通常需要确定某个特定的 概率模型（probabilistic model）是否适用于某个随机事件，例如我们希望能够确定是否可以用泊松分布来描述某时间段内到达商店的顾客数？我们通常通过检验给定的随机样本是否来自某个指定的概率分布来简化判断。例如，我们可能 先验（priori）地认为某工厂每天发生的工业事故数量应当是来自泊松分布的随机样本。我们可以通过观察一段时间内发生的事故数量，并用观察到的数据来检验每天发生的工业事故数服从泊松分布的假设是否合理。这种用于判断某随机事件是否满足某特定的概率模型的统计检验称之为：拟合优度检验（goodness of fit test）。

用于检验拟合优度检验的零假设——即某个样本服从某个特定的概率分布——的经典方法是：将随机变量的可能取值划分为有限的多个区域。然后确定落入每个区域的样本值的数量，并与指定概率分布下的理论数量进行比较，当这两个数据之间的差异显著时，我们将拒绝零假设，即该样本不服从我们所假设的分布。详细的检验过程将在 小节 11.2 中介绍，并且我们会假设零假设中的概率分布是完全指定的。在 小节 11.3 中，我们将介绍当零假设中的概率分布的某些参数并未指定时的分析方法，例如，零假设可能是样本分布为正态分布，但却未指定该分布的均值和方差。在 小节 11.4 和 小节 11.3 中，我们讨论了根据两种不同的特征对总体中的每个个体进行分类的情况，并展示了如何使用前述的分析方法来检验随机选择的个体的特征是否独立。我们还将演示如何检验 \(m\) 个总体都具有相同的离散概率分布的假设。最后，在 小节 11.6 中，我们将再次回到检验样本数据来自某个特定的概率分布的问题，只是我们会假设该特定分布是连续的。我们没有采用对数据离散化然后使用 小节 11.2 中的检验方法，而是会使用 Kolmogorov–Smirnov检验 直接进行检验。

11.2 概率模型的所有参数都指定时的拟合优度检验

假设有 \(n\) 个独立的随机变量 \(Y_1, Y_2, \dots, Y_n\)，其中每个变量的取值为 \(1, 2, \dots, k\)，我们希望检验如下的零假设：\(Y_j\) 的概率质量函数为 \(\{ p_i, i = 1, \dots, k \}\)。也就是说，如果用 \(Y\) 表示任意一个 \(Y_j\)，那么零假设为：

\(H_0: P\{Y = i\} = p_i, \quad i = 1, \dots, k\)

备择假设为：

\(H_1: P\{Y = i\} \neq p_i, \quad \text{对于某些} i = 1, \dots, k\)

为了检验上述假设，令 \(X_i\)（\(i = 1, \dots, k\)）表示 \(Y_j\) 等于 \(i\) 的数量。由于每个 \(Y_j\) 都独立地以概率 \(P\{Y = i\}\) 等于 \(i\)，那么原假设 \(H_0\) 为真时，\(X_i\) 服从参数为 \(n\) 和 \(p_i\) 的二项分布。因此，当原假设 \(H_0\) 为真时，

\(E[X_i] = np_i\)

因此，可以用 \((X_i - np_i)^2\) 来判断 \(p_i\) 是否确实等于 \(P\{Y = i\}\)。当 \((X_i - np_i)^2\) 比较大时，则表明 \(H_0\) 可能不成立。实际上，这种推理让我们考虑以下检验统计量：

\[ T = \sum_{i=1}^k \frac{(X_i - np_i)^2}{np_i} \tag{11.1}\]

并且，当 \(T\) 较大时，我们将拒绝零假设。

为了确定临界区，首先需要指定显著性水平 \(\alpha\)，然后确定满足下式的临界值 \(c\)：

\(P_{H_0}\{T \geq c\} = \alpha\)

也就是说，我们需要确定 \(c\)，使得当 \(H_0\) 为真时，统计量 \(T\) 大于等于 \(c\) 的概率为 \(\alpha\)。在显著性水平 \(\alpha\) 下，当 \(T \geq c\) 时，则需要拒绝原假设 \(H_0\)，否则就接受原假设。

接下来我们需要确定 \(c\) 的值。确定 \(c\) 的经典的方法是使用如下的结论：当 \(n\) 较大时，在 \(H_0\) 为真时，\(T\) 近似服从自由度为 \(k - 1\) 的卡方分布（当 \(n \rightarrow \infty\) 时，\(T\) 服从自由度为 \(k-1\) 的卡方分布）。因此，当 \(n\) 较大时，\(c\) 的取值可以是 \(\chi^2_{\alpha, k-1}\)，因此在显著性水平为 \(\alpha\) 时的近似检验为：

\(\begin{align} \text{拒绝} \quad &H_0 \quad \text{如果} T \geq \chi^2_{\alpha, k-1} \\ \text{接受} \quad &H_0 \quad \text{否则} \end{align}\)

如果观察到的统计量 \(T\) 的值为 \(t\)，那么上述检验等价于在 \(\alpha\) 值大于或等于如下的 \(p-\text{value}\) 时拒绝 \(H_0\)：

\(p-\text{value} = P_{H_0}\{T \geq t\} \approx P\{\chi^2_{k-1} \geq t\}\)

其中 \(\chi^2_{k-1}\) 是自由度为 \(k - 1\) 的卡方分布随机变量。

经验规则指出，对于 \(n\) 来说，\(n\) 需要足够大才能使得如上的检验是一个比较好的近似检验，一般而言，对于每个 \(i, i = 1,..., k\)，需要满足 \(np_i \geq 1\)，并且至少 80% 的 \(np_i\) 值应大于 5。

备注
    1. 可以展开 式 11.1 中的平方项并根据 \(\sum p_i = 1\) 和 \(\sum X_i = n\) 来更简单的计算 \(T\)（为什么可以这样计算？）：

\[ \begin{align} T &= \sum_{i=1}^k \frac{X_i^2 - 2np_i X_i + n^2 p_i^2}{np_i} \\ &= \sum_i \frac{X_i^2}{np_i} - 2 \sum_i X_i + n \sum_i p_i \\ &= \sum_i \frac{X_i^2}{np_i} - n \end{align} \tag{11.2}\]

    1. 直观上而言，依赖于 \(X_1, \dots, X_k\) 值的检验统计量 \(T\) 只有 \(k - 1\) 个自由度的原因是：有一个自由度因为线性关系 \(\sum_i X_i = n\) 而丢失了。
    1. 虽然证明 \(T\) 渐近地服从卡方分布非常复杂，但当 \(k = 2\) 时，可以很轻松的证明 \(T\) 服从卡方分布。当 \(k = 2\) 时，由于 \(X_1 + X_2 = n\)，且 \(p_1 + p_2 = 1\)，有：

\[ \begin{align} T &= \frac{(X_1 - np_1)^2}{np_1} + \frac{(X_2 - np_2)^2}{np_2} \\ &= \frac{(X_1 - np_1)^2}{np_1} + \frac{(n - X_1 - n[1 - p_1])^2}{n(1 - p_1)} \\ &= \frac{(X_1 - np_1)^2}{np_1} + \frac{(X_1 - np_1)^2}{n(1 - p_1)} \\ &= \frac{(X_1 - np_1)^2}{np_1(1 - p_1)} \quad \because \frac{1}{p} + \frac{1}{1 - p} = \frac{1}{p(1 - p)} \end{align} \]

因为 \(X_1\) 是一个二项分布随机变量，其均值为 \(np_1\)，方差为 \(np_1(1 - p_1)\)，因此，根据二项分布的正态近似性，可以得出：当 \(n\) 比较大时，\(\frac{(X_1 - np_1)}{\sqrt{np_1(1 - p_1)}}\) 近似服从标准正态分布，因此 \(\frac{(X_1 - np_1)^2}{np_1(1 - p_1)}\) 近似服从自由度为 1 的卡方分布。

习题 11.1 近年来，心理健康与身体健康之间的相关性逐渐得到人们的认可。可以使用名人的生日和去世日期之间的数据分析来进一步的研究这种相关性。为了使用这些数据，我们假设：人们对某件事情的盼望能够改善一个人的心理状态。因为生日会带来更多的关注、关爱，因此一位名人可能会对他/她的生日充满期待。如果这位名人身体不好并且濒临死亡，那么对生日的期待可能会“令他振奋，从而改善他的健康状态，并降低他在生日之前去世的概率。” 数据可能显示：名人在他/她的生日前几个月去世的可能性较小，而在生日之后的几个月去世的可能性较大。

解 11.1. 为了验证如上的假设，从《Who Was Who in America》一书中随机选取了 1251 名已故美国名人，书中记录了这些名人的出生日期和去世日期。样本数据取自 D. Phillips 的 Death Day and Birthday: An Unexpected Connection，具体的数据如 表 11.1 所示1。

表 11.1: 在生日的前后几个月中死亡数量的分布图，\(n=1251\)，\(n / 12 = 104.25\)
生日前后的月数 死亡数
6 Months Before 90
5 Months Before 100
4 Months Before 87
3 Months Before 96
2 Months Before 101
1 Month Before 86
The Month 119
1 Month After 118
2 Months After 121
3 Months After 114
4 Months After 113
5 Months After 106

如果去世日期与生日无关，那么这 1251 个人的去世日期在 12 个类别（categories）中的每个类别的可能性都是相同的。因此，我们可以检验以下的零假设：

\(H_0: p_i = \frac{1}{12}, \quad i = 1, \dots, 12\)

由于 \(np_i = 1251/12 = 104.25\)，该假设的卡方检验统计量为：

\(T = \frac{(90)^2 + (100)^2 + (87)^2 + \dots + (106)^2}{104.25} - 1251 = 17.192\)

\(p-\text{value}\) 为：

\(p-\text{value} \approx P(\chi_{11}^2 \geq 17.192) = 1 - \text{pchisq}(17.192, 11) = 0.1023232\)

检验的结果让我们对即将到来的生日是否对人的余生有影响的假设存在一些质疑。尽管这些数据不足以在 10% 的显著性水平下拒绝该假设，但它们确实表明了原假设可能是错误的。于是我们有了一个新的问题：在分析中，我们是否应该有多达 12 个数据类别，是否允许通过更少的可能类别来获得更强的检验？例如，假设我们将数据分为 4 个可能的类别：

  • 类别 1: \(-6, -5, -4\)
  • 类别 2: \(-3, -2, -1\)
  • 类别 3: \(0, 1, 2\)
  • 类别 4: \(3, 4, 5\)

也就是说，如果某人的去世日期发生在其生日前三个月内，则将其归为 类别 2。根据这种分类，我们得到如下的数据：

死亡人数
1 277
2 283
3 358
4 333

于是：\(n = 1251\)，\(\quad n/4 = 312.75\)。

\(H_0: p_i = \frac{1}{4}, \quad i = 1, 2, 3, 4\) 的检验统计量为：

\(T = \frac{(277)^2 + (283)^2 + (358)^2 + (333)^2}{312.75} - 1251 = 14.775\)

因此，由于 \(\chi_{01,3}^2 = 11.345\)，所以即使在 1% 的显著性水平下，我们也会拒绝原假设。使用 R 计算得到的 \(p-\text{value}\) 为：

\(p-\text{value} = P\{\chi_3^2 \geq 14.775\} = 1 - \text{pchisq}(14.775, 3) = 0.00201938\)

然而，如上的原假设是在观察到数据后提出的，因此上述分析可能会受到批评。确实，虽然使用一组数据来确定原假设的“正确表达方式”没有错，但再次利用这些相同的数据来检验该假设的做法是值得怀疑的。因此，要确保得出可靠的结论，按照上述的数据处理方式选择第二个随机样本似乎是必须的，并且需要在新的样本上再次检验 \(H_0: p_i = \frac{1}{4}, \quad i = 1, 2, 3, 4\)（参见 习题 3）。\(\blacksquare\)

可以使用 R 计算检验统计量和 \(p-\text{value}\)。假设 \(x = c(x_1,...,x_k)\) 是 \(k\) 个不同的类别上的对应样本数量，并且我们希望检验原假设 \(H_0: P\{i = k\} = p_i\)。可以使用如下的 R 代码：

x <- c(x1,...xk)
chisq.test(x, p=c(p1,...pk))

例如，对于 习题 11.1 而言，

x <- c(277, 283, 358, 333)
p <- c(1/4, 1/4, 1/4, 1/4)
chisq.test(x, p=p)

    Chi-squared test for given probabilities

data:  x
X-squared = 14.775, df = 3, p-value = 0.00202

习题 11.2 某荧光灯制造商对一位购货量非常大的顾客说：他们生产的这些灯泡的质量并不统一，而是按照某种方式生产的。具体而言，他们生产的每个灯泡的质量划分为 A、B、C、D、E 这 5 个等级，并且不同质量等级的灯泡的生产是独立的，同时不同等级对应的概率分别为 0.15、0.25、0.35、0.20 和 0.05。然而，该顾客认为他收到的 E 型（最低质量）灯泡太多，因此他决定花费时间和成本来确定 30 个灯泡的质量，以此来检验制造商的说法。假设他发现这 30 个灯泡中，3 个是 A 等级，6 个是 B 等级，9 个是 C 等级，7 个是 D 等级，5 个是 E 等级。那么，根据这些数据，在 5% 的显著性水平下，该顾客是否能拒绝制造商的说法？

解 11.2. 

x <- c(3, 6, 9, 7, 5)
p <- c(0.15, 0.25, 0.35, 0.20, 0.05)
chisq.test(x, p=p)
Warning in chisq.test(x, p = p): Chi-squared approximation may be incorrect

    Chi-squared test for given probabilities

data:  x
X-squared = 9.3476, df = 4, p-value = 0.05297

注意，由于每个类别中的样本量相对较小，所以 R 给出了如下警告：卡方分布对检验统计量分布的近似可能不完全准确。假设结果的准确性没有问题，则在 5% 的显著性水平下，我们不会拒绝原假设。但由于在所有高于 0.053 的显著性水平下，我们都将拒绝原假设，因此该顾客应对制造商的说法保持怀疑态度。\(\blacksquare\)

11.2.1 通过模拟确定临界区域 \(^*\)

11.3 概率模型的参数未指定时的拟合优度检验

对于概率模型 \(\{p_i, i = 1, \dots, k\}\) 而言，如果并非所有的参数都是已知的，此时我们依然可以对 原假设（null hypothesis）进行拟合优度检验。例如，对于我们在 小节 11.1 中介绍的某工厂每天事故数量的场景，现在，我们想检验该工厂每天发生的事故次数是否服参数为 \(\lambda\) 的泊松分布，其中 \(\lambda\) 是未知的。为了检验该假设，假设该工厂把 \(n\) 天内每天发生的事故次数都记录了下来，并记作 \(Y_1, \dots, Y_n\)。

要分析这些数据，我们必须首先处理这样一个问题，即 \(Y_i\) 可以有无穷多个可能的值。不过，我们可以把 \(Y_i\) 的无限种可能的取值划分为 \(k\) 个有限数量的区间，然后用 \(Y_i\) 落入的区域来解决该问题。例如，如果某天发生的事故数量为 0，则该天处于 区间 1；如果发生 1 次事故，则处于 区间 2；如果发生 2 次或 3 次事故，则处于 区间 3；如果发生 4 次或 5 次事故，则处于 区间 4；如果发生 5 次以上事故，则处于 区间 5。因此，如果该工厂每天发生的事故次数确实服从均值为 \(\lambda\) 的泊松分布，那么：

\[ \begin{align} p_1 &= P\{Y = 0\} = e^{-\lambda} \\ p_2 &= P\{Y = 1\} = \lambda e^{-\lambda} \\ p_3 &= P\{Y = 2\} + P\{Y = 3\} = \frac{e^{-\lambda} \lambda^2}{2} + \frac{e^{-\lambda} \lambda^3}{6} \\ p_4 &= P\{Y = 4\} + P\{Y = 5\} = \frac{e^{-\lambda} \lambda^4}{24} + \frac{e^{-\lambda} \lambda^5}{120} \\ p_5 &= P\{Y > 5\} = 1 - e^{-\lambda} - \lambda e^{-\lambda} - \frac{e^{-\lambda} \lambda^2}{2} - \frac{e^{-\lambda} \lambda^3}{6} - \frac{e^{-\lambda} \lambda^4}{24} - \frac{e^{-\lambda} \lambda^5}{120} \end{align} \tag{11.3}\]

在进行拟合优度检验时，我们面临的第二个难题是：均值 \(\lambda\) 的值是未知的。显然，最直接的做法是假设 \(H_0\) 为真，然后从数据中估计 \(\lambda\)——并用 \(\hat{\lambda}\) 作为 \(\lambda\) 的估计值——然后用估计量 \(\hat{\lambda}\) 来计算统计量：

\(T = \sum_{i=1}^{k} \frac{(X_i - n\hat{p_i})^2}{n\hat{p_i}}\)

其中，\(X_i\) 是落在区间 \(i\)（\(i = 1, \dots, k\) ）的 \(Y_j\) 数量，\(\hat{p_i}\) 是 \(Y_j\) 落在区间 \(i\) 的估计概率，用 \(\lambda\) 的估计量来替代 \(\hat{\lambda}\) 并代入 式 11.3 来计算 \(\hat{p_i}\)。

通常，如果原假设中含有计算概率 \(\{p_i, i = 1, \dots, k\}\) 所必需的未知参数时，我们可以使用如上的方法。假设有 \(m\) 个未知参数，并且可以用最大似然法（maximum likelihood）对其进行估计。可以证明，当 \(n\) 足够大时，在 \(H_0\) 为真时，统计量 \(T\) 近似服从自由度为 \(k - 1 - m\) 的卡方分布。换句话说，自由度会随每个需要估计的参数而减一。因此，检验为：

\(\begin{align} \text{拒绝} \quad &H_0 \quad \text{如果} \quad T \geq \chi_{\alpha, k-1-m}^2 \\ \text{接受} \quad &H_0 \quad \text{否则} \end{align}\)

另一种等价的检验方法是首先确定统计量 \(T\) 的值，记作 \(T = t\)，然后计算

\(p-\text{value} \approx P\left\{\chi^2_{k-1-m} \geq t\right\}\)

如果 \(\alpha \geq p-\text{value}\)，则拒绝原假设。

习题 11.3 假设在过去的 30 周内，每周的事故数量如下所示：

\[ \begin{array}{ccccccccccccc} 8 & 0 & 0 & 1 & 3 & 4 & 0 & 2 & 12 & 5 \\ 1 & 8 & 0 & 2 & 0 & 1 & 9 & 3 & 4 & 5 \\ 3 & 3 & 4 & 7 & 4 & 0 & 1 & 2 & 1 & 2 \end{array} \]

检验原假设：每周的事故数量服从泊松分布。

解 11.3. 由于 30 周内的事故总数为 95，泊松分布均值的最大似然估计值为：

\(\hat{\lambda} = \frac{95}{30} = 3.16667\)

因此，\(P\{Y = i\}\) 的估计值为：

\(P\{Y = i\} \stackrel{est}{=} \frac{e^{-\hat{\lambda}} \hat{\lambda}^i}{i!}\)

通过计算，我们得到：

\(\begin{align} \hat{p_1} &= 0.04214 \\ \hat{p_2} &= 0.13346 \\ \hat{p_3} &= 0.43434 \\ \hat{p_4} &= 0.28841 \\ \hat{p_5} &= 0.10164 \end{align}\)

使用数据值 \(X_1 = 6, X_2 = 5, X_3 = 8, X_4 = 6, X_5 = 5\)，我们可以使用 R 来计算检验统计量：

\(T = \sum_{i=1}^5 \frac{(X_i - 30\hat{p_i})^2}{30\hat{p_i}}\)

然后计算 \(p-\text{value}\)：

x <- c(6, 5, 8, 6, 5)
p <- c(.04214, .13346, .43434, .28841, .10164)
y <- (x - 30 * p)^2
s <- y / (30 * p)
T = sum(s)
T
[1] 21.99156
p_value <- 1 - pchisq(T, 3)
p_value
[1] 6.549552e-05

因此，我们将拒绝工厂每周发生的事故数量服从泊松分布的假设。显然，有太多周事故数量为 0，因此不能假设事故数量服从均值为 3.167 的泊松分布。\(\blacksquare\)

11.4 列联表的独立性检验

在本节中，我们将考虑这样的问题：总体中的每个成员都可以根据两个不同的特征（characteristics）进行分类——我们将这些特征分别记作 \(X-\text{特征}\) 和 \(Y-\text{特征}\)。假设 \(X-\text{特征}\) 有 \(r\) 个可能的取值，\(Y-\text{特征}\) 有 \(s\) 个可能的取值。对于 \(i = 1, \dots, r\)，\(j = 1, \dots, s\)，定义

\(P_{ij} = P\{X = i, Y = j\}\)

也就是说，\(P_{ij}\) 表示随机选择的一个总体成员具有 \(X-\text{特征}\) \(i\) 和 \(Y-\text{特征}\) \(j\) 的概率。假设总体中的不同成员之间是独立的，令

\(p_i = P\{X = i\} = \sum_{j=1}^{s} P_{ij}, \quad i = 1, \dots, r\)

\(q_j = P\{Y = j\} = \sum_{i=1}^{r} P_{ij}, \quad j = 1, \dots, s\)

也就是说，\(p_i\) 是某个总体成员具有 \(X-\text{特征}\) \(i\) 的概率，\(q_j\) 是其具有 \(Y-\text{特征}\) \(j\) 的概率。

我们希望检验这样的一个假设：总体成员的 \(X-\text{特征}\) 和 \(Y-\text{特征}\) 是相互独立的。即，我们希望检验

\[ \begin{align} H_0: & P_{ij} = p_i q_j, \quad \forall \, i = 1, \dots, r; j = 1, \dots, s \\ \qquad & vs \\ H_1: & P_{ij} \neq p_i q_j, \quad \exists i, j \quad i = 1, \dots, r; j = 1, \dots, s \end{align} \]

假设我们从总体中抽取了 \(n\) 个样本，其中有 \(N_{ij}\) 个样本同时具有 \(X-\text{特征}\) \(i\) 和 \(Y-\text{特征}\) \(j\)，\(i = 1, \dots, r; j = 1, \dots, s\)。

由于原假设中未指定的 \(p_i\) 和 \(q_j\)，我们必须估计他们，因为

\(N_i = \sum_{j=1}^{s} N_{ij}, \quad i = 1, \dots, r\)

表示样本中具有 \(X-\text{特征}\) \(i\) 的样本数量，\(p_i\) 的估计值（事实上是最大似然估计值）为

\(\hat{p_i} = \frac{N_i}{n}, \quad i = 1, \dots, r\)

同样地，令

\(M_j = \sum_{i=1}^{r} N_{ij}, \quad j = 1, \dots, s\)

表示样本中具有 \(Y-\text{特征}\) \(j\) 的样本数量，则 \(q_j\) 的估计值为

\(\hat{q_j} = \frac{M_j}{n}, \quad j = 1, \dots, s\)

乍一看，我们似乎需要使用数据来估计 \(r + s\) 个参数。然而，由于 \(p_i\) 的和与 \(q_j\) 的和都必须为 1，也就是说，\(\sum_{i=1}^{r} p_i = \sum_{j=1}^{s} q_j = 1\)。所以，我们实际上只需要估计 \(r-1\) 个 \(p_i\) 和 \(s-1\) 个 \(q_j\)。例如，如果 \(r = 2\)，因为 \(p_2 = 1 - p_1\)，所以一旦估计了 \(p_1\)，就可以自动推导出 \(p_2\)。因此，我们实际上需要估计 \(r - 1 + s - 1 = r + s - 2\) 个参数，由于每个总体成员都有 \(k = rs\) 个不同的可能取值，在 \(n\) 较大的情况下，检验统计量将近似服从自由度为 \(rs - 1 - (r + s - 2) = (r-1)(s-1)\) 的卡方分布。

所以，当 \(H_0\) 为真时，

\(E[N_{ij}] = nP_{ij} = np_iq_j\)

因此，检验统计量 \(T\) 的定义为

\(T = \sum_{j=1}^{s} \sum_{i=1}^{r} \frac{(N_{ij} - n \hat{p_i} \hat{q_j})^2}{n \hat{p_i} \hat{q_j}} = \sum_{j=1}^{s} \sum_{i=1}^{r} \frac{N_{ij}^2}{n \hat{p_i} \hat{q_j}} - n\)

如果检验统计量的值为 \(T = t\)，则相应的 \(p-\text{value}\)：

\(\begin{align} p-\text{value} &= P_{H_0}(T \geq t) \\ &\approx P\{\chi^2_{(r-1)(s-1)} \gt t\} \\ &= 1 - \text{pchisq}(t, (r-1)(s-1)) \end{align}\)

习题 11.4 我们随机选取了 300 个人作为样本，并对其按照性别和政治派别（民主党人、共和党人、无党派人士）进行分类。如下的列联表展示了所得到的数据。

\(i\)/\(j\) 民主党人 共和党人 无党派人士 总计
女性 68 56 32 156
男性 52 72 20 144
总计 120 128 52 300

例如，列联表表明，在 300 人的样本中，有 68 名女性是民主党，56 名女性是共和党，32 名女性是无党派人士；即 \(N_{11}=68\)，\(N_{12}=56\)，\(N_{13}=32\)。类似地，\(N_{21}=52\)，\(N_{22}=72\)，\(N_{23}=20\)。

利用这些数据检验随机选取的一个人的性别和政治派别是独立的这一假设。

解 11.4. 根据上述数据，我们得到 \(n\hat{p_i}\hat{q_j}=\frac{N_iM_j}{n}\) 的 6 个值如下：

\(\frac{N_{1}M_{1}}{n}=\frac{156\times120}{300}=62.40\) \(\frac{N_{1}M_{2}}{n}=\frac{156\times128}{300}=66.56\) \(\frac{N_{1}M_{3}}{n}=\frac{156\times52}{300}=27.04\) \(\frac{N_{2}M_{1}}{n}=\frac{144\times120}{300}=57.60\) \(\frac{N_{2}M_{2}}{n}=\frac{144\times128}{300}=61.44\) \(\frac{N_{2}M_{3}}{n}=\frac{144\times52}{300}=24.96\)

因此，检验统计量的值为：

\(\begin{align} TS&=\frac{(68 - 62.40)^{2}}{62.40}+\frac{(56 - 66.56)^{2}}{66.56}+\frac{(32 - 27.04)^{2}}{27.04}+\frac{(52 - 57.60)^{2}}{57.60} \\ &+\frac{(72 - 61.44)^{2}}{61.44}+\frac{(20 - 24.96)^{2}}{24.96}\\ &=6.433 \end{align}\)

\((r - 1)(s - 1)=2\)，我们使用 R 来获得 \(p-\text{value}\)。

p_value <- 1 - pchisq(6.433, 2)
p_value
[1] 0.04009515

因此，在 5% 的显著性水平下，我们将拒绝性别和政治派别是独立的原假设。

注记

我们可以直接使用 R 中的卡方检验函数来进行检验。

women <- c(68, 56, 32)
men <- c(52, 72, 20)
data <- matrix(c(women, men), nrow = 2, byrow = TRUE)
colnames(data) <- c("Democrat", "Republican", "Independent")
rownames(data) <- c("Women", "Men")

data
      Democrat Republican Independent
Women       68         56          32
Men         52         72          20
chisq.test(data)

    Pearson's Chi-squared test

data:  data
X-squared = 6.4329, df = 2, p-value = 0.0401

\(\blacksquare\)

习题 11.5 一家公司每天会安排三个不同的班次工人来操作四台机器。下面的列联表展示了在六个月的时间里的机器故障数据。

表 11.2: 机器故障数
班次 机器 A 机器 B 机器 C 机器 D 总计
班次 1 10 12 6 7 35
班次 2 10 24 9 10 53
班次 3 13 20 7 10 50
每台机器总计 33 56 22 27 138

假设我们希望确定某台机器在特定班次发生故障的概率是否受该班次的影响。换句话说，对于任意一次故障，我们希望检验导致故障的机器和故障发生的班次之间是否独立。

解 11.5. 根据计算，我们得出检验统计量的值为 1.8148。因此，\(p-\text{value}\) 为：

p_value <- 1 - pchisq(1.9148, 6)
p_value
[1] 0.9273652

因此，我们将接受导致故障的机器和故障发生的班次是独立的假设。\(\blacksquare\)

11.5 具有固定边缘总和的列联表的独立性检验

在 习题 11.4 中，我们确定了：在特定人群中性别和政治派别的相关性。为了检验我们的原假设，我们首先从该人群中选择了一个随机样本，然后记录了样本的 特征（characteristics）。

然而，我们收集数据的另一种方式是：预先确定样本中男性和女性的数量，然后从男性和女性人群中选择对应大小的随机样本。也就是说，样本中的男性和女性的数量并不是由随机抽取而决定，而是提前确定他们的数量。因为这样做会导致样本中的男性样本总数和女性样本总数都有固定的特定值，所以我们通常称由此得到的列联表具有固定的边缘（fixed margins）。

事实证明，即便使用以上的规则来收集数据，小节 11.4 中给出的假设检验仍然可以用来检验两个特征的独立性。检验统计量仍然是

\(TS=\sum_{i}\sum_{j}\frac{(N_{ij}-\hat{e}_{ij})^{2}}{\hat{e}_{ij}}\)

  • \(N_{ij}\) 是样本中同时具有 \(X-\text{特征}\) \(i\) 和 \(Y-\text{特征}\) \(j\) 的样本数量
  • \(N_{i}\) 是样本中具有 \(X-\text{特征}\) \(i\) 的样本数量
  • \(M_{j}\) 是样本中具有 \(Y-\text{特征}\) \(j\) 的样本数量
  • \(\hat{e}_{ij}=n\hat{p}_{i}\hat{q}_{j}=\frac{N_{i}M_{j}}{n}\) ，其中 \(n\) 是样本的总大小。

此外，当原假设 \(H_0\) 为真时， \(TS\) 仍然近似具有自由度为 \((r - 1)(s - 1)\) 的卡方分布。这里的量 \(r\) 和 \(s\) 分别指的是 \(X-\text{特征}\) 和 \(Y-\text{特征}\) 可能取值的数量。换句话说，独立性假设检验与某个特征的边缘总和是预先固定的还是由整个总体的随机样本产生的无关。

习题 11.6 随机选取了 20000 名不吸烟者和 10000 名吸烟者，并对他们进行了为期 10 年的跟踪调查。以下数据显示了在这段时间内患肺癌的人数。

吸烟者数量 不吸烟者数量 总计
患肺癌数量 62 14 76
未患肺癌数量 9938 19986 29924
总计 10000 20000 30000

在 1% 的显著性水平下检验吸烟与肺癌是否独立的假设。

解 11.6. 当吸烟和肺癌无关时，每个 \(ij\) 单元格中预期人数的估计值为：

\(\hat{e}_{11}=\frac{(76)(10000)}{30000}=25.33\)

\(\hat{e}_{12}=\frac{(76)(20000)}{30000}=50.67\)

\(\hat{e}_{21}=\frac{(29924)(10000)}{30000}=9974.67\)

\(\hat{e}_{22}=\frac{(29924)(20000)}{30000}=19949.33\)

因此，检验统计量的值为：

\(\begin{align*} TS&=\frac{(62 - 25.33)^{2}}{25.33}+\frac{(14 - 50.67)^{2}}{50.67}+\frac{(9938 - 9974.67)^{2}}{9974.67} \\ &+\frac{(19986 - 19949.33)^{2}}{19949.33}\\ &=53.09 + 26.54 + 0.13 + 0.07 = 79.83 \end{align*}\)

因此，\(p-\text{value}\approx P(\chi_{1}^{2}>79.83)=1-\text{pchisq}(79.83,1)\approx0\) 。

所以，在任何显著性水平下，随机选取的一个人患肺癌与否与这个人是否吸烟无关的原假设都会被拒绝。

接下来，我们将介绍如何使用本节的计算框架来检验 \(m\) 个离散总体分布是否相等的假设。考虑 \(m\) 个独立的总体，每个总体的成员取值为 \(1,\ldots,n\)。假设从总体 \(i\) 中随机选取的一个成员的值为 \(j\) 的概率为 \(p_{i,j}\) ，其中 \(i = 1,\ldots,m\)，\(j = 1,\ldots,n\)。检验如下的原假设：

\(H_0：\forall j = 1,\ldots,n, \quad p_{1,j}=p_{2,j}=p_{3,j}=\cdots=p_{m,j}\)

首先考虑由这 \(m\) 个总体的所有成员组成的 超总体（superpopulation）。该 超总体 的任何成员都可以根据两个 特征 进行分类。第一个特征指定成员来自 \(m\) 个总体中的哪一个，第二个特征指定其取值。于是，\(m\) 个总体的分布都相等的假设就变成了如下的假设：对于每个取值而言，该取值在 \(m\) 个总体中的每一个中的比例都是相同的。但这完全等同于：从超总体中随机选取的一个成员的两个特征是独立的。

因此，我们可以通过从每个总体中随机选取样本成员来检验 \(H_0\)。如果我们用 \(M_i\) 表示从总体 \(i\) 中抽取的样本大小，用 \(N_{i,j}\) 表示该样本中取值等于 \(j\) 的数量，其中 \(i = 1,\ldots,m\)，\(j = 1,\ldots,n\)，那么我们可以通过检验如下的列联表中特征的独立性来检验 \(H_0\)。

取值 总体 1 总体 2 \(\cdots\) 总体 \(i\) \(\cdots\) 总体 \(m\) 总计
1 \(N_{1,1}\) \(N_{2,1}\) \(\cdots\) \(N_{i,1}\) \(\cdots\) \(N_{m,1}\) \(N_1\)
2
\(\vdots\)
\(j\) \(N_{1,j}\) \(N_{2,j}\) \(\cdots\) \(N_{i,j}\) \(\cdots\) \(N_{m,j}\) \(N_j\)
\(\vdots\)
\(n\) \(N_{1,n}\) \(N_{2,n}\) \(\cdots\) \(N_{i,n}\) \(\cdots\) \(N_{m,n}\) \(N_n\)
总计 \(M_1\) \(M_2\) \(\cdots\) \(M_i\) \(\cdots\) \(M_m\)

注意，\(N_j\) 表示样本中取值为 \(j\) 的成员的数量。

习题 11.7 最近的一项研究报告称，他们从四个不同的国家随机选取了500名（每个国家随机选择 500 名）女性办公室职员进行调研。其中一个问题就是：她们在工作中是否经常受到言语或性虐待，并得到了如下数据。

国家 受虐待的人数
澳大利亚 28
德国 30
日本 51
美国 55

基于这些数据，这些国家中经常在工作中感到受虐待的女性办公室职员的比例相同这一说法是否合理？

解 11.7. 将上述数据表示成如下的列联表：

国家 1 国家 2 国家 3 国家 4 总计
受到虐待 28 30 51 55 171
未受虐待 472 470 442 445 1829
总计 500 500 500 500 2000

可以通过检验上述列联表中的独立性来检验原假设。使用 R 语言得到检验统计量的值为 \(TS = 19.51\)，对应的 \(p-\text{value}\) 为 0.0002。

因此，在 1% 的显著性水平下（实际上，在任何高于 0.02% 的显著性水平下），我们将拒绝这些国家中的不同女性在工作中受到虐待的比例相同这一假设。\(\blacksquare\)

11.6 用于连续数据的 Kolmogorov–Smirnov 拟合优度检验 \(^*\)

假设 \(Y_1,\ldots,Y_n\) 为来自连续分布的总体的样本数据，并且我们希望检验原假设 \(H_0: \text{总体的分布函数为} F\)，其中 \(F\) 是一个指定的连续分布函数。

一种检验 \(H_0\) 的方法是：

  • 首先将 \(Y_j\) 的可能取值划分为 \(k\) 个不同的区间，即 \((y_0,y_1),(y_1,y_2),\ldots,(y_{k - 1},y_k)\)，其中 \(y_0 = -\infty\)，\(y_k = +\infty\)。
  • 如果 \(Y_j\) 落在区间 \((y_{i - 1},y_i)\) 中，则令 \(Y_j^d = i\)。于是我们得到一个离散随机变量 \(Y_j^{d}\)，\(j = 1,\ldots,n\)。

原假设意味着 \(P\{Y_j^{d} = i\} = F(y_i)-F(y_{i - 1})\)，\(i = 1,\ldots,k\)，并且可以通过已经介绍过的卡方拟合优度检验来检验原假设。

然而，还有另一种比如上的离散化方法更为有效的检验方法以检验 \(Y_j\) 是否来自连续分布函数 \(F\)。接下来，我们将介绍这种更为有效的检验方法。

在观察到 \(Y_1,\ldots,Y_n\) 之后，令 \(F_e\) 为 经验分布函数（the empirical distribution function）：

\(F_e(x)=\frac{\#i:Y_i\leq x}{n}\)

也就是说，\(F_e(x)\) 是观察值中小于或等于 \(x\) 的比例。因为 \(F_e(x)\) 是一个观察值小于或等于 \(x\) 的概率的自然估计量，所以如果原假设（\(F\) 就是总体的分布函数）是正确的，那么 \(F_e(x)\) 和 \(F(x)\) 应该非常接近。由于对于所有的 \(x\) 都是如此，所以检验 \(H_0\) 的检验统计量为：

\(D\equiv\underset{x}{\text{Maximum}}|F_e(x)-F(x)|\)

其中在 \(x \in (-\infty, +\infty)\) 上取 \(|F_e(x)-F(x)|\) 的最大值作为统计量 \(D\)。我们称 \(D\) 为 Kolmogorov–Smirnov 检验统计量。

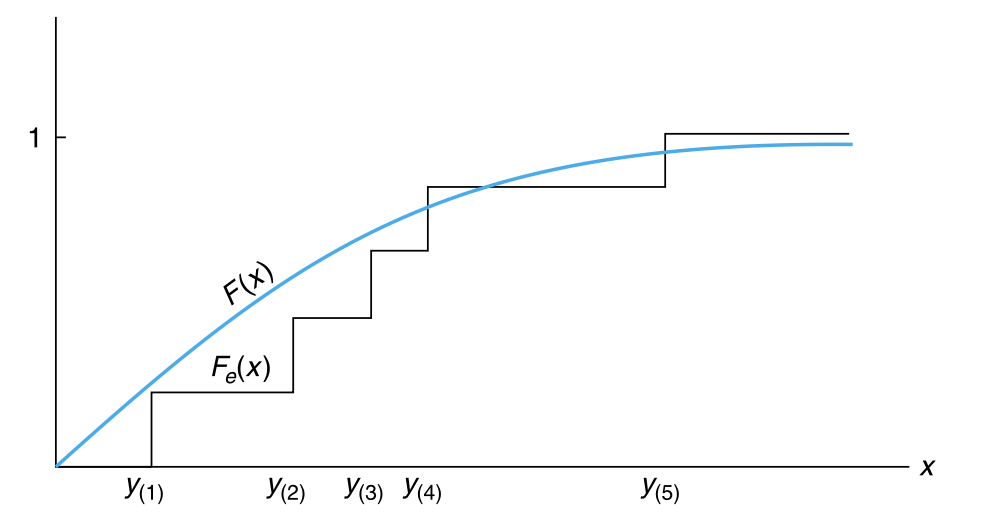
为了计算给定数据集 \(Y_j = y_j\)，\(j = 1,\ldots,n\) 下的 \(D\) 的值，我们令 \(y_{(1)},y_{(2)},\ldots,y_{(n)}\) 表示 \(y_j\) 的升序排列结果。也就是说，\(y_{(j)}\) 是 \(y_1,\ldots,y_n\) 中第 \(j\) 小的值。

例如，如果 \(n =3\)，\(y_1 = 3\)，\(y_2 = 5\)，\(y_3 = 1\)，那么 \(y_{(1)} = 1\)，\(y_{(2)} = 3\)，\(y_{(3)} = 5\)。所以，\(F_e(x)\) 可以写作：

\[ F_e(x) = \begin{cases} 0, \quad & \text{if} \quad x \lt y_{(1)} \\ \frac{1}{n}, \quad & \text{if} \quad y_{(1)} \le x \lt y_{(2)} \\ \vdots & \\ \frac{j}{n}, \quad & \text{if} \quad y_{(j)} \le x \lt y_{(j + 1)} \\ \vdots & \\ 1, \quad & \text{if} \quad y_{(n)} \le x \end{cases} \]

所以，在区间 \((y_{(j - 1)},y_{(j)})\) 内，\(F_e(x)\) 是常数，并在 \(y_{(1)},\ldots,y_{(n)}\) 处跃增 \(\frac{1}{n}\)。由于 \(F(x)\) 是 \(x\) 的增函数且小于等于 \(1\)，所以 \(F_e(x)-F(x)\) 的最大值是非负的，并且当 \(x\) 等于 \(y_{(j)}, j = 1,\ldots,n\) 中的一个时取得最大值（如 图 11.1）。

图 11.1: \(n=5\)

也就是说，

\[ \underset{x}{\text{Maximum}} \left \{ F_e(x)-F(x) \right \} =\underset{j = 1,\ldots,n}{\text{Maximum}}\{\frac{j}{n}-F(y_{(j)})\} \tag{11.4}\]

类似地，\(F(x)-F_e(x)\) 的最大值也是非负的，并且出现在紧靠跳跃点 \(y_{(j)}\) 的前一个的位置。所以：

\[ \underset{x}{\text{Maximum}}\{F(x)-F_e(x)\}=\underset{j = 1,\ldots,n}{\text{Maximum}}\{F(y_{(j)})-\frac{j - 1}{n}\} \tag{11.5}\]

根据 式 11.4 和 式 11.5，我们得到：

\[ \begin{align*} D&=\underset{x}{\text{Maximum}}\vert F_e(x)-F(x)\vert\\ &=\text{Maximum} \left \{\text{Maximum}\{F_e(x)-F(x)\},\text{Maximum}\{F(x)-F_e(x)\} \right \}\\ &=\text{Maximum} \left \{\frac{j}{n}-F(y_{(j)}),F(y_{(j)})-\frac{j - 1}{n},j = 1,\ldots,n \right \} \end{align*} \tag{11.6}\]

我们可以利用 式 11.6 来计算 \(D\) 的值。

假设已经观察到 \(Y_j\)，并且 \(Y_j\) 的观察值使得 \(D = d\)。较大的 \(D\) 值似乎与总体分布服从 \(F\) 的原假设不一致，所以观察数据集的 \(p-\text{value}\) 为：

\(p-\text{value}=P_F\{D\geq d\}\)

其中我们写作 \(P_F\) 是为了表明如上的概率是在原假设 \(H_0\) 为真（所以 \(F\) 就是总体的分布函数）的情况下计算的。

可以通过 命题 11.1 的模拟来更简单的近似计算如上的 \(p-\text{value}\)。命题 11.1 表明 \(P_F\{D\geq d\}\) 不依赖于总体的假设分布函数 \(F\)，这允许我们可以选择任何的连续分布 \(F\) 进行模拟来估计 \(p-\text{value}\)（因此，我们可以使用 \((0,1)\) 均匀分布）。

命题 11.1 对于任意的连续分布函数 \(F\)，\(P_F{D \ge d}\) 都是一样的。

证. \(\begin{align*} P_F\{D\geq d\}&=P_F\left\{\underset{x}{\text{Maximum}}\left|\frac{\#\{i:Y_i\leq x\}}{n}-F(x)\right|\geq d\right\}\\ &=P_F\left\{\underset{x}{\text{Maximum}}\left|\frac{\#\{i:F(Y_i)\leq F(x)\}}{n}-F(x)\right|\geq d\right\}\\ &=P\left\{\underset{x}{\text{Maximum}}\left|\frac{\#\{i:U_i\leq F(x)\}}{n}-F(x)\right|\geq d\right\} \end{align*}\)

其中，\(U_1,\ldots,U_n\) 是独立的 \((0,1)\) 均匀分布随机变量。

  • 第一个等式成立是因为 \(F\) 是增函数，所以 \(Y\leq x\) 等价于 \(F(Y)\leq F(x)\)
  • 第二个等式成立是因为如果 \(Y\) 具有连续分布函数 \(F\)，那么随机变量 \(F(Y)\) 为 \((0,1)\) 均匀分布（证明过程留作习题）。

令 \(y = F(x)\)，并且当 \(x\) 从 \(-\infty\) 增加到 \(+\infty\) 时，\(F(x)\) 从 \(0\) 增加到 \(1\) ，于是我们得到：

\(P_F\{D\geq d\}=P\left\{\underset{0\leq y\leq1}{\text{Maximum}}\left|\frac{\#\{i:U_i\leq y\}}{n}-y\right|\geq d\right\}\)

这表明，当原假设 \(H_0\) 为真时，\(D\) 的分布不依赖于实际分布 \(F\)。\(\blacksquare\)

由 命题 11.1 可知，在根据观察数据确定 \(D\) 的值（\(D = d\)）之后，可以使用 \((0,1)\) 均匀分布进行模拟来获得 \(p-\text{value}\)。也就是说，我们生成一个包含 \(n\) 个随机数 \(U_1,\ldots,U_n\) 的集合，然后检查 \(\underset{0\leq y\leq1}{\text{Maximum}}\left|\frac{\#\{i:U_i\leq y\}}{n}-y\right|\geq d\) 是否成立。重复这个过程很多次，那么 \(\underset{0\leq y\leq1}{\text{Maximum}}\left|\frac{\#\{i:U_i\leq y\}}{n}-y\right|\geq d\) 成立的次数比例就是对该数据集 \(p-\text{value}\) 的估计。如前所述，可以通过对随机数排序，然后使用等式

\(\text{Max}\left|\frac{\#\{i:U_i\leq y\}}{n}-y\right|=\text{Max}\left\{\frac{j}{n}-U_{(j)},U_{(j)}-\frac{j - 1}{n},j = 1,\ldots,n\right\}\)

来计算不等式的左边，其中 \(U_{(j)}\) 是 \(U_1,\ldots,U_n\) 中的第 \(j\) 小的值。

例如，如果 \(n = 3\) 且 \(U_1 = 0.7\)，\(U_2 = 0.6\)，\(U_3 = 0.4\)，那么 \(U_{(1)} = 0.4\)，\(U_{(2)} = 0.6\)，\(U_{(3)} = 0.7\)，这个数据集的 \(D\) 值为：

\(D=\text{Max}\left\{\frac{1}{3}-0.4,\frac{2}{3}-0.6,1 - 0.7,0.4,0.6-\frac{1}{3},0.7-\frac{2}{3}\right\}=0.4\) 。

令 \(D^{*}=(\sqrt{n}+0.12+\frac{0.11}{\sqrt{n}})D\)，并令 \(d_{\alpha}^{*}\) 满足 \(P_F\{D^{*}\geq d_{\alpha}^{*}\}=\alpha\)，则对于不同的 \(\alpha\) 值，\(d_{\alpha}^{*}\) 有以下的近似值：

\(d_{0.1}^{*}=1.224\)

\(d_{0.05}^{*}=1.358\)

\(d_{0.025}^{*}=1.480\)

\(d_{0.01}^{*}=1.626\)

如果 \(D^{*}\) 的观测值大于等于 \(d_{\alpha}^{*}\)，那么在显著性水平为 \(\alpha\) 下，我们将拒绝总体分布函数为 \(F\) 的原假设。

习题 11.8 假设我们要检验一个给定的总体分布是均值为 100 的指数分布的假设，即 \(F(x)=1-e^{-x/100}\)。如果来自该分布的、大小为 10 的样本的有序值为：

66、72、81、94、112、116、124、140、145、155

那么可以得出什么结论？

解 11.8. 首先，我们使用 式 11.6 来计算 Kolmogorov–Smirnov 检验统计量 \(D\) 的值。经过计算，我们得到 \(D = 0.4831487\)，所以：

\(D^{*}=0.48315(\sqrt{10}+0.12+\frac{0.11}{\sqrt{10}})=1.603\)。

因为 1.603 超过了 \(d_{0.025}^{*}=1.480\)，所以在 2.5% 的显著性水平下，我们将拒绝样本数据来自均值为 100 的指数分布的原假设。另一方面，因为 1.603 小于 \(d_{0.01}^{*}=1.626\)，所以在 1% 的显著性水平下，我们不会拒绝原假设。\(\blacksquare\)

Problems

  1. D. Phillips, “Death Day and Birthday: An Unexpected Connection,” in Statistics: A Guide to the Unknown, Holden-Day, 1972.↩︎