样本统计量的分布（Distributions of Sampling Statistics）也称为抽样分布，是指样本的统计指标的分布。例如，样本平均数是总体平均数的一个估计量，如果按照相同的样本容量，相同的抽样方式，反复地抽取样本，每次抽样可以得到一个平均数，所有可能样本的平均数所形成的分布，就是样本平均数的抽样分布。
统计学是一门从观测数据中得出结论的科学。例如，在技术研究中，经常遇到的一种情况是：我们可能会面对数量庞大的、具有可测量值（measurable values）的对象的集合。我们希望通过对这些数量庞大的对象适当抽样（sampling）并分析抽样得到的样本对象，从而得到一些和全部对象相关的结论。
为了使用样本数据（sample data）推断总体（pupulation），必须对样本与总体之间的关系作某些假设。通常，非常合理的一个假设是：总体会存在一个潜在的概率分布，因此可以认为，从总体中抽取的对象的测量值是独立随机变量并且其分布于总体分布一致。如果通过随机抽取的方式来获得样本数据，那么样本数据是独立、同总体分布一致这样的假设是合理的。
定义 6.1 如果 \(X_1, ..., X_n\) 是独立同分布的随机变量，其分布函数为 \(F\)，我们称 \(X_1, ..., X_n\) 构成了来自于 \(F\) 的 样本（sample）（有时也称其为随机样本）。
在大多数应用中，总体的分布 \(F\) 并非总是事先指定的（事实是，在大多数情况下，\(F\) 是未知的），因此我们会尝试使用数据来推断 \(F\)。
在使用样本数据推断总体分布的过程中，如果假定总体的潜在分布 \(F\) 是由一组未知参数确定的，则称其为 参数推断（parametric inference）；而如果对总体的潜在分布 \(F\) 没有任何假设，则称其为 非参数推断（nonparametric inference）。
例 6.1 假设刚刚安装了一个新工艺以用来生产计算机芯片，并且假设这个新工艺生产的连续芯片的使用寿命是独立、同分布的，其分布是一个未知分布 \(F\)。
物理原因有时会暗示分布 \(F\) 的参数形式。例如，物理原因可能会让我们相信 \(F\) 是一个正态分布或者是一个指数分布。在这种情况下，我们面对的将是一个 参数统计 问题，我们希望使用观察到的数据来估计 \(F\) 的参数。例如，如果假设 \(F\) 是正态分布，我们将希望估计其 均值 和 方差；如果假设 \(F\) 是指数分布，我们将希望估计其 均值。
在其他情况下，可能没有任何物理依据来假设 \(F\) 具有某种特定分布形式。在这种情况下，关于 \(F\) 的推断问题将构成一个 非参数推断 问题。
物理原因（Physical reasons）指的是基于物理学原理或物理现象的原因。在统计学和概率论中，物理原因通常涉及使用物理理论或实验结果来推导或假设某些统计分布的形式。例如，在某些情况下，物理现象可能会暗示数据遵循某种特定的分布：
在本章中，我们将关注由样本产生的某些统计量（或统计指标）的概率分布，其中 统计量（statistic）是一个随机变量，统计量的值由样本数据决定。我们将讨论的两个重要的统计量：样本均值 和 样本方差。
考虑一个总体，总体中的每个元素都有一个数字类型的值（value）。例如，总体可能由特定社区的成年人构成，总体中和每个成年人相关的数字类型的值可能是其年收入、身高或年龄等。我们经常假设，与总体中的任何成员相关的值都可以看作期望为 \(\mu\)、方差为 \(\sigma^2\) 的随机变量的取值。我们称 \(\mu\) 为总体均值，称 \(\sigma^2\) 为总体方差。令 \(X_1, X_2, ..., X_n\) 是从该总体中抽取的样本的值，则样本均值的定义为：
\[ \overline{X} = \frac{X_1 + ... + X_n}{n} \]
因为样本均值 \(\overline{X}\) 的值取决于样本中的各随机变量的值，因此 \(\overline{X}\) 也是一个随机变量。\(\overline{X}\) 的期望和方差分别为：
\[ \begin{align} E[\overline{X}] &= E\bigg[\frac{X_1 + ... + X_n}{n}\bigg] \\ &= \frac{1}{n}(E[X_1] + ... + E[X_n]) \\ &= \mu \\ \textup{Var}(\overline{X}) &= \textup{Var}\bigg(\frac{X_1 + ... + X_n}{n}\bigg) \\ &= \frac{1}{n^2}\bigg(\textup{Var}(X_1) + ... + \textup{Var}(X_n) \bigg) \\ &= \frac{n\sigma^2}{n^2} \\ &= \frac{\sigma^2}{n} \end{align} \tag{6.1}\]
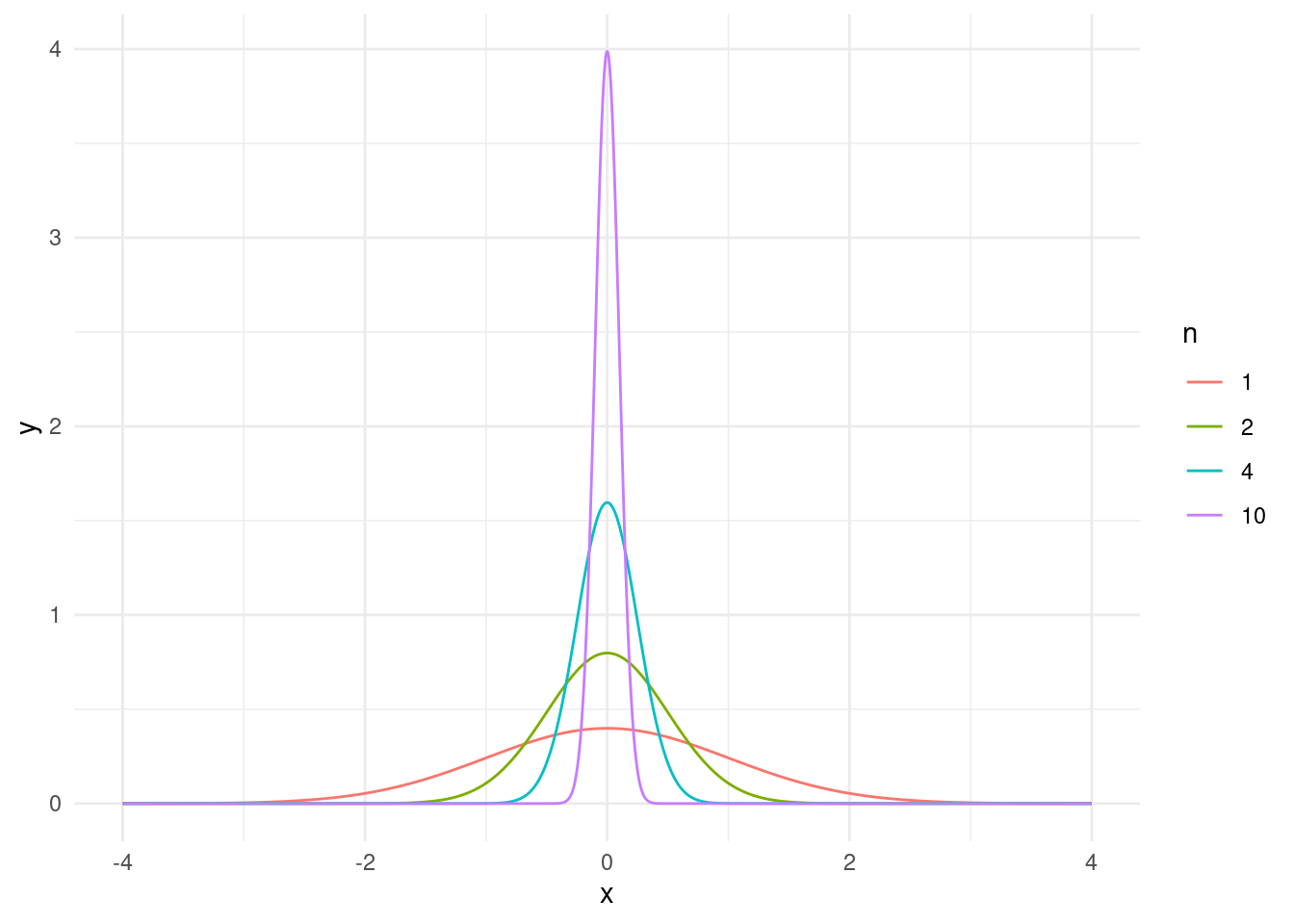
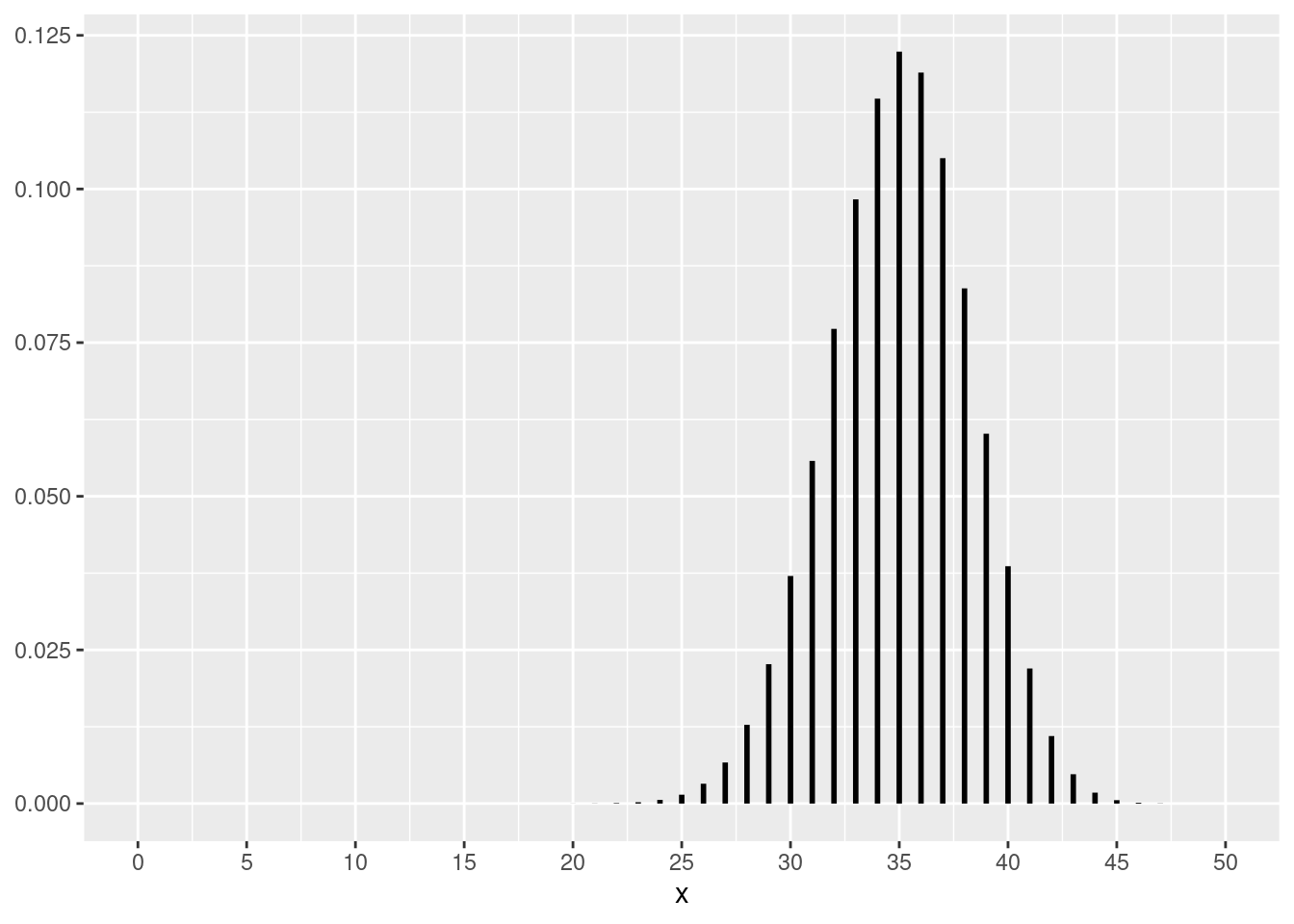
其中，\(\mu\) 和 \(\sigma^2\) 分别为总体的均值和方差。因此，样本均值的期望就是总体均值 \(\mu\)，而样本均值的方差就是总体方差的 \(\frac{1}{n}\) 倍。因此，我们可以得出结论：\(\overline{X}\) 也是以总体均值 \(\mu\) 为中心，但是其波动会随着样本量的增加而变得越来越小。图 6.1 绘制了来自标准正态分布总体的、不同样本量的样本均值的概率密度函数。
library(ggplot2)
distributions <- data.frame(
x = rep(seq(-4, 4, length = 1000), 4),
mean = rep(c(0, 0, 0, 0), each = 1000),
sd = rep(c(1, 0.5, 0.25, 0.1), each = 1000),
n = rep(c(1, 2, 4, 10), each = 1000)
)
# 计算每个分布的概率密度
distributions$y <- with(distributions, dnorm(x, mean=mean, sd=sd))
# 绘制多个正态分布的曲线
ggplot(distributions, aes(x=x, y=y, color=factor(n))) +
geom_line() +
labs(color="n") +
theme_minimal()
在本节中，我们将讨论概率论中最为显著的一个结果——即中心极限定理（the central limit theorem）。简单的说，中心极限定理断言：大量的、独立随机变量的和的分布近似于正态分布。因此，对于独立随机变量的和而言，中心极限定理不仅提供了一种计算其近似概率的简单方法，而且还有助于解释许多自然总体的经验频率呈现钟形曲线（即正态分布）的这一显著现象。
中心极限定理的最简单的形式如下：
定理 6.1 中心极限定理：令 \(X_1, X_2, ..., X_n\) 是一个独立、同分布的随机变量的序列，其中每个随机变量的均值和方差均为 \(\mu\) 和 \(\sigma^2\)。对于一个比较大的 \(n\)，
\(X_1 + X_2 + \cdots + X_n\)
的分布近似于均值为 \(n\mu\)、方差为 \(n\sigma^2\) 的正态分布。\(\blacksquare\)
根据 定理 6.1，\(\frac{X_1 + X_2 + \cdots + X_n - n\mu}{\sqrt{n}\sigma}\) 的分布近似于标准正态分布 \(\mathcal{N}(0,1)\)。因此，如果 \(Z \thicksim \mathcal{N}(0, 1)\)，对于一个比较大的 \(n\)，有：
\[ P\bigg\{\frac{X_1 + X_2 + \cdots + X_n - n\mu}{\sqrt{n}\sigma} \lt x \bigg\} \approx P\{Z \lt x\} \]
习题 6.1 一家保险公司有 25000 名汽车保险的投保人。如果投保人的年度索赔额是均值为 320、标准差为 540 的随机变量，则投保人年度索赔总额超过 830 万元的概率是多少？
解 6.1. 令 \(X\) 表示年度索赔总额。对投保人进行编号，令 \(X_i\) 表示第 \(i\) 位投保人的年度索赔额。当 \(n = 25000\) 时，根据中心极限定理，\(X = \sum_{i=1}^{n}{X_i}\) 将近似于均值为 \(320 \times 25000 = 8 \times 10^6\)、标准差为 \(540 \sqrt{25000} = 8.5381 \times 10^4\) 的正态分布。因此：
\[ \begin{align} P\{X > 8.3 \times 10^6\} &= P\bigg\{\frac{X - 8 \times 10^6}{8.5381 \times 10^4} \gt \frac{8.3 \times 10^6 - 8 \times 10^6}{8.5381 \times 10^4} \bigg\} \\ &= P\bigg\{\frac{X - 8 \times 10^6}{8.5381 \times 10^4} \gt \frac{0.3 \times 10^6}{8.5381 \times 10^4} \bigg\} \\ & \approx P\{Z \gt 3.51 \} \\ & \approx 0.00023 \end{align} \]
因此，年索赔额超过 830 万元的概率仅仅只有万分之 2.2。当然我们也可以使用 R 来计算待求的概率：
1 - pnorm(8.3 * 10^6, 320 * 25000, 540 * sqrt(25000))1 - pnorm(8.3 * 10^6, 320 * 25000, 540 * sqrt(25000))[1] 0.0002210042\(\blacksquare\)
习题 6.2 土木工程师认为：在没有结构性损坏的情况下，某跨度的桥所能承受的重量（单位为 1000 磅）\(W\) 是一个均值为 400、标准差为 40 的正态分布。假设一辆汽车的重量（同样以 1000 磅为单位）是一个均值为 3、标准差为 0.3 的随机变量。该桥上必须有多少辆汽车才能使其发生结构性损坏的概率超过 0.1？
解 6.2. 令 \(P_n\) 表示当桥上有 \(n\) 辆车时桥发生结构性损坏的概率。令 \(X_i\) 表示桥上第 \(i\) 辆汽车的重量，于是有：
\(\begin{align} P_n &= P\{X_1 + \cdots + X_n \ge W\} \\ &= P\{X_1 + \cdots + X_n - W \ge 0\} \end{align}\)
根据中心极限定理（定理 6.1），\(\sum_{i=1}^{n}{X_i}\) 近似于均值为 \(3n\)、方差为 \(0.09n\) 的正态分布。因为 \(W\) 是与 \(X_i\) 之间相互独立的正态分布，因此 \((\sum_{i=1}^{n}{X_i}) - W\) 也是一个正态分布，并且其均值和方差分别为：
\(E\bigg[(\sum_{i=1}^{n}{X_i}) - W\bigg] = 3n - 400\)
\(\textup{Var}\bigg((\sum_{i=1}^{n}{X_i}) - W\bigg) = \textup{Var}\bigg(\sum_{i=1}^{n}{X_i}\bigg) + \textup{Var}(W) = 0.09n + 1600\)
令 \(Z\) 表示标准正态分布的随机变量，所以有：
\(\begin{align} P_n &= P\bigg\{\frac{X_1 + \cdots + X_n - W - (3n - 400)}{\sqrt{0.09n + 1600}} \ge \frac{0 - (3n - 400)}{\sqrt{0.09n + 1600}}\bigg\} \\ & \approx P\bigg\{Z \ge \frac{400 - 3n}{\sqrt{0.09n + 1600}} \bigg\} \end{align}\)
在 R 语言中，利用 qnorm(0.1, lower.tail = FALSE) 求解 \(P\{X \gt x\}\) 的概率可得到 \(P\{Z \ge 1.28\} \approx 0.1\)。
qnorm(0.1, lower.tail = FALSE)[1] 1.281552所以当汽车数量满足 \(\frac{400 - 3n}{\sqrt{0.09n + 1600}} \le 1.28\) 时，即 \(n \ge 117\) 时，桥会有 10% 的概率发生结构性损坏。\(\blacksquare\)
对二项随机变量的研究是中心极限定理最重要的应用之一。由于二项随机变量 \(X\) 以参数 \((n, p)\) 表示在试验成功概率为 \(p\) 时 \(n\) 个独立试验的成功次数。如果令
\(X_i = \begin{cases} 1, \quad & 第 i 次试验成功\\ 0, \quad & 其它 \end{cases}\)
则我们可以将 \(X\) 表示为：
\(X = X_1 + \cdots + X_n\)
因为 \(E[X_i] = p\)，\(\textup{Var}(X_i) = np(1-p)\)，所以根据中心极限定理，当 \(n\) 比较大时：
\(\frac{X - np}{\sqrt{np(1-p)}}\) 近似于标准正态分布。
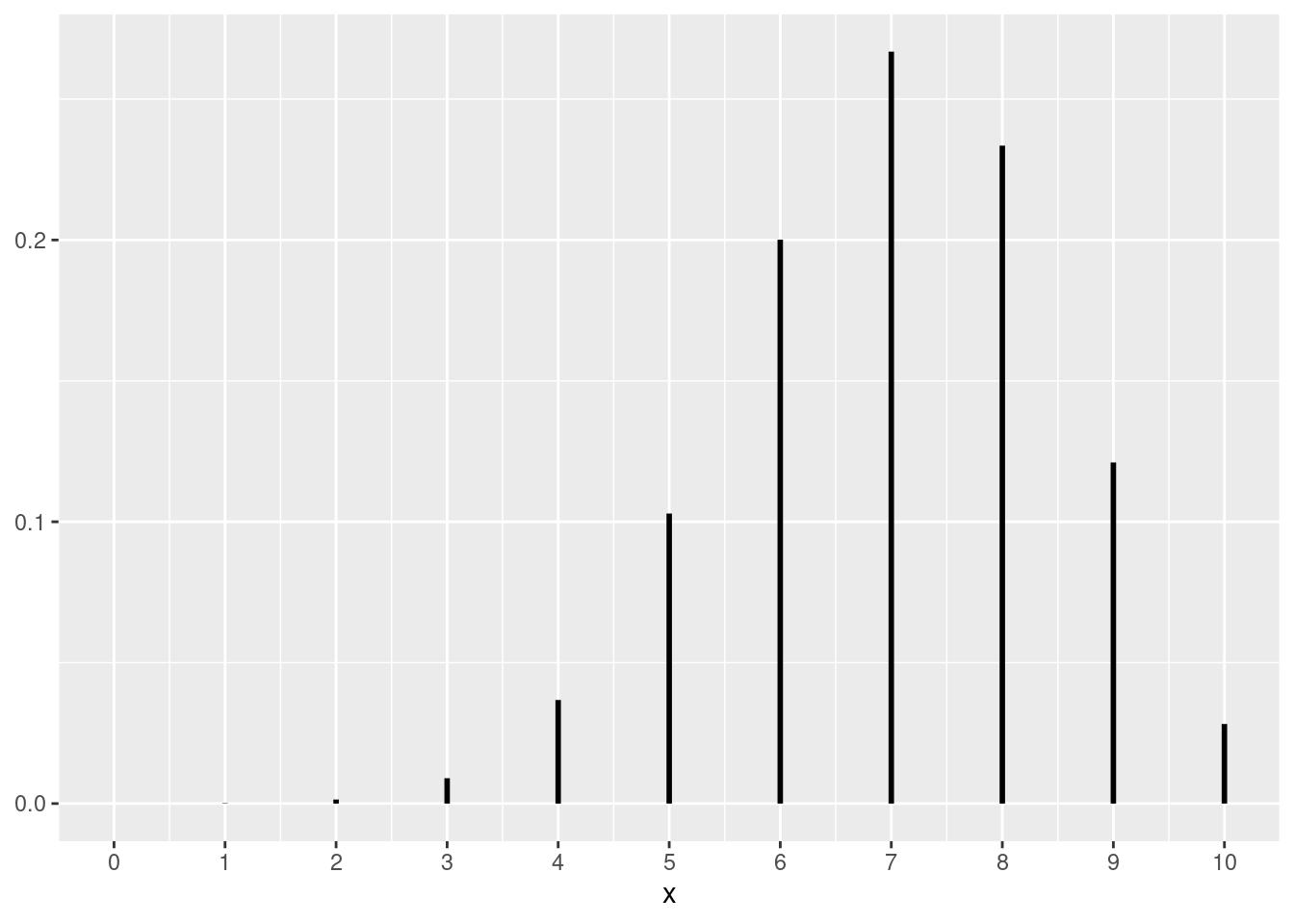
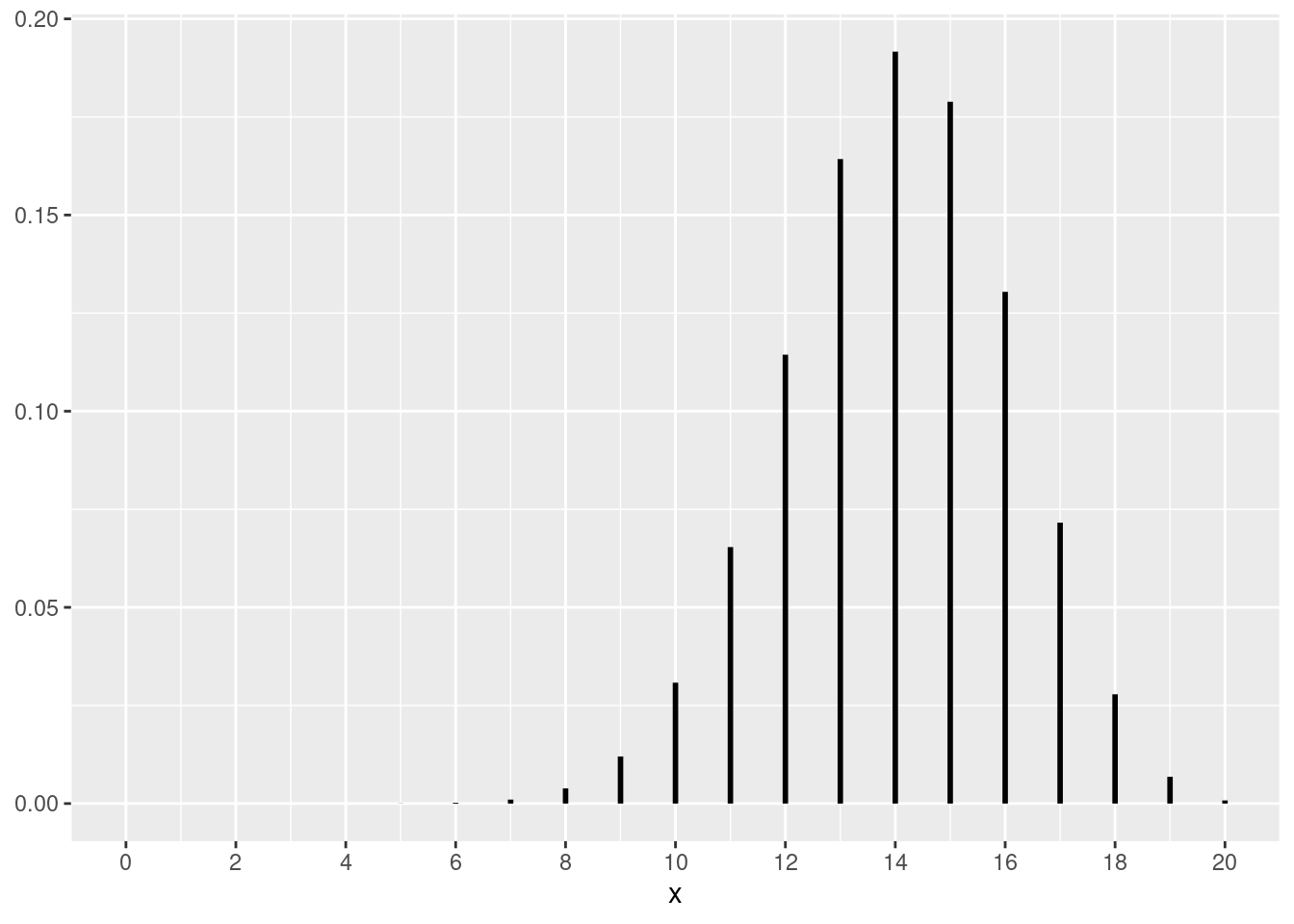
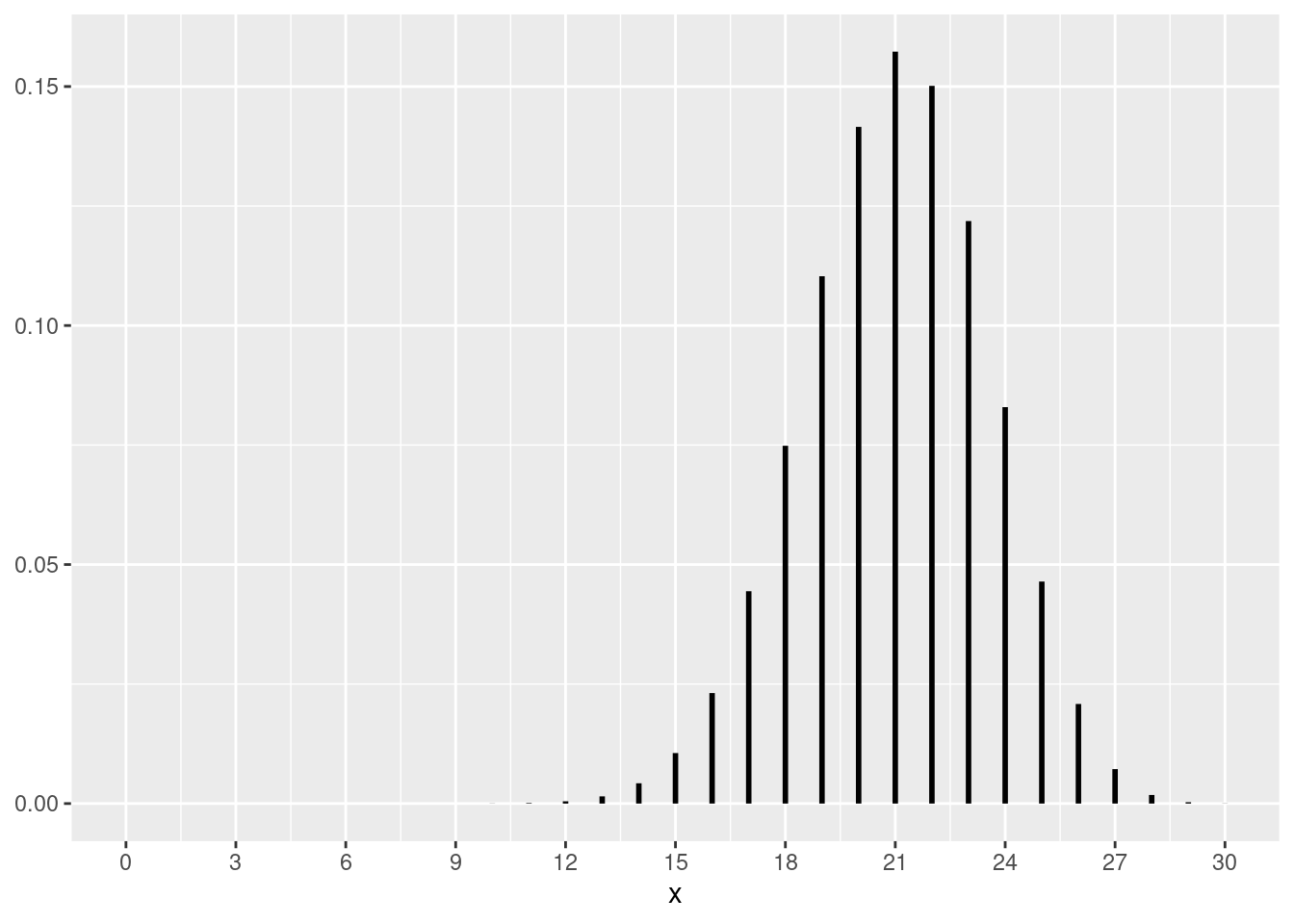
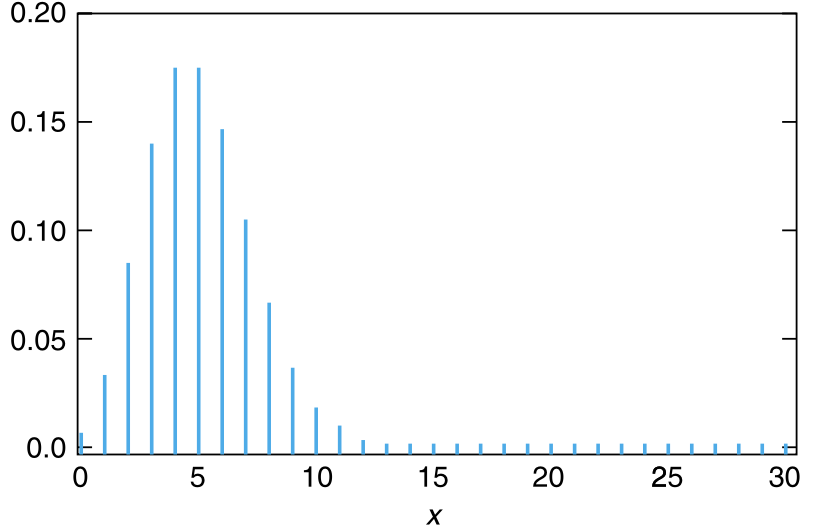
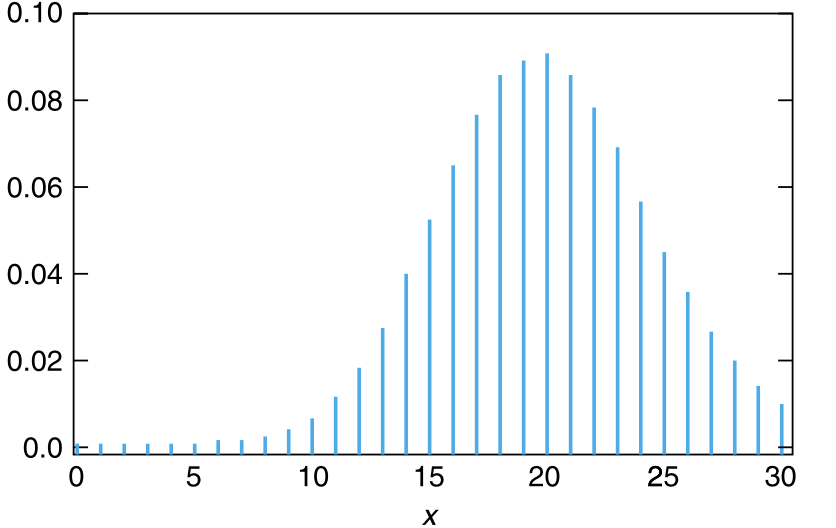
图 6.2 以图形的方式给出了参数为 \((n,p)\) 的二项随机变量的概率质量函数是如何随着 \(n\) 的增大而变得越来越趋向于正态分布。
library(ggplot2)
n_seq = c(10, 20, 30, 50)
p <- 0.7
i <- 1
g_list <- list()
for (n in n_seq) {
x <- seq(0, n, 1)
y <- dbinom(x, n, p)
df <- data.frame(x = x, y = y, y_start = rep(0, n + 1))
plot <- ggplot(df, aes(x = x, y = y_start, yend = y)) +
geom_segment(size = 1) +
scale_x_continuous(breaks = seq(0, n, n / 10), limits = c(0, n)) +
#labs(title = paste("(", n, ",", p, ")")) +
theme(axis.title.y = element_blank())
g_list[[i]] <- plot
i <- i + 1
}
for (g in g_list) {
print(g)
}
习题 6.3 某所大学的一年级学生的理想人数是 150。根据过去的经验，平均而言，收到录取通知书的学生中，只有 30% 会真正入学，因此该学校采用发放 450 份录取通知书的政策。计算该学校的一年级学生人数超过 150 的概率？
解 6.3. 令 \(X\) 表示入学的学生数量，假定每个收到入学通知书的学生最终是否入学是相互独立的，因此 \(X\) 是一个参数为 \((450, 0.3)\) 的二项随机变量。因为二项分布是离散分布，而正态分布是连续分布，因此当使用正态分布来近似计算时，最好使用 \(P\{i - 0.5 < X < i + 0.5\}\) 来计算 \(P\{X=i\}\)（也称为连续性校正（Continuity Correction））。令 \(Z \thicksim \mathcal{N}(0,1)\)，则近似概率为：
\(\begin{align} P\{X \gt 150.5\} &= P\bigg\{\frac{X - 450 \cdot 0.3}{\sqrt{450 \cdot 0.3 \cdot 0.7}} \gt \frac{150.5 - 450 \cdot 0.3}{\sqrt{450 \cdot 0.3 \cdot 0.7}} \bigg\} \\ & \approx P\{Z \gt 1.59\} \\ & \approx 0.06 \end{align}\)
pnorm(1.59, lower.tail = FALSE)pnorm(1.59, lower.tail = FALSE)[1] 0.0559174因此，在收到录取通知书的 450 名学生中，实际入学超过 150 名学生的概率只有 6%。\(\blacksquare\)
连续性校正（Continuity Correction），有时也称为 Yates 连续性校正，是统计学中用于修正离散分布（如二项分布）和连续分布（如正态分布）之间差异的一种方法。具体来说，当我们使用连续的正态分布来近似离散的二项分布时，连续性校正可以提高近似的精确度。
需要注意的是，对于二项分布，我们现在有两种可能的近似方式：
令 \(X_1, ..., X_n\) 是从均值为 \(\mu\)、方差为 \(\sigma^2\) 的总体中抽取的样本。可以使用中心极限定理来近似样本均值 \(\overline{X}\) 的分布：
\(\overline{X} = \sum_{i=1}^{n}{\frac{X_i}{n}}\)
根据中心极限定理，当 \(n\) 比较大时，\(\overline{X}\) 近似于正态分布。根据 式 6.1，\(\overline{X}\) 的期望和标准差分别为 \(\mu\) 和 \(\frac{\sigma}{\sqrt{n}}\)，因此：
\[ \frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \]
近似于标准正态分布。
习题 6.4 一个工人总体的体重的均值为 167，标准差为 27。
解 6.4. 令 \(Z \thicksim \mathcal{N}(0,1)\)。
根据中心极限定理，\(\overline{X}\) 近似服从均值为 167、标准差为 \(\frac{27}{\sqrt{36}} = 4.5\) 的正态分布。因此：
\(\begin{align} P\{163 \lt \overline{X} \lt 170\} &= P\bigg\{\frac{163 - 167}{4.5} \lt \frac{\overline{X} - 167}{4.5} \lt \frac{170 - 167}{4.5} \bigg\} \\ & \approx P\{-0.8889 \lt Z \lt 0.8889\} \\ &= P\{Z \lt 0.8889\} - P\{Z \lt -0.8889\} \\ &= 1 - 2 \cdot P\{Z \ge 0.8889\} \\ &= 0.6259432 \end{align}\)
可以用如下 R 代码 1 - 2 * pnorm(0.8889, lower.tail = FALSE) 求解 \(1 - 2 \cdot P\{Z \ge 0.8889\}\) 的值：
1 - 2 * pnorm(0.8889, lower.tail = FALSE)[1] 0.6259432当样本量为 144 时，近似服从均值为 167、标准差为 \(\frac{27}{\sqrt{144}} = 2.25\) 的正态分布。因此：
\(\begin{align} P\{163 \lt \overline{X} \lt 170\} &= P\bigg\{\frac{163 - 167}{2.25} \lt \frac{\overline{X} - 167}{2.25} \lt \frac{170 - 167}{2.25} \bigg\} \\ & \approx P\{-1.7778 \lt Z \lt 1.7778\} \\ &= P\{Z \lt 1.7778\} - P\{Z \lt -1.7778\} \\ &= 1 - 2 \cdot P\{Z \ge 1.7778\} \\ &= 0.9245633 \end{align}\)
因此，当样本大小从 36 增加到 144 时，工人体重的样本均值在 163~170 之间的近似概率从 0.6259 提升到了 0.9246。\(\blacksquare\)
习题 6.5 一位天文学家想测量从她的观测台到一颗遥远恒星的距离。然而，由于大气扰动的原因，任何测量都不会产生确切的距离 \(d\)。因此，天文学家决定进行一系列测量，然后使用它们的平均值作为实际距离的估计。如果天文学家认为连续测量的距离之间是独立的随机变量，其均值为 \(d\) 光年，标准差为 2 光年，则天文学家需要做多少次测量才能使得她所估计的距离误差在 \(\pm 0.5\) 光年之内的概率至少为 95%？
解 6.5. 如果天文学家测量了 \(n\) 次，则测量数据的样本均值 \(\overline{X}\) 将近似服从均值为 \(d\)、标准差为 \(\frac{2}{\sqrt{n}}\) 的正态分布。因此，测量值位于 \(d \pm 0.5\) 之间的概率为：
\(\begin{align} P\{-0.5 \lt \overline{X} - d \lt 0.5\} &= P\bigg\{\frac{-0.5}{\frac{2}{\sqrt{n}}} \lt \frac{\overline{X} - d}{\frac{2}{\sqrt{n}}} \lt \frac{0.5}{\frac{2}{\sqrt{n}}} \bigg\} \\ & \approx P\{-\frac{\sqrt{n}}{4} \lt Z \lt \frac{\sqrt{n}}{4}\} \\ &= 1 - 2 \cdot P\{Z \ge \frac{\sqrt{n}}{4}\} \end{align}\)
即，\(1 - 2 \cdot P\{Z \ge \frac{\sqrt{n}}{4}\} \ge 0.95\)，也就是 \(P\{Z \ge \frac{\sqrt{n}}{4}\} \le 0.025\)。
在 R 中，利用 qnorm(0.025, lower.tail = FALSE) 可以得到 \(Z\) 的最小值 1.959964，即 \(\frac{\sqrt{n}}{4} \ge 1.959964\)。
qnorm(0.025, lower.tail = FALSE)[1] 1.959964于是得到 \(n \ge 61.46334\)，因此，天文学家至少要测量 62 次。\(\blacksquare\)
中心极限定理并没有明确指出：样本大小 \(n\) 需要多大才能使逼近的正态分布是有效的。事实上，答案取决于样本数据的总体分布。
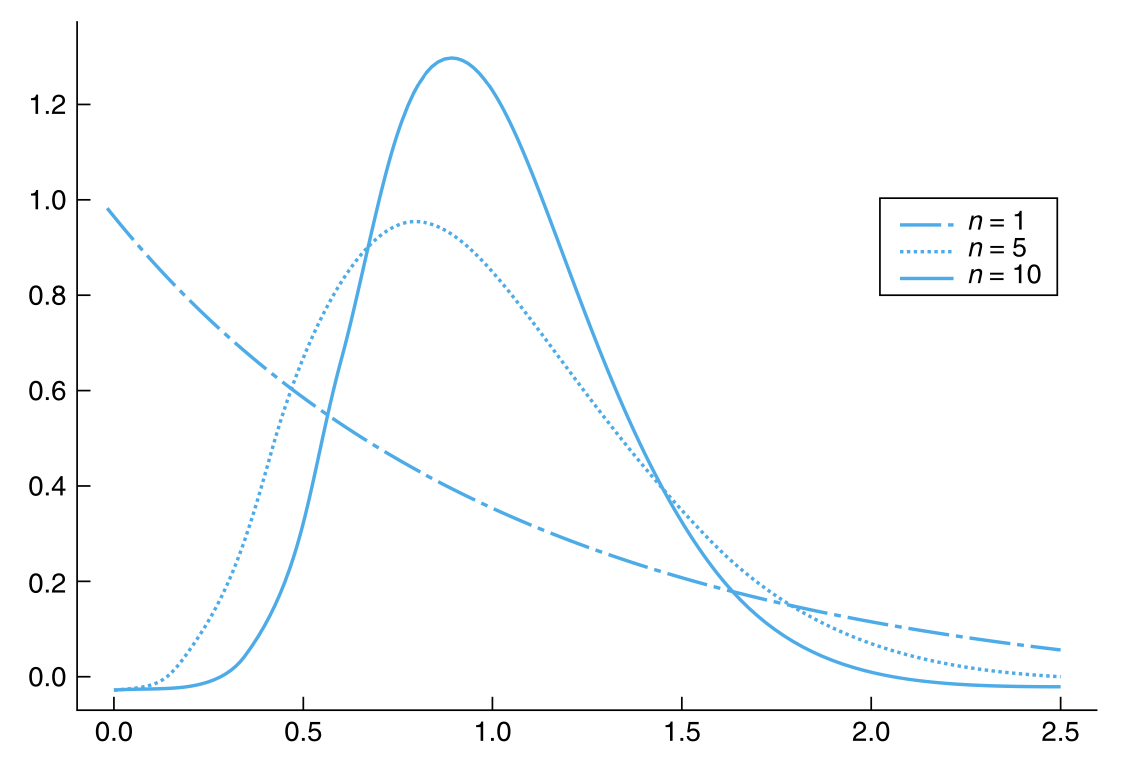
例如，如果总体潜在的分布是正态分布，那么无论样本量大小是多少，样本均值 \(\overline{X}\) 也都将是正态分布。一般的经验是：只要样本量 \(n\) 至少为30，就可以确信 \(\overline{X}\) 近似服从正态分布。也就是说，实际上，无论总体的潜在分布有多不服从正态分布，至少有 30 个样本的样本均值都将近似服从正态分布。在大多数情况下，正态逼近也适用于样本量小得多的场景。事实上，大小为 5 的样本通常就足以让正态逼近是有效的。当总体分布为指数分布时，图 6.3 显示了样本大小 \(n\) 分别为 1、5、10 时的样本均值的分布。
令 \(X_1, ..., X_n\) 是从均值为 \(\mu\)、方差为 \(\sigma^2\) 的总体中抽取的随机样本。令 \(\overline{X}\) 为样本均值，然后回顾一下 小节 2.3.2 节中的 定义 2.3。
定义 6.2 令 \(S^2\) 为样本方差，则样本方差的定义如下：
\[ S^2 = \frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{n-1} \]
\(S = \sqrt{S^2}\) 为样本标准差。
为了计算 \(E[S^2]\)，我们需要用到在 小节 2.3.2 中已经证明过的 式 2.5，即：对于任意的 \(x_1, ..., x_n\)，
\(\sum_{i=1}^{n}{(x_i - \overline{x})^2} = \sum_{i=1}^{n}{x_i^2} - n\overline{x}^2\)，其中 \(\overline{x} = \frac{\sum_{i=1}^{n}{x_i}}{n}\)。
\[ (n-1)S^2 = \sum_{i=1}^{n}{X_i^2} - n\overline{X}^2 \tag{6.2}\]
根据 式 4.47，对于任意的随机变量 \(X\)，\(E[X^2] = \textup{Var}(X) + (E[X])^2\)。对 式 6.2 两边求期望得到：
\[ \begin{align} (n-1)E[S^2] &= E\bigg[\sum_{i=1}^{n}{X_i^2}\bigg] - nE[\overline{X}^2] \\ &= nE[X_1^2] - nE[\overline{X}^2] \\ &= n \textup{Var}(X_1) + n(E[X_1])^2 - n \textup{Var}(\overline{X}) - n (E[\overline{X}])^2 \\ &= n \sigma^2 + n \mu^2 - n \frac{\sigma^2}{n} - n \mu^2 \\ &= (n-1)\sigma^2 \\ \therefore E[S^2] &= \sigma^2 \end{align} \]
也就是说，样本方差 \(S^2\) 的期望等于总体的方差 \(\sigma^2\)。
令 \(X_1, X_2, ..., X_n\) 是从均值为 \(\mu\)、方差为 \(\sigma^2\) 的正态分布总体中抽取的样本。也就是说，\(X_i\) 之间是独立且同分布的，并且 \(X_i \thicksim \mathcal{N}(\mu, \sigma^2)\)。
同时，令 \(\overline{X} = \frac{\sum_{i=1}^{n}{X_i}}{n}\) 表示样本均值，令 \(S^2 = \frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{n-1}\) 表示样本方差。接下来，我们就将计算 \(\overline{X}\) 和 \(S^2\) 的分布。
因为独立的、正态分布的随机变量的和也是正态分布，因此，\(\overline{X}\) 也是正态分布，其均值和方差分别为：
\(E[\overline{X}] = \sum_{i=1}^{n}{\frac{E[X_i]}{n}} = \mu\)
\(\textup{Var}(\overline{X}) = \frac{1}{n^2}\sum_{i=1}^{n}{\textup{Var}(X_i)} = \frac{\sigma^2}{n}\)
也就是说，随机样本的平均值 \(\overline{X}\) 是一个均值为总体均值、但是方差为总体方差 \(\frac{1}{n}\) 倍的正态分布。因此，
\(\frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}}\) 是一个标准正态分布。
在本节中，我们不仅会计算样本方差 \(S^2\) 的分布，还发现了关于正态分布随机样本的一个基本事实：即 \(\overline{X}\) 和 \(S^2\) 是相互独立的随机变量，并且 \(\frac{(n-1)S^2}{\sigma^2}\) 服从自由度为 \(n−1\) 的卡方（chi-square）分布。
对于 \(x_1, ..., x_n\)，令 \(y_i = x_i - \mu\)，则 \(\overline{y} = \overline{x} - \mu\)，根据：
\[ \sum_{i=1}^{n}{(y_i - \overline{y})^2} = \sum_{i=1}^{n}{y_i^2} - n\overline{y}^2 \]
有：
\[ \sum_{i=1}^{n}{(x_i - \overline{x})^2} = \sum_{i=1}^{n}{(x_i - \mu)^2} - n(\overline{x} - \mu)^2 \tag{6.3}\]
如果 \(X_1, ..., X_n\) 是从均值为 \(\mu\)、方差为 \(\sigma^2\) 的正态分布总体中抽取的样本，根据 式 6.3 有：
\[ \frac{\sum_{i=1}^{n}{(X_i - \mu)^2}}{\sigma^2} = \frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{\sigma^2} + \frac{n(\overline{X} - \mu)^2}{\sigma^2} \]
即，
\[ \sum_{i=1}^{n}{\bigg(\frac{X_i - \mu}{\sigma}\bigg)^2} = \frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{\sigma^2} + \bigg(\frac{\sqrt{n}(\overline{X} - \mu)}{\sigma}\bigg)^2 \tag{6.4}\]
因为 \(\frac{X_i - \mu}{\sigma}\) 是相互独立的标准正态分布，所以 式 6.4 中的等式左边是一个自由度为 \(n\) 的卡方随机变量。又根据 小节 6.5.1 可知，\(\frac{\sqrt{n}(\overline{X} - \mu)}{\sigma}\) 也是一个标准正态分布，因此，\(\bigg(\frac{\sqrt{n}(\overline{X} - \mu)}{\sigma}\bigg)^2\) 是一个自由度为 1 的卡方随机变量。因此 式 6.4 等价于一个自由度为 \(n\) 的卡方随机变量 是两个随机变量的和，其中一个随机变量是自由度为 1 的卡方随机变量。同时已知两个独立卡方随机变量之和也是卡方随机变量，并且其自由度为这两个独立的卡方随机变量的自由度之和。因此，看起来，式 6.4 右边的两部分是相互独立的、并且 \(\frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{\sigma^2}\) 服从自由度为 \(n-1\) 的卡方分布。结果确实如此，因此我们有以下基本结论。
定理 6.2 如果 \(X_1, ..., X_n\) 是从均值为 \(\mu\)、方差为 \(\sigma^2\) 的正态分布总体中抽取的样本，则
对于一个正态分布的总体而言，定理 6.2 不但给出了 样本均值 \(\overline{X}\) 和样本方差 \(S^2\) 的分布，而且还给出了 \(\overline{X}\) 和 \(S^2\) 之间是相互独立的这一重要事实。事实上，\(\overline{X}\) 和 \(S^2\) 的这种独立性是正态分布的一个特性。定理 6.2 的重要性将在后续的章节中得以明显的体现。
习题 6.6 CPU 处理某类作业（job）所需的时间服从均值为 20 秒、标准差为 3 秒的正态分布。如果观察到 15 个这样的作业，则样本方差超过 12 的概率是多少？
解 6.6. 因为样本的大小 \(n = 15\)，样本方差 \(\sigma^2 = 9\)，因此：
\(P\{S^2 > 12\} = P\bigg\{\frac{14}{9} S^2 \gt \frac{14}{9} \cdot 12\bigg\}\)
在 R 中利用 1 - pchisq(56/3, 14) 进行计算得到：
1 - pchisq(56/3, 14)[1] 0.1780811\(\blacksquare\)
在后续章节中，定理 6.2 的如下推论将非常有用。
推论 6.1 如果 \(X_1, ..., X_n\) 是从均值为 \(\mu\) 的正态分布总体中抽取的样本。如果 \(\overline{X}\) 为样本均值，\(S\) 为样本标准差，则：
\[ \sqrt{n} \frac{\overline{X} - \mu}{S} \thicksim t_{n-1} \]
也就是说，\(\sqrt{n} \frac{\overline{X} - \mu}{S}\) 服从自由度为 \(n-1\) 的 \(t\) 分布。
证. 回想一下，自由度为 \(n\) 的 \(t\) 分布随机变量的定义为：
\(\frac{Z}{\sqrt{\frac{\chi_n^2}{n}}}\)
其中，\(Z\) 为标准正态分布随机变量，并且与自由度为 \(n\) 的卡方随机变量 \(\chi_n^2\) 相互独立。根据 定理 6.2，\(\frac{\sqrt{n}(\overline{X} - \mu)}{\sigma}\) 是一个标准正态分布并且与自由度为 \(n-1\) 的卡方分布随机变量 \(\frac{(n-1)S^2}{\sigma^2}\) 相互独立。因此，我们有：
\(\frac{\sqrt{n}(\overline{X} - \mu) / \sigma}{\sqrt{S^2 / \sigma^2}} = \sqrt{n} \frac{(\overline{X} - \mu)}{S}\)
是一个自由度为 \(n-1\) 的 \(t\) 分布随机变量。\(\blacksquare\)
考虑一个包含 \(N\) 个元素的总体，假设该总体中具有某种特征的个体占比是 \(p\)，也就是说有 \(Np\) 个个体具备该特征，而 \(N(1-p)\) 个个体不具备该特征。从该总体中抽取大小为 \(n\) 的样本，如果对于 \(\left(\begin{array}{cc} N \\ n \end{array}\right)\) 种抽取方式中的每一种都是等概率抽取的，则我们称抽取到的样本为 随机样本（random sample）。例如，如果总体由 \(a\)、\(b\)、\(c\) 三个元素构成，则选择大小为 2 的随机样本，以便\(\{a,b\}\)、\(\{a,c\}\) 和 \(\{b,c\}\) 都有同样的可能性成为样本。可以通过以下方式可以依次选择一个随机样本：让随机样本的第一个元素等可能地为总体的 \(N\) 个元素中的任何一个，然后让其第二个元素等可能地为总体的剩余 \(N - 1\) 个元素中的任何一个，依此类推。
假设从大小为 \(N\) 的总体中抽取大小为 \(n\) 的随机样本。对于 \(i = 1, ..., n\)，令
\(X_i = \begin{cases} 1, \quad & 第 i 个元素具备某种特征\\ 0, \quad & 其它 \end{cases}\)
现在我们考虑 \(X_i\) 的和，也就是：
\(X = X_1 + X_2 + \cdots + X_n\)
如果样本的第 \(i\) 个成员具有该特征，则 \(X_i\) 对总和的贡献为 1，否则贡献为 0，因此 \(X\) 等于样本中具有该特征的成员的数量。
此外，样本均值
\(\overline{X} = \frac{X}{n} = \sum_{i=1}^{n}{\frac{X_i}{n}}\)
等于样本中具备该特征的成员的占比。
现在让我们考虑 \(X\) 和 \(\overline{X}\) 的统计量的概率分布。首先，请注意，由于总体中 \(N\) 个成员中的每一个都有相同的可能是样本的第 \(i\) 个成员，因此：
\(P\{X_i = 1\} = \frac{Np}{N} = p\)
同理，
\(P\{X_i = 0\} = 1 - P\{X_i = 1\} = 1 - p\)
也就是说，每一个 \(X_i\) 为 1 的概率都是 \(p\)，为 0 的概率都是 \(1 - p\)。
需要特别注意的是：随机变量 \(X_1, X_2, ..., X_n\) 并不是相互独立的。例如，由于第二次所选择的成员可以是总体 \(N\) 个成员中的任何一个，因此第二次选择的成员具有该特征的概率是 \(\frac{Np}{N}=p\)。也就是说，在不知道第一次选择结果的情况下，
\(P\{X_2 = 1\} = p\)
但是，在给定第一次选择的成员具备该特征的条件下，第二次选择的成员也具备该特征的条件概率为：
\(P\{X_2=1 | X_1=1\} = \frac{Np - 1}{N - 1}\)
于是我们可以注意到：如果第一次选择的成员具有该特征，那么第二次选择的成员可能是剩余的 \(N-1\) 个成员中具备该特征的 \(Np - 1\) 个成员中的任何一个。
类似的，在给定第一次选择的成员没有该特征的条件下，第二次选择的成员具有该特征的概率是：
\(P\{X_2=1 | X_1=0\} = \frac{Np}{N - 1}\)
因此，随机样本的第一个元素是否具有该特征会改变下一个元素具有该特征的概率。然而，当总体大小 \(N\) 远远超过样本大小 \(n\) 时，这种影响将会变得非常小。例如，如果 \(N=1000\)，\(p=0.4\)，于是有：
\(P\{X_2=1 | X_1=1\} = \frac{Np - 1}{N - 1} = \frac{399}{999} = 0.3994\)
\(P\{X_2=1 | X_1=0\} = \frac{Np}{N - 1} = \frac{400}{999} = 0.4004\)
如上的条件概率都和 \(P\{X_2 = 1\} = 0.4\) 非常接近。
事实上，可以证明，当总体规模 \(N\) 远大于样本大小 \(n\) 时，\(X_1, X_2, ..., X_n\) 之间近似于相互独立。现在，如果我们把每个 \(X_i\) 看作是一次试验的结果，如果 \(X_i\) 等于 1 则视为成功，否则视为失败。那么，\(X = \sum_{i=1}^{n}{X_i}\) 可以看作是 \(n\) 次试验中成功的总次数。因此，如果 \(X_i\) 是相互独立的，那么 \(X\) 将是一个参数为 \((n,p)\) 的二项随机变量。换句话说，当总体规模 \(N\) 远大于样本规模 \(n\) 时，样本中具有该特征的成员数量的分布近似于参数为 \((n,p)\) 的二项分布。
当然，\(X\) 是 小节 5.4 的超几何随机变量（hypergeometric random variable）。因此，之前的分析表明，当抽取的样本个数远小于总体规模时，超几何分布可以近似为二项分布。
对于本文的接下来的部分，我们将假设总体规模远大于样本大小，并且我们也将 \(X\) 的分布视为二项分布。
如 小节 5.1 中所述，对于一个二项随机变量而言，其均值和标准差分别为：
\(E[X] = np\)，\(\textup{Var}(X)=np(1-p)\)
则样本中具备某特征的成员的占比 \(\overline{X} = \frac{X}{n}\) 的均值和方差分别为：
\(E[\overline{X}] = \frac{E[X]}{n} = p\)
\(\textup{Var}(\overline{X}) = \frac{\textup{Var}(X)}{n^2} = \frac{p(1-p)}{n}\)
习题 6.7 在选举中，假设有 45% 的民众会支持某个候选人。如果选民的随机样本大小为 200，请计算：
解 6.7.
样本中支持该候选人的选民数量的期望和标准差为：
\(E[X] = np = 200 \cdot 0.45 = 90\)
\(SD(X) = \sqrt{np(1-p)} = \sqrt{200 \cdot 0.45 \cdot (1 - 0.45)} = 7.0356\)
因为 \(X\) 是一个参数为 \((200, 0.45)\) 的二项分布，因此：
\(P\{X \ge 101\} = 1 - P\{X \le 100\}\)
在 R 中，利用 1 - pbinom(100, 200, 0.45) 计算得：\(P\{X \ge 101\} = 0.06807525\)。
1 - pbinom(100, 200, 0.45)[1] 0.06807525\(\blacksquare\)
即使总体中每个元素都有两个以上的可能取值，如果总体规模远大于样本规模，那么样本数据仍然可以看作是来自总体分布的独立随机变量。
习题 6.8 根据美国农业部的《世界家畜状况》报告，丹麦是人均猪肉消费量最高的国家。2013 年，居住在丹麦的人的人均猪肉消费量均值为 147 磅，标准差为 62 磅。如果随机选择 25 名丹麦人作为样本，估算这 25 名丹麦人在 2013 年的平均猪肉消费量超过 150 磅的概率？
解 6.8. 令 \(X_i\) 表示样本中第 \(i\) 个人的猪肉消费量，\(i=1, ..., 25\)。则待求解的概率为：
\(P\bigg\{\frac{X_1 + \cdots + X_{25} }{25} \gt 150 \bigg\} = P\{\overline{X} \gt 150\}\)
其中，\(\overline{X}\) 为 25 个人的样本均值。我们可以将 \(X_i\) 看作是均值为 147、标准差为 62 的相互独立的随机变量。根据中心极限定理有：\(\overline{X}\) 是均值为 147、标准差为 \(\frac{62}{5}\) 的正态分布。用 \(Z\) 表示标准正态分布，则有：
\(P\{\overline{X} \gt 150\} = P\bigg\{\frac{\overline{X} - 147}{12.4} \gt \frac{150 - 147}{12.4} \bigg\}\)
\(P\{\overline{X} \gt 150\} \approx P\bigg\{Z \gt \frac{150 - 147}{12.4}\bigg\} = P\{Z \gt \frac{3}{12.4}\}\)
在 R 中，使用 pnorm(3/12.4, lower.tail = FALSE) 计算得到：
\(P\{\overline{X} \gt 150\} = 0.4044151\)
pnorm(3/12.4, lower.tail = FALSE)[1] 0.4044151\(\blacksquare\)
假设 \(X_1, X_2, X_3\) 是独立同分布的随机变量，其概率质量函数为：
\(P\{X_i = 0\} = 0.2\)，\(P\{X_i = 1\} = 0.3\)，\(P\{X_i = 3\} = 0.5\)
如果抛 10 个骰子，计算获得的点数（[10,60]）位于 \([30,40]\) 的近似概率？
计算 16 个独立、同 \((0,1)\) 均匀分布的随机变量的和超过 10 的概率？
在轮盘游戏中，轮盘有 38 个槽，编号分别为 0、00、1~36。如果你在指定的数字槽上押 1 点，当球落在这个数字槽上时你会赢 35 点，而当球没有落在这个数字槽上时你就会输 1 点。假设球会以相同的概率落在轮盘上的任何一个数字槽中，那么如果你不断的玩这个游戏，计算如下的概率：
一个公路部门有足够的盐来处理 80 英寸的降雪。假设每天的降雪的均值为 1.5 英寸、标准差为 3 英寸。
将 50 个数字四舍五入到最接近的整数后求和。如果四舍五入的误差是 -0.5 到 0.5 之间的均匀分布，估算得到的总和与实际总和相差超过 3 的概率。
一个六面的骰子，每个面出现的概率相等，反复抛这个骰子直到获得的总点数超过 400，估算总共抛的此处超过 140 次的概率？
某种电池的寿命是一个均值为 5 周、标准差为 1.5 周的随机变量。电池失效后会立即更换一块新的电池。估算一年内需要的电池数量大于或等于 13 的概率？
某种电气零件的寿命是一个均值为 100 小时、标准差为 20 小时的随机变量。如果测试 16 个零件，计算样本均值：
某烟草公司声称其香烟中的尼古丁含量是一个均值为 2.2 毫克、标准差为 0.3 毫克的随机变量。但是，随机选取的 100 个香烟样本的均值是 3.1 毫克。如果该公司的声称是真实的，那么样本均值大于或等于 3.1 毫克的概率是多少？
某种灯泡的寿命（小时）是一个均值为 500、标准差为 50 的随机变量。当样本大小为 \(n\) 时，估算样本均值超过 525 小时的概率？
一位老师根据经验了解到学生考试成绩的均值是 77、标准差是 15。如果该老师要教两个独立的班级，一个班级有 25 名学生，另一个有 64 名学生。
如果 \(X\) 是参数为 \((150,0.6)\) 的二项分布，计算 \(P\{X \ge 80\}\) 的确切值，并和如下的两种方式得到的概率进行对比：
1, 2, 3, 4 四支队伍中的每支队伍都将于其它的每一支队伍进行 10 次比赛。第 \(i\) 队和第 \(j\) 对比赛时，\(i\) 对获胜的概率是 \(P_{i,j}\)，\(j\) 对获胜的概率是 \(1 - P_{i,j}\)。如果： \(P_{1,2} = 0.6\) \(P_{3,1} = 0.7\) \(P_{2,3} = 0.6\) \(P_{4,2} = 0.75\) \(P_{3,4} = 0.5\) \(P_{4,1} = 0.5\)
一个篮球队每个赛季会打 60 场比赛。其中 32 场比赛是对阵甲级球队，28 场比赛是对阵乙级球队，并且所有比赛的结果都是独立的。每场比赛中，该队战 胜A 级对手的概率为 0.5，战胜 B 级对手的概率为 0.7。令 \(X\) 表示本赛季中该队的总胜利次数。
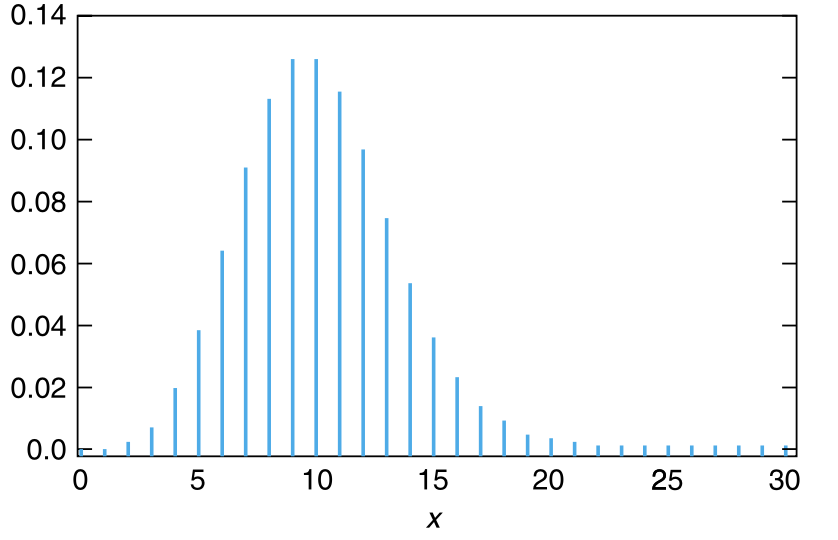
根据中心极限定理，当 \(\lambda\) 很大时，均值为 \(\lambda\) 的泊松分布将近似地具有均值和方差都等于 \(\lambda\) 的正态分布。如果 \(X\) 是均值为 100 的泊松随机变量，计算 \(X\) 小于或等于 116 的确切概率，并和如下的两种方式得到的概率进行对比：在近似正态分布中使用连续性校正；在近似正态分布中不使用连续性校正。泊松分布向正态分布的收敛参见 图 6.4。
\(X\) 是一个参数为 \((100, 0.1)\) 的二项随机变量，计算 \(P\{X \leq 10\}\)。将此分别与泊松逼近和正态逼近的结果进行比较（在使用正态逼近时，为了进行连续性校正，待求解的概率为 \(P\{X < 10.5\}\)）。
恒温器停止工作时的温度是服从方差为 \(\sigma^2\) 的正态分布。如果测试恒温器五次，计算：
其中 \(S^2\) 是五个测试数据值的样本方差。
在习题 18 中，样本的大小需要多大才能确保 \(P\{\frac{S^2}{\sigma^2} < 1.8 \}\) 至少为 0.95？
考虑两个独立的样本：第一个样本来自方差为 4 的正态分布，其大小为 10；第二个样本来自方差为 2 的正态分布，其大小为 5。计算第二个样本的方差超过第一个样本的方差的概率（提示：考虑使用 \(F-分布\)）。
12% 的人是左撇子。在一个 100 人的样本中，有 10 到 14 个左撇子的概率是多少？
某城市有 52% 的居民赞成在高中教授进化论。在一个大小为 \(n\) 的随机样本中，至少 50% 的人赞成教授进化论的概率是多少？
下表按照性别给出了某城市居民在健康习惯方面的相关数据。假设随机选择一个 300 名男性构成的样本，估算以下概率：
| 每晚睡眠不足 6 小时 (%) | 吸烟 (%) | 很少吃早餐 (%) | 体重超标 20% 以上 (%) | |
|---|---|---|---|---|
| 男性 | 22.7 | 28.4 | 45.4 | 29.6 |
| 女性 | 21.4 | 22.0 | 42.0 | 25.6 |
数据来源：美国国家健康统计，健康促进和疾病预防中心。
（使用习题 23 中的表格）假设随机选择一个 300 名女性构成的样本。估算以下概率：
（使用习题 23 中的表格）假设随机选择一个 300 名男性构成的样本和一个 300 名女性构成的样本。估算很少吃早餐的女性人数大于男性人数的概率。
下表使用数据来说明了青少年全职工人中、不同性别的年收入在不同薪资分组中的占比。假设选择 1000 名男性构成的样本和 1000 名女性构成的样本。使用表格来估算以下概率：
| 收入范围（单位：$） | 女性百分比 (%) | 男性百分比 (%) |
|---|---|---|
| 4999 或更少 | 2.8 | 1.8 |
| 5000 到 9999 | 10.4 | 4.7 |
| 10,000 到 19,999 | 41.0 | 23.1 |
| 20,000 到 24,999 | 16.5 | 13.4 |
| 25,000 到 49,999 | 26.3 | 42.1 |
| 50,000 及以上 | 3.0 | 14.9 |
来源：美国商务部，人口普查局。
如今，约 10.5% 的劳动者会加入工会。如果随机选择五名工人，他们加入工会的概率是多少？将你的答案与 1983 年 20.1% 的劳动这加入了工会这一数据进行比较。
旧金山所有学生在最近的数学学术能力测试中的样本均值和样本标准差分别是 517 和 120。估算 144 名学生构成的样本的平均得分超过以下值的概率：
化学工程专业的刚毕业的本科毕业生的平均工资为 53,600 美元，标准差为 3200 美元。估算 12 名刚毕业的化学工程师的平均工资超过 55,000 美元的概率。
某个元器件对电气系统的运行至关重要，一旦该元器件出现故障则必须立即更换。如果这种元件的平均寿命为 100 小时，并且其标准差为 30 小时，那么必须准备多少个该元器件，才能保障在接下来的 2000 小时内，系统持续运行的可能性至少为 0.95？(提示：令 \(X_i\) 表示第 \(i\) 个元器件的寿命)