代码
x <- c(2.2, 3.4, 1.6, 0.8, 2.7, 3.3, 1.6, 2.8, 2.5, 1.9)
log_x <- log(x)
mean_log_x <- mean(log_x)
sd_log_x <- sd(log_x)
print(mean_log_x)[1] 0.7504035代码
print(sd_log_x)[1] 0.4350637 参数估计
7.1 引言
令 \(X_1, ..., X_n\) 是来自分布为 \(F_\theta\) 的随机样本，这个分布由一个未知参数向量 \(\theta\) 来指定。例如，样本可能来自一个平均值未知的泊松分布；或者可能来自一个均值和方差都未知的正态分布。在概率论中，通常假设分布的所有参数都是已知的，而在统计学中，情况则恰恰相反。统计学的核心问题之一就是使用观测数据来推断未知参数。
- 在 小节 7.2 中，我们会介绍 最大似然方法（maximum likelihood）来估计未知参数。因为 最大似然估计 指定了一个单一值作为 \(\theta\) 的估计，因此我们称其为 点估计（point estimates）。
- 在 小节 7.3 中，我们会考虑 区间估计（interval estimates）的相关问题。对于区间估计而言，我们不会指定某个值作为 \(\theta\) 的估计，而是会指定一个区间来估计 \(\theta\)。此外，我们还考虑了可以对这样的区间估计报以多少 置信度（confidence）的问题。在该节中，我们会展示如何计算一个均值未知、但给定方差的正态分布的均值的区间估计。接下来，我们还会讨论区间估计中的一系列问题。在 小节 7.3.1 中，我们会讨论方差未知的正态分布的均值的区间估计。在 小节 7.3.2 中，我们会讨论正态分布的方差的区间估计。
- 在 小节 7.4 中，我们会讨论两个正态分布的均值差的区间估计，我们会分两种情况进行讨论：
- 这两个正态分布的方差是已知的；
- 这两个正态分布的方差未知，但是我们会假设他们的方差是相同的。
- 在 小节 7.5 和 小节 7.6 中，我们会分别讨论伯努利随机变量和指数随机变量的均值的区间估计。
- 在 小节 7.7 中，我们会重新回到计算未知参数的点估计的一般性问题上来，并展示如何通过 均方误差（mean square error）来评估估计量。我们还会讨论估计量的偏差，并会探讨偏差与均方误差之间的关系。
- 在 小节 7.8 中，我们会考虑在有先验信息可用时确定未知参数估计值的问题，这就是 贝叶斯（bayesian）方法。贝叶斯方法假设在观察数据之前，决策者总是可以获得关于 \(\theta\) 的信息，并且该信息可以用 \(\theta\) 的概率分布来表示。我们还会讨论如何使用估计量和参数 \(\theta\) 之间的均方误差来计算 贝叶斯估计量（Bayes estimator）。
估计量与估计值
在下一节会讲到：任何用于估计未知参数 \(\theta\) 的值的统计量都称为 \(\theta\) 的 估计量（estimator）。估计量的观测值称为 估计值（estimate）。
7.2 最大似然估计
任何用于估计未知参数 \(\theta\) 的值的统计量都称为 \(\theta\) 的 估计量（estimator）。估计量的观测值称为 估计值（estimate）。例如，一般而言，对于正态分布的均值的估计量是基于样本 \(X_1, ..., X_n\) 的样本均值 \(\overline{X} = \frac{\sum_i{X_i}}{n}\)。如果样本的大小为 3，并且样本数据为 \(X_1=2\)，\(X_2=3\)，\(X_3=4\)，那么根据估计量 \(\overline{X}\) 则得到总体均值的估计值 3。
假设随机变量 \(X_1, \ldots, X_n\) 的联合分布是已知的，只是有一个未知参数 \(\theta\)。我们关注的问题是使用观察到的值来估计 \(\theta\)。例如， \(X_i\) 可能是独立的指数随机变量，每个变量具有相同的未知均值 \(\theta\)。在这种情况下，随机变量的联合密度函数将由以下公式给出：
假设随机变量 \(X_1, ..., X_n\) 的联合分布是已知的，只是有一个未知的参数 \(\theta\)。我们关注的问题是：使用观察到的数据来估计 \(\theta\)。例如，\(X_i\) 可能是相互独立的指数随机变量，每个变量都具有相同的未知均值 \(\theta\)。在这种情况下，随机变量的联合密度函数为：
\[ \begin{align} f(x_1, x_2, ..., x_n) &= f_{X_1}(x_1) f_{X_2}(x_2) \cdots f_{X_n}(x_n) \\ &= \frac{1}{\theta}e^{-\frac{x_1}{\theta}} \frac{1}{\theta}e^{-\frac{x_2}{\theta}} \cdots \frac{1}{\theta}e^{-\frac{x_n}{\theta}} \\ &= \frac{1}{\theta^n}e^{-{\frac{\sum_{i=1}^{n}{x_i}}{\theta}}} \end{align} \]
我们的目标就是根据观测数据 \(x_1, x_2, ..., x_n\) 来估计 \(\theta\)。
在统计学中，一种被广泛使用的、特殊类型的估计量就是最大似然估计量（maximum likelihood estimator）。最大似然估计的推导过程如下。
- 令 \(f(x_1, ..., x_n | \theta)\) 表示随机变量 \(X_1, X_2, ..., X_n\) 的联合概率质量函数（当它们是离散随机变量时）或者联合概率密度函数（当它们是连续随机变量时）。因为我们假定 \(\theta\) 未知，所以我们也将 \(f\) 写成 \(\theta\) 的函数。
- 现在，\(f(x_1, ..., x_n | \theta)\) 表示当参数 \(\theta\) 是其真实值时，观测值为 \(x_1, x_2, ..., x_n\) 的可能性（likelihood）。因此，\(\theta\) 的合理的估计值应该是使得观测值的可能性最大的那个 \(\theta\) 值。
- 换句话说，最大似然估计 \(\hat{\theta}\) 就是令 \(f(x_1, ..., x_n | \theta)\) 取得最大值的 \(\theta\) 值，其中 \(x_1, ..., x_n\) 表示观侧数据。而函数 \(f(x_1, ..., x_n | \theta)\) 也被称为关于 \(\theta\) 的似然函数。
- 为了确定 \(f(x_1, ..., x_n | \theta)\) 最大时的 \(\theta\) 值，通常会利用以下的事实：函数 \(f(x_1, ..., x_n | \theta)\) 和函数 \(\textup{log}[f(x_1, ..., x_n | \theta)]\) 取得最大值时的 \(\theta\) 值是相同的。因此，我们也可以通过最大化 \(\textup{log}[f(x_1, ..., x_n | \theta)]\) 得到 \(\hat{\theta}\)。
习题 7.1 伯努利分布参数的最大似然估计。假设执行 \(n\) 个独立试验，每个试验的成功概率均为 \(p\)。则 \(p\) 的最大似然估计是多少？
解 7.1. 观察数据由 \(X_1, ..., X_n\) 的值构成，其中 \(X_i = \begin{cases} 1, \quad & 第 i 次试验成功\\ 0, \quad & 其它 \end{cases}\)
令 \(P\{X_i = 1\} = p = 1- P\{X_i = 0\}\)，该等式可以简化为：
\(P\{X_i = x\} = p^x(1-p)^{1-x}, \quad x = 0,1\)
因此试验之间相互独立，因此观察到的数据的可能性（likelihook，指的就是联合概率质量函数）为：
\(\begin{align} f(x_1, ..., x_n | p) &= P\{X_1 = x_1, ..., X_n = x_n | p\} \\ &= p^{x_1}(1-p)^{1-x_1} \cdots p^{x_n}(1-p)^{1-x_n} \\ &= p^{\sum_{i=1}^{n}{x_i}} (1-p)^{n - \sum_{i=1}^{n}{x_i}}, \quad x_i = 0,1, \quad i = 1,...,n \end{align}\)
为了确定是的 \(f\) 取得最大值时 \(p\) 的值，首先对 \(f\) 取对数： \(\textup{log}f(x_1, ..., x_n | p) = \bigg(\sum_{i=1}^{n}{x_i}\bigg)\textup{log}\ p +\bigg (n - \sum_{i=1}^{n}{x_i}\bigg)\textup{log}(1 - p)\)
求导得到：
\(\frac{d}{dp} \textup{log}\ f(x_1, ..., x_n | p) = \frac{\sum_{i=1}^{n}{x_i}}{p} -\frac{n - \sum_{i=1}^{n}{x_i}}{1-p}\)
令 \(\frac{d}{dp} \textup{log}\ f(x_1, ..., x_n | p) = 0\) 并计算得到最大似然估计 \(\hat{p}\) 满足：
\(\frac{\sum_{i=1}^{n}{x_i}}{\hat{p}} -\frac{n - \sum_{i=1}^{n}{x_i}}{1-\hat{p}}\)
即，\(\hat{p} = \frac{\sum_{i=1}^{n}{x_i}}{n}\)
因此，均值未知的伯努利分布的最大似然估计量为：
\(d(X_1, ..., X_n) = \frac{\sum_{i=1}^{n}{X_i}}{n}\)
因为 \(\sum_{i=1}^{n}{X_i}\) 就是试验成功的次数，所以 \(p\) 的最大似然估计就等于观察到的实验中成功次数的占比。举个例子，假设某制造商生产的 每个 RAM（运行内存）芯片的合格率是相互独立的，并且合格率为 \(p\)。如果在 1000 个测试样本中，有 921 个合格品，那么 \(p\) 的最大似然估计是 0.921。 \(\blacksquare\)
习题 7.2 两位编辑审验相同的一本稿件，如果第一位编辑发现 \(n_1\) 个错误，第二位编辑发现 \(n_2\) 个错误，其中有 \(n_{1,2}\) 个错误两位编辑都发现了，估计这本稿件中的错误总数 \(N\)。
解 7.2. 在估计 \(N\) 之前，需要对潜在的概率模型做一些假设。假设不同编辑的审验结果之间是独立的，并且稿件中的每个错误被第 \(i\) 位编辑独立发现的概率为 \(p_i,\ i = 1,2\)。
为了估计 \(N\)，我们将从推导 \(p_1\) 的估计量开始。为此，请注意，第一位编辑将会以 \(p_1\) 的概率独立发现第二位编辑发现的 \(n_2\) 个错误中的每一个错误。因为第一位编辑发现了\(n_2\) 个错误中的 \(n_{1,2}\) 个错误，因此，\(p_1\) 的合理估计为：
\(\hat{p}_1 = \frac{n_{1,2}}{n_2}\)
但是，对于稿件中的 \(N\) 个错误，因为第一位编辑发现了其中的 \(n_1\) 个错误，因此假设 \(p_1\) 近似的等于 \(\frac{n_1}{N}\) 也是合理的。因此 \(\hat{p}_1 \approx \frac{n_1}{N}\)，即 \(\frac{n_{1,2}}{n_2}\approx \frac{n_1}{N}\)，也就是说：
\(N \approx \frac{n_1 n_2}{n_{1,2}}\)
因为如上的估计对于 \(n_1\) 和 \(n_2\) 是对称的，所以无论哪个编辑是第一位编辑，最终的结果都是相同的。
当两个研究小组宣布他们已经破译了人类遗传密码序列时，如上估计过程的一个有趣的案例发生了。作为两个研究小组工作的一部分，他们都估计人类基因组由大约 33000 个基因组成。因为这个数字是由两个小组独立得出的，许多科学家认为这个数字是可信的。但是，大多数科学家对这个相对较少的基因数量感到非常惊讶；相比之下，它只是果蝇基因数量的两倍左右。然而，对两个小组的研究结果进行更为仔细的检查表明，这两个小组均发现的基因数量大约为 17000 个（也就是说，有 17000 个相同的基因被这两个小组发现了）。因此，根据我们之前的估计量，我们会估计基因的实际数量不是 33000个，而是 \(\frac{n_1 n_2}{n_{1,2}} = \frac{33000 \times 33000}{17000} \approx 64000\) 个。
对于声称发现的基因中的某些基因是否真的存在会有一些争议，因此，64000个基因应该被视为基因实际数量的上限。
当有 \(m(m \gt 2)\) 个编辑时，则上述采用的两位编辑的估计方法将不再适用。
当 \(m \gt 2\) 时，对于第 \(i\) 为编辑，我们令 \(\hat{p}_i\) 为由至少一位其他编辑 \(j(j \ne i)\) 发现的错误中 \(i\) 也发现的错误的占比，然后让 \(\hat{p}_i\) 等于 \(\frac{n_i}{N}\)，那么 \(N\) 的估计值，即 \(\frac{n_i}{\hat{p}_i}\)，将因不同的 \(i\) 而异。
此外，使用这种方法时，即使第 \(i\) 位编辑找到的错误比第 \(j\) 位编辑的少，我们也有可能得到 \(\hat{p}_i > \hat{p}_j\)。例如，对于 \(m = 3\)，假设第 1 位编辑和第 2 位编辑找到了完全相同的 10 个错误，而第 3 位编辑找到了 20 个错误且只有 1 个与其他编辑找到的错误是相同的。因为第 1 位编辑和第 2 位编辑都找到了 29 个错误中的 10 个（第 2 位编辑和第 3 位编辑总共找到了 29 个不同的错误），所以，\(\hat{p}_i = \frac{10}{29}\)，\(i = 1, 2\)。另一方面，因为第 3 位编辑仅找到了其他编辑找到的 10 个错误（第 1 位编辑和第 2 为编辑找到的 10 个错误是相同的）中的 1 个，因此 \(\hat{p}_3 = \frac{1}{10}\)。因此，尽管第 3 位编辑找到的错误是 第 1 位编辑的两倍，但 \(p_3\) 的估计值小于 \(p_1\) 的估计值。
为了获得更合理的估计，我们可以将上述 \(\hat{p}_i,\ i=1, ..., m\) 值作为 \(p_i\) 的初步估计值。现在，令 \(n_f\) 为至少由一位编辑发现的错误的数量。因为至少一位编辑发现的错误的占比为 \(\frac{n_f}{N}\)，因此 \(\frac{n_f}{N}\) 近似等于某个错误至少被一位编辑发现的概率 \(1 - \Pi_{i=1}^{m}{(1 - p_i)}\)。因此，有：
\(\frac{n_f}{N} \approx 1 - \Pi_{i=1}^{m}{(1-p_i)}\)
假设 \(N \approx \hat{N}\)，有：
\[ \hat{N} = \frac{n_f}{1 - \Pi_{i=1}^{m}{(1-\hat{p_i})}} \tag{7.1}\]
有了 \(N\) 的估计，我们可以通过 \(N\) 的估计来重新估计 \(p_i\)：
\[ \hat{p_i} = \frac{n_i}{\hat{N}}, \quad i = 1, ..., m \tag{7.2}\]
然后，我们可以根据新的 \(\hat{p_i}\) 并利用 式 7.1 重新估计 \(N\)。注意，估计的过程不应该就此停止，每当我们获得了 \(N\) 的新估计 \(\hat{N}\) 时，我们可以利用 式 7.2 获得 \(p_i\) 的新估计，然后可以使用 \(p_i\) 的新估计来获得 \(N\) 的新估计，依此类推。） \(\blacksquare\)
习题 7.3 泊松分布参数的最大似然估计。假设 \(X_1, ..., X_n\) 是独立的泊松随机变量，其均值为 \(\lambda\)。确定 \(\lambda\) 的最大似然估计量。
解 7.3. \(\lambda\) 的似然函数为：
\(\begin{align} f(x_1, ..., x_n | \lambda) &= \frac{\lambda^{x_1}e^{-\lambda}}{x_1!} \cdots \frac{\lambda^{x_n}e^{-\lambda}}{x_n!} \\ &= \frac{\lambda^{\sum_{i=1}^{n}{x_i}}e^{-n\lambda}}{x_1! \cdots x_n!} \end{align}\)
对上式取对数有：
\(\textup{log}\ f(x_1, ..., x_n | \lambda) = -n\lambda + \sum_{i=1}^{n}{x_i} \textup{log}\ \lambda - \textup{log}\ c\)
其中，\(c = \Pi_{i=1}^{n}{x_i!}\)，对上式求导有：
\(\frac{d}{d\lambda} \textup{log}\ f(x_1, ..., x_n | \lambda) = -n + \frac{1}{\lambda} \sum_{i=1}^{n}{x_i}\)
令上式为 0，得到最大似然估计 \(\hat{\lambda} = \frac{\sum_{i=1}^{n}{x_i}}{n}\)
因此，最大似然估计量为：
\(d(X_1, ..., X_n) = \frac{\sum_{i=1}^{n}{x_i}}{n}\)
例如，假设任何一天进入某个零售店的人数是一个泊松随机变量，其均值 \(\lambda\) 未知，我们希望估计 \(\lambda\) 的值。如果 20 天后，共有857 人进入该机构，那么 \(\lambda\) 的最大似然估计为 \(\frac{857}{20}=42.85\)。也就是说，平均而言，我们估计在给定的一天将有 42.85 名顾客进入该零售店。\(\blacksquare\)
习题 7.4 1998 年加州伯克利市在 10 个随机选择的非雨天发生的交通事故数量如下：
4,0,6,5,2,1,2,0,4,3
使用这些数据来估计非雨天最多发生 2 起交通事故的天数占比。
解 7.4. 由于有大量司机，并且每个司机在某一天发生事故的可能性很小，因此假设每天的交通事故数量是泊松随机变量似乎是合理的。因为 \(\overline{X} = \frac{1}{10} \sum_{i=1}^{10}{X_i} = 2.7\)，因此，泊松分布的均值的最大似然估计值为 2.7。最多发生 2 起事故的非雨天的长期占比等于 \(P\{X \le 2\}\)，其中 \(X\) 表示一天中的事故数。因此待计算的估计值为：
\(\begin{align} P\{X \le 2\} &= P\{X = 0\} + P\{X = 1\} + P\{X = 2\} \\ &= e^{-2.7}(1 + 2.7 + \frac{{2.7}^2}{2}) \\ &= 0.4936 \end{align}\)
也就是说，我们估计有不到一半的非雨天最多发生 2 起事故。\(\blacksquare\)
习题 7.5 正态分布总体的最大似然估计。假设 \(X_1, ..., X_n\) 是相互独立的正态分布随机变量，其均值 \(\mu\) 和标准差 \(\sigma\) 均未知。计算其均值和标准差的最大似然估计。
解 7.5. 其联合概率密度函数为：
\(\begin{align} f(x_1, ..., x_n | \mu, \sigma) &= \Pi_{i=1}^{n}{\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x_i - \mu)^2}{2\sigma^2}}} \\ &= (\frac{1}{2\pi})^{\frac{n}{2}} \frac{1}{\sigma^n} e^{\frac{-\sum_{i=1}^{n}{(x_i - \mu)^2}}{2\sigma^2}} \end{align}\)
取对数有：
\(\textup{log}\ f(x_1, ..., x_n | \mu, \sigma) = - \frac{n}{2} \textup{log}\ (2\pi) - n \textup{log}\ \sigma - \frac{\sum_{i=1}^{n}{(x_i - \mu)^2}}{2 \sigma^2}\)
为了找到 \(\mu\) 和 \(\sigma\) 以使上述值最大化，我们计算如下的偏导数：
\(\frac{\partial}{\partial \mu} \textup{log}\ f(x_1, ..., x_n | \mu, \sigma) = \frac{\sum_{i=1}^{n}{(x_i - \mu)}}{\sigma^2}\)
\(\frac{\partial}{\partial \sigma} \textup{log}\ f(x_1, ..., x_n | \mu, \sigma) = - \frac{n}{\sigma} + \frac{\sum_{i=1}^{n}{(x_i - \mu)^2}}{\sigma^3}\)
令如上的偏导数等于 0，有：
\(\hat{\mu} = \frac{\sum_{i=1}^{n}{x_i}}{n}\)
\(\hat{\sigma} = \bigg[\frac{\sum_{i=1}^{n}{(x_i - \hat{\mu})^2}}{n}\bigg]^{\frac{1}{2}}\)
因此，正态分布的均值和标准差的最大似然估计量分别为：
\[ \begin{align} \hat{\mu} &= \overline{X} \\ \hat{\sigma} &= \bigg[\frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{n}\bigg]^{\frac{1}{2}} \end{align} \tag{7.3}\]
需要注意的是：标准差 \(\sigma\) 的最大似然估计并不等同于样本标准差：
\(S = \bigg[\frac{\sum_{i=1}^{n}{(X_i - \overline{X})^2}}{n - 1}\bigg]^{\frac{1}{2}}\)
在 式 7.3 中，分母为 \(\sqrt{n}\)，而不是样本方差中的 \(\sqrt{n - 1}\)。然而，对于合理大小的 \(n\)，\(\sigma\) 的这两个估计量将近似相等。\(\blacksquare\)
习题 7.6 Kolmogorov 碎裂定律（Kolmogorov’s law of fragmentation）指出，由矿物化合物碎裂产生的大量颗粒中的单个颗粒的大小服从近似对数正态分布（lognormal distribution）。如果一个随机变量 \(X\) 的对数 \(\textup{log}\ (X)\) 服从正态分布，那么 \(X\) 则具有对数正态分布。碎裂定律最初是通过实验证明的，后来由 Kolmogorov 提供了理论基础，并被应用于各种工程研究。例如，人们用碎裂定律来分析从一堆金砂中随机挑选出的颗粒的大小。碎裂定律还应用与地震断裂带的应力释放研究中（参见：Lomnitz, C., “Global Tectonics and Earthquake Risk,” Developments in Geotectonics, Elsevier, Amsterdam, 1979）。
假设从一大堆金属砂中取出 10 粒样品，它们的长度（以毫米为单位）分别是：
2.2, 3.4, 1.6, 0.8, 2.7, 3.3, 1.6, 2.8, 2.5, 1.9
估计整个砂堆中长度在 2~3 毫米之间的砂粒的百分比。
解 7.6. 取这 10 个数据值的自然对数，得到转换后的数据集结果：
0.7885, 1.2238, 0.4700, -0.2231, 0.9933, 1.1939, 0.4700, 1.0296, 0.9163, 0.6419
因为如上数据的样本均值和样本标准差分别为：
\(\overline{x} = 0.7504, s = 0.4351\)
因此，随机选择的砂粒长度的对数服从均值为 0.7504、标准差为 0.4351 正态分布。所以，如果 \(X\) 是砂粒的长度，那么
\(\begin{align} P\{2 \lt X \lt 3\} &= P\{\textup{log}\ 2 \lt \textup{log}\ X \lt \textup{log}\ 3\} \\ &= P\bigg\{\frac{\textup{log}\ 2 - 0.7504}{0.4351} \lt \frac{\textup{log}\ X - 0.7504}{0.4351} \lt \frac{\textup{log}\ 3 - 0.7504}{0.4351}\bigg\} \\ & \approx pnorm(\textup{log}\ 3 - 0.7504 / 0.4351) - pnorm(\textup{log}\ 2 - 0.7504 / 0.4351) \\ &= 0.3405766 \end{align}\)
代码
pnorm((log(3) - 0.7504) / 0.4351) - pnorm((log(2) - 0.7504) / 0.4351)[1] 0.3405766\(\blacksquare\)
当随机变量可以看作大量独立、同分布的随机变量的乘积的情况下，我们可以假设该随机变量服从对数正态分布。例如，在金融领域，经常用对数正态分布来估计股价在未来某段时间的价格分布。为了理解这种假设的合理性，我们假设当前股价是 \(s\)，我们关心的是经过时间 \(t\) 后的股票价格 \(S(t)\)。对于一个较大的 \(n\) 值，令 \(t_i = \frac{t}{n}\)，并令 \(S(t_1), S(t_2), ..., S(t_n)\) 表示在时间 \(t_1, t_2, ..., t_n\) 时的股价。金融领域中的一个比较常见的假设是：\(\frac{S(t_i)}{S(t_{i-1})}\) 近似符合独立同分布。因此，如果我们令 \(X_i = \frac{S(t_i)}{S(t_{i-1})}\)，则：
\(\begin{align} S(t) = S(t_n) &= S(t_0) \cdot \frac{S(t_1)}{S(t_0)} \cdot \frac{S(t_2)}{S(t_1)} \cdot \cdots \cdot \frac{S(t_n)}{S(t_{n-1})} \\ &= s \prod_{i=1}^{n} X_i \end{align}\)
对上式取对数得：
\(\log(S(t)) = \log(s) + \sum_{i=1}^{n} \log(X_i)\)
根据中心极限定理有：\(\log(S(t))\) 将近似服从正态分布。
已经证明，对于某些随机变量而言，对数正态分布是一个很好的拟合，例如病人的住院时长和车辆的行驶时间。
提示
在上述所有例子中，总体均值的最大似然估计都是样本均值 \(\overline{X}\)。但是并非所有情况都是如此，例如 例 7.1。
例 7.1 均匀分布的均值的最大似然估计。假设 \(X_1, ..., Xn\) 是来自均匀分布 \((0, \theta)\) 的样本，其中 \(\theta\) 未知。因此，\(X_i\) 的联合密度函数为：
\(f(x_1, x_2, ..., x_n | \theta) = \begin{cases} \frac{1}{\theta^n}, \quad & 0 \lt x_i \lt \theta \\ 0, \quad & 其它 \end{cases}\)
如果 \(\theta\) 尽可能小，则 \(f(x_1, x_2, ..., x_n | \theta)\) 则会尽可能的大。由于 \(\theta\) 必须至少与所有观测值 \(x_i\) 一样大，因此 \(\theta\) 的最小的可能值等于 \(max(x_1, x_2, ..., x_n)\)。因此，\(\theta\) 的最大似然估计量是
\(\hat{\theta} = max(X_1, X_2, ..., X_n)\)
因此，可以得出均匀分布均值 \(\frac{\theta}{2}\) 的最大似然估计量为 \(\frac{max(X_1, X_2, ..., X_n)}{2}\)。\(\blacksquare\)
7.2.1 估计寿命分布
从今天出生的孩子中随机选择一个样本，令 \(X\) 表示样本中的孩子死亡时的年龄。若新生儿在其第 \(i\) 年死亡，则 \(X = i\)，\(i \geq 1\)。为了估计 \(X\) 的概率质量函数，令 \(\lambda_i\) 表示一个新生儿在度过其第 \(i - 1\) 年后在第 \(i\) 年死亡的概率。即，
\(\lambda_i = P\{X = i | X > i - 1\} = \frac{P\{X = i\}}{P\{X > i - 1\}}\)
另外，令
\(s_i = 1 - \lambda_i = \frac{P\{X > i\}}{P\{X > i - 1\}}\)
表示新生儿在度过其前 \(i - 1\) 年后在第 \(i\) 年仍然健在的概率。我们称 \(\lambda_i\) 为故障率（failure rate），称 \(s_i\) 为生存率（survival rate）（个体在第 \(i\) 年的生存概率）。现在，
\(s_1 s_2 \cdots s_i = P\{X > 1\} \frac{P\{X > 2\}}{P\{X > 1\}} \frac{P\{X > 3\}}{P\{X > 2\}} \cdots \frac{P\{X > i\}}{P\{X > i - 1\}} = P\{X > i\}\)
因此，
\(P\{X = n\} = P\{X > n - 1\} \lambda_n = s_1 \cdots s_{n - 1} (1 - s_n)\)
因此，我们可以通过估计 \(s_i, i = 1, \ldots, n\) 来估计 \(X\) 的概率质量函数。\(s_i\) 可以通过查看所有在第 \(i-1\) 年健在的人在第 \(i\) 年仍然健在的人来估计 \(s_i\) 的值，其估计值 \(\hat{s}_i\) 为他们今天仍然健在的比例。然后我们将使用 \(\hat{s}_1 \hat{s}_2 \cdots \hat{s}_{n - 1} (1 - \hat{s}_n)\) 来估计 \(P\{X = n\}\)。（注意，尽管我们在估计 \(s_i\) 时使用了尽可能最新的数据，但我们对新生儿寿命的概率质量函数的估计是假设新生儿在达到年龄 \(i\) 时的生存率与去年同年龄 \(i\) 的人的生存率相同。）
在健康研究中，使用生存率来估计寿命分布也是很重要的，尤其是在信息不完全的情况下。例如，考虑一项研究，其中一种新药物被给与 12 名肺癌患者。假设一段时间后，我们得到了从开始服用新药到患者死亡的月份数：
\(4, 7^*, 9, 11^*, 12, 3, 14^*, 1, 8, 7, 5, 3^*\)
其中 \(x\) 表示患者在开始复用新药后的第 \(x\) 个月死亡，而 \(x^*\) 表示患者服药 \(x\) 个月并且仍然健在。
令 \(X\) 表示开始复用新药后的生存月份数，并令
\(s_i = P(X > i \mid X > i - 1) = \frac{P(X > i)}{P(X > i - 1)}\)
为了估计 \(s_i\)，即在第 \(i - 1\) 个月存活的患者也将在第 \(i\) 个月存活的概率，我们应该取那些在第 \(i\) 个月开始服药并且在这个月存活的患者的比例。例如，因为 12 名患者中有 1 名在第 1 个月后死亡，所以 \(\hat{s}_1 = \frac{11}{12}\)。因为所有在第 2 个月开始服药的 11 名患者都存活，所以 \(\hat{s}_2 = \frac{11}{11}\)。因为 11 名患者中有 1 名在第 3 个月后死亡，所以 \(\hat{s}_3 = \frac{10}{11}\)。因为 9 名患者中，有 1 名在第 4 个月后死亡，所以 \(\hat{s}_4 = \frac{8}{9}\)。类似的推理适用于其他月份，于是得到以下生存率估计值：
\(\hat{s}_1 = \frac{11}{12}\)
\(\hat{s}_2 = \frac{11}{11}\)
\(\hat{s}_3 = \frac{10}{11}\)
\(\hat{s}_4 = \frac{8}{9}\)
\(\hat{s}_5 = \frac{7}{8}\)
\(\hat{s}_6 = \frac{7}{7}\)
\(\hat{s}_7 = \frac{6}{7}\)
\(\hat{s}_8 = \frac{4}{5}\)
\(\hat{s}_9 = \frac{3}{4}\)
\(\hat{s}_{10} = \frac{3}{3}\)
\(\hat{s}_{11} = \frac{3}{3}\)
\(\hat{s}_{12} = \frac{1}{2}\)
\(\hat{s}_{13} = \frac{1}{1}\)
\(\hat{s}_{14} = \frac{1}{1}\)
现在，我们可以使用 \(\prod_{i=1}^j \hat{s}_i\) 来估计服用新药至少存活 \(j\) 个月的概率，其中 \(j = 1, \ldots, 14\)。例如，\(P\{X > 6\}\) 的估计是 \(\frac{35}{54}\)。
7.3 区间估计
假设 \(X_1, \ldots, X_n\) 是来自均值 \(\mu\) 未知但是方差 \(\sigma^2\) 已知的正态分布总体的样本。根据 小节 7.2，我们知道 \(\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i\) 是 \(\mu\) 的最大似然估计。然而，我们不能指望样本均值 \(\overline{X}\) 会正好等于 \(\mu\)，我们反而更希望 \(\overline{X}\) 会“接近” \(\mu\)。因此，有时指定一个 \(\mu\) 可能会落入的、我们有一定信心水平的区间，比一个点估计更有价值。为了得到这样的区间估计量，我们需要利用点估计量的概率分布。
如 小节 6.2 所述，点估计量 \(\overline{X}\) 服从均值为 \(\mu\) 、方差为 \(\frac{\sigma^2}{n}\) 的正态分布，因此：
\(\frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}} = \sqrt{n} \frac{(\overline{X} - \mu)}{\sigma}\)
服从标准正态分布。因此，
\(P\bigg\{ -1.96 < \sqrt{n} \frac{(\overline{X} - \mu)}{\sigma} < 1.96 \bigg\} = 0.95\)
上式等价于：
\(P\bigg\{ -1.96 \frac{\sigma}{\sqrt{n}} < \overline{X} - \mu < 1.96 \frac{\sigma}{\sqrt{n}} \bigg\} = 0.95\)
通过乘以 -1 得到等价的表述：
\(P\bigg\{ -1.96 \frac{\sigma}{\sqrt{n}} < \mu - \overline{X} < 1.96 \frac{\sigma}{\sqrt{n}} \bigg\} = 0.95\)
即，
\(P\bigg\{ \overline{X} - 1.96 \frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.96 \frac{\sigma}{\sqrt{n}} \bigg\} = 0.95\)
也就是说，样本均值 \(\overline{X}\) 有 95% 的概率落在与总体均值 \(\mu\) 之间的距离小于 \(1.96 \frac{\sigma}{\sqrt{n}}\) 的区间。如果我们现在观察样本，并且发现 \(\overline{X} = \overline{x}\)，那么我们可以说，有 95% 的置信度使得
\[ \overline{x} - 1.96 \frac{\sigma}{\sqrt{n}} < \mu < \overline{x} + 1.96 \frac{\sigma}{\sqrt{n}} \tag{7.4}\]
也就是说，我们“有95%的信心”断言总体的均值位于观测到的样本均值的 \(\pm 1.96\) 个标准差的区间内。（需要注意到，\(\overline{X}\) 的标准差为 \(\frac{\sigma}{\sqrt{n}}\)）。
我们称
\(\left( \overline{x} - 1.96\frac{\sigma}{\sqrt{n}},\ \overline{x} + 1.96\frac{\sigma}{\sqrt{n}}\right)\)
为 \(\mu\) 的 95% 置信区间估计（95 percent confidence interval estimate of \(\mu\) ）。
习题 7.7 假设从 A 地发射一个信号 \(\mu\) 到 B 地，在 B 接收到的信号的值服从均值为 \(\mu\)、方差为 4 的正态分布。也就是说，如果发送的信号值为 \(\mu\)，那么接收到的信号值是 \(\mu + N\)，其中 \(N\) 代表噪声是服从均值为 0、方差为 4 的正态分布。为了减少误差，相同的值会被发送 9 次。如果接收到的值分别是：
5、8.5、12、15、7、9、7.5、6.5、10.5
为 \(\mu\) 构造一个 95% 置信区间。
解 7.7. 因为 \(\overline{x} = \frac{81}{9} = 9\)，因此，假设 B 地接收到的信号值之间是独立的，则 \(\mu\) 的 95% 可信区间是：
\(\left(9 - 1.96\frac{\sigma}{3},\ 9 + 1.96\frac{\sigma}{3}\right) = (7.69, 10.31)\)
因此，我们有 95% 的置信度确认真实的信号值将位于 7.69~10.31 的范围内。
式 7.4 中的区间称为双边置信区间（two-sided confidence interval）。然而，有时我们感兴趣的是确定一个值，使得我们能以 95% 的置信度断言 \(\mu\) 至少与该值一样大。
如果 \(Z\) 是一个标准正态分布随机变量，则
\(P\{Z \lt 1.645\} = 0.95\)
注记
在 R 中，可以使用 qnorm() 来得到该值：
代码
qnorm(0.95)[1] 1.644854因此有：\(P\bigg\{\sqrt{n}\frac{(\overline{X} - \mu)}{\sigma} \lt 1.645\bigg\} = 0.95\)，即
\(P\bigg\{\overline{X} - 1.645\frac{\sigma}{\sqrt{n}} \lt \mu \bigg\} = 0.95\)
因此，\(\mu\) 的 95% 单边上置信区间为：
\(\left(\overline{x} - 1.645\frac{\sigma}{\sqrt{n}},\ \infty\right)\)，其中 \(\overline{x}\) 为观察到的数据的样本均值。
注记
或者说，我们有 95% 的信心认为 \(\mu\) 的值不可能低于 \(\overline{x} - 1.645\frac{\sigma}{\sqrt{n}}\)。
类似的，我们可以得到单边下置信区间（one-sided lower confidence interval）。当我们观察到的数据的样本均值为 \(\overline{x}\) 时，则 \(\mu\) 的 95% 单边下置信区间为：
\(\left(-\infty,\ \overline{x} + 1.645\frac{\sigma}{\sqrt{n}}\right)\)
注记
或者说，我们有 95% 的信心认为 \(\mu\) 的值不可能大于 \(\overline{x} + 1.645\frac{\sigma}{\sqrt{n}}\)。
习题 7.8 确定 习题 7.7 中 \(\mu\) 的 95% 置信区间估计的上下限。
解 7.8. 因为：
\(1.645 \frac{\sigma}{\sqrt{n}} = \frac{3.29}{3} = 1.097\)，
所以，95% 上置信区间为：\((9 - 1.097, \infty) = (7.903, \infty)\)。 95% 下置信区间为：\((-\infty, 9 + 1.097) = (-\infty, 10.097)\)。\(\blacksquare\)
我们也可以获得任何指定置信水平的置信区间。为此，回忆一下 \(z_{\alpha}\) 的定义。\(z_{\alpha}\) 是使得
\[ P\{Z > z_{\alpha}\} = \alpha \]
成立的值，其中 \(Z\) 是标准正态随机变量。这意味着（见 图 7.1），对于任意 \(\alpha\)，
\[ P\{-z_{\alpha/2} < Z < z_{\alpha/2}\} = 1 - \alpha \]
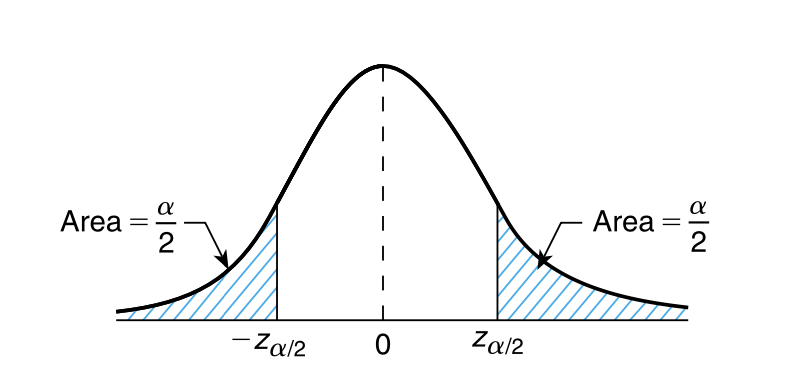
因此，我们有：
\[ P\left\{ -z_{\alpha/2} < \sqrt{n}\left(\frac{\overline{X} - \mu}{\sigma}\right) < z_{\alpha/2} \right\} = 1 - \alpha \]
或
\[ P\left\{ -z_{\alpha/2} \frac{\sigma}{\sqrt{n}} < \overline{X} - \mu < z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \right\} = 1 - \alpha \]
或
\[ P \left\{-z_{\alpha/2} \frac{\sigma}{\sqrt{n}} < \mu - \overline{X} < z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\right\} = 1 - \alpha \]
也就是说，
\[ P \left\{\overline{X} - z_{\alpha/2} \frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\right\} = 1 - \alpha \]
因此，\(\mu\) 的 \(100(1−\alpha)％\) 的双边置信区间是：
\[ \left(\overline{X} - z_{\alpha/2} \frac{\sigma}{\sqrt{n}}, \overline{X} + z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\right) \]
其中 \(\overline{X}\) 是观测样本均值。
同样地，对于一个标准正态随机变量 \(Z = \sqrt{n} \frac{(\overline{X} - \mu)}{\sigma}\)，有 \(P\{Z > z_{\alpha}\} = \alpha\) 和 \(P\{Z < -z_{\alpha}\} = \alpha\)。
因此，我们可以得到任意置信水平的单边置信区间。具体来说，\(\mu\) 的 \(100(1−\alpha)％\) 单边上置信区间和 \(100(1−\alpha)％\) 单边下置信区间分别为：
- \(\left(\overline{X} - z_{\alpha} \frac{\sigma}{\sqrt{n}}, \infty\right)\)
- \(\left(-\infty, \overline{X} + z_{\alpha} \frac{\sigma}{\sqrt{n}}\right)\)
习题 7.9 使用 习题 7.7 中的数据来计算 \(\mu\) 的 99% 置信区间估计，以及其 99% 单边上、下置信区间。
解 7.9. 由于 \(z_{0.005} = 2.58\)，且 \(2.58 \frac{\sigma}{\sqrt{n}} = \frac{5.16}{3} = 1.72\)，
因此，\(\mu\) 的 99% 置信区间为 \(9 \pm 1.72\)，也就是说，99% 置信区间估计为 \((7.28, 10.72)\)。
此外，由于 \(z_{0.01} = 2.33\)，因此，99% 上置信区间为 \((9 - 2.33(\frac{2}{3}), \infty) = (7.447, \infty)\)。
同样地，99% 下置信区间为 \((-\infty, 9 + 2.33(\frac{2}{3})) = (-\infty, 10.553)\)。\(\blacksquare\)
有时候，我们对某一置信水平（比如 \(1−\alpha\)）的双边置信区间感兴趣，但问题是如何选择样本量 \(n\) 才能使得置信区间为某个指定的大小。例如，假设我们要计算一个长度为 0.1 的区间，并且能断言该区间以 99% 的置信度包含 \(\mu\)，此时我们需要多大的样本量 \(n\)？
由于 \(z_{0.005} = 2.58\)，从样本量为 \(n\) 的样本中得到的 \(\mu\) 的 99% 置信区间是：
\(\left( \overline{X} - 2.58 \frac{\sigma}{\sqrt{n}}, \overline{X} + 2.58 \frac{\sigma}{\sqrt{n}} \right)\)
因此，置信区间的长度为：\(5.16 \frac{\sigma}{\sqrt{n}}\)。因此，要使置信区间的长度等于 0.1，我们必须让 \(5.16 \frac{\sigma}{\sqrt{n}} = 0.1\)，即：\(n = (51.6 \sigma)^2\)。
注意
对“\(100(1−\alpha)％\) 置信区间”的解释可能会令人困惑。需要注意的是，我们并不是在断言 \(\mu \in \left( \overline{X} - 1.96 \frac{\sigma}{\sqrt{n}}, \overline{X} + 1.96 \frac{\sigma}{\sqrt{n}} \right)\) 的概率为 0.95，这主要是因为在如上的断言中并没有涉及到任何 随机变量。我们所断言的是，使用这种方法得到的区间会有 95% 的概率包含 \(\mu\)。换句话说，观测到数据之前，我们可以断言该区间有 0.95 的概率将包含 \(\mu\)；而在观测到数据之后，我们只能断言结果区间确实以 0.95 的置信度包含 \(\mu\)。
习题 7.10 根据以往的经验，在商业孵化场中养殖的三文鱼的重量符合正态分布，其均值会随季节的不同而不同，但其标准差固定为 0.3 磅。如果我们想在 95% 的置信度下，估计当前季节三文鱼的平均重量，并且估计的误差在 \(\pm 0.1\) 磅以内，需要多大的样本量？
解 7.10. 基于样本量 \(n\) 的未知均值 \(\mu\) 的 95% 置信区间估计为：
\(\mu \in \left( \overline{X} - 1.96 \frac{\sigma}{\sqrt{n}}, \overline{X} + 1.96 \frac{\sigma}{\sqrt{n}} \right)\)
因为估计区间中的任何一个估计值都在 \(\overline{X}\) 的 \(1.96(\sigma / \sqrt{n}) = \frac{0.588}{\sqrt{n}}\) 以内，因此我们可以 95% 地确信，\(\overline{X}\) 在 \(\mu\) 的 0.1 以内的前提是：
\(\frac{0.588}{\sqrt{n}} \leq 0.1\)
也就是说 \(\sqrt{n} \geq 5.88\)，即 \(n \geq 34.57\)。也就是说，样本量为 35 或更大就足够了。 \(\blacksquare\)
7.3.1 方差未知时正态分布均值的置信区间
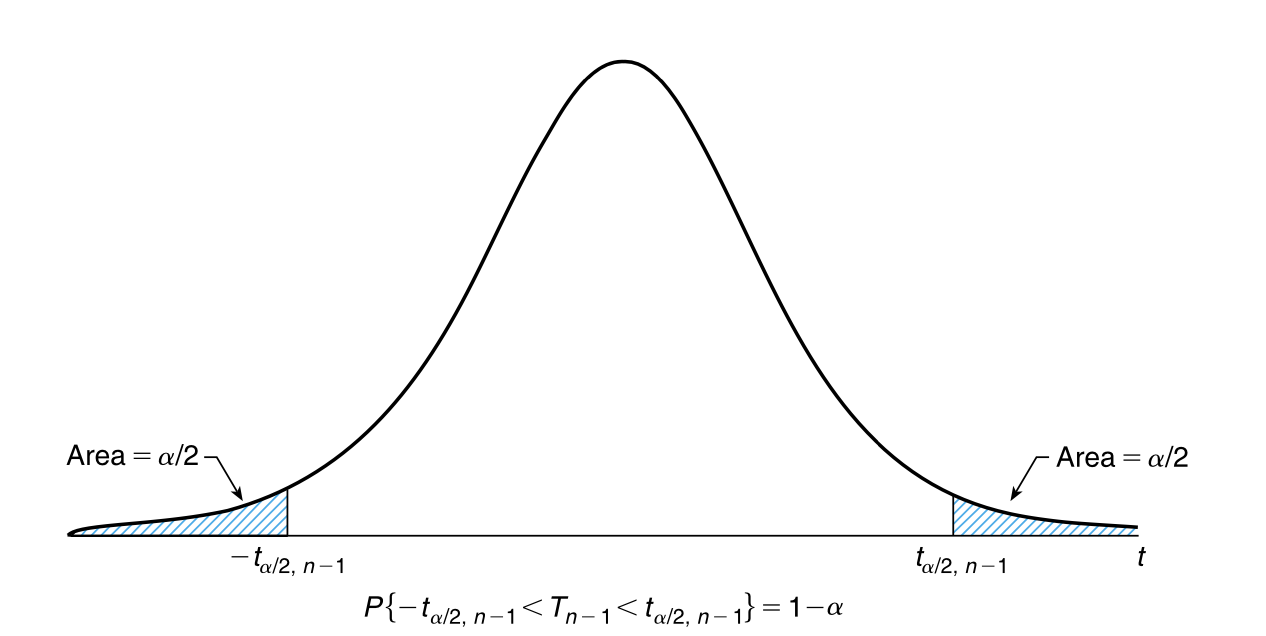
假设 \(X_1, ..., X_n\) 是来自均值 \(\mu\)、方差 \(\sigma^2\) 均未知的正态分布的样本，我们希望计算 \(\mu\) 的 \(100(1-\alpha)\%\) 置信区间估计。当方差 \(\sigma^2\) 未知时，我们不能再认为 \(\sqrt{n} \frac{\overline{X} - \mu}{\sigma}\) 是一个标准正态分布的 随机变量。但是，令 \(S^2 = \sum_{i=1}^{n}(X_i - \overline{X})^2 / (n-1)\) 为样本方差，那么根据 推论 6.1 可知
\(\sqrt{n} \frac{\overline{X} - \mu}{S}\)
符合自由度为 \(n-1\) 的 \(t\) 分布。因此，根据 \(t\) 分布的概率密度函数的对称性（图 7.2），对于任何 \(\alpha \in (0, 1/2)\) ，我们都有
\(P\left\{ -t_{\alpha/2, n-1} < \sqrt{n} \frac{\overline{X} - \mu}{S} < t_{\alpha/2, n-1} \right\} = 1 - \alpha\)
即
\(P\left\{ -t_{\alpha/2, n-1} \frac{S}{\sqrt{n}} < \overline{X} - \mu < t_{\alpha/2, n-1} \frac{S}{\sqrt{n}} \right\} = 1 - \alpha\)
于是，得到
\(P\left\{ \overline{X} - t_{\alpha/2, n-1} \frac{S}{\sqrt{n}} < \mu < \overline{X} + t_{\alpha/2, n-1} \frac{S}{\sqrt{n}} \right\} = 1 - \alpha\)
因此，根据观测到的样本数据 \(\overline{X} = \overline{x}\) 且 \(S = s\) ，我们可以说“ \(\mu\) 的 \(100(1-\alpha)\%\) 置信度区间估计”为：
\(\mu \in \left( \overline{x} - t_{\alpha/2, n-1} \frac{s}{\sqrt{n}}, \overline{x} + t_{\alpha/2, n-1} \frac{s}{\sqrt{n}} \right)\)
习题 7.11 让我们再次考虑 习题 7.7，但现在假设在 A 地传输值为 \(\mu\) 的信号时，在 B 地接收到的值符合均值为 \(\mu\)、方差为 \(\sigma^2\) 的正态分布，但是 \(\sigma^2\) 未知。如 习题 7.7 所示，如果连续发送 9 个信号，B 地接收到的信号值分别为：
5、8.5、12、15、7、9、7.5、6.5、10.5
请计算 \(\mu\) 的 95% 置信区间。
解 7.11. 样本均值 \(\overline{x} = 9\)，样本标准差 \(s^2 = \frac{\sum(x_i - \overline{x})^2}{8} = 9.5\)，即 \(s = 3.082\)。
代码
qt(0.025, df=8, lower.tail=FALSE)[1] 2.306004因为 \(t_{0.025, 8} = 2.306\)，因此，\(\mu\) 的 95% 置信区间为：
\(\bigg(9-2.306 \frac{3.082}{3}, 9+2.306 \frac{3.082}{3}\bigg) = (6.63, 11.37)\)
可见，如上的结果比 Solution 7.7 中得到的区间要大，这里主要有两个原因：
- 最主要的原因是，我们在这里对方差的估计值比 Solution 7.7 中的方差更大。也就是说，在 Solution 7.7 中，我们假设 \(\sigma^2\) 已知并等于 4；而在本例中，我们假设方差是未知的，并且我们的估计值为 9.5。更大的方差导致我们得到了一个更大范围的置信区间。
- 事实上，即使我们估计的 \(\sigma^2\) 依旧是 4，因为方差未知，我们仍然需要利用 \(t\) 分布来估计方差。因为 \(t\) 分布的方差比标准正态分布的方差更大，因此获得的区间范围也会比标准正态分布更宽。例如，如果 \(\overline{x} = 9\) 且 \(s^2 = 4\)，那么我们的置信区间将是：
\((9 - 2.306 \cdot \frac{2}{3}, 9 + 2.306 \cdot \frac{2}{3}) = (7.46, 10.54)\)
这显然比 Solution 7.7 中的 \((7.69, 10.31)\) 的区间更大。\(\blacksquare\)
注意
当 \(\sigma\) 已知时，\(\mu\) 的置信区间基于以下事实：\(\sqrt{n}(\overline{X} - \mu)/\sigma\) 服从标准正态分布。当 \(\sigma\) 未知时，可以利用样本标准差 \(S\) 来估计总体标准差 \(\sigma\)，然后利用以下事实——\(\sqrt{n}(\overline{X} - \mu)/S\) 服从自由度为 \(n - 1\) 的 \(t\) 分布——来计算 \(\mu\) 的置信区间估计。
当总体方差未知时，\(\mu\) 的 \(100(1-2\alpha)\%\) 置信区间的长度并不总是比方差已知时的更长。当 \(\sigma\) 已知时，置信区间估计的长度是 \(2z_{\alpha}\frac{\sigma}{\sqrt{n}}\)；而当 \(\sigma\) 未知时，其长度是 \(2t_{\alpha, n-1}\frac{S}{\sqrt{n}}\)。并且，确实存在如下的可能性：样本标准差 \(S\) 远小于总体标准差 \(\sigma\)。但是，我们依然可以证明，当总体方差未知时，\(\mu\) 的置信区间的平均长度会更长。也就是说，可以证明：
\(t_{\alpha, n-1} E[S] \geq z_{\alpha}\sigma\)
我们会在 章节 14 中计算 \(E[S]\)，例如：
\(E[S] = \begin{cases}0.94\sigma, \quad n = 5 & \\0.97\sigma, \quad n = 9 &\end{cases}\)
因为 \(z_{0.025} = 1.96\)， \(t_{0.025,4} = 2.78\)， \(t_{0.025,8} = 2.31\)，所以样本量为 5 时，当方差已知时，95% 的置信区间长度是 \(2 \times 1.96 \times \frac{\sigma}{5} = 1.75 \sigma\)；而当方差未知时，其预期长度是 \(2 \times 2.78 \times \frac{0.94\sigma}{\sqrt{5}} = 2.34\sigma\)。因此可以看出，当方差未知时，置信区间的长度增加了 33.7%。如果样本量为 9，则方差已知和方差未知时的 95% 置信区间长度分别为 \(1.31\sigma\) 和 \(1.49\sigma\)，置信区间长度增加了 13.7%。
当总体方差未知时，我们可以得到 \(\mu\) 的单边上置信区间估计为：
\(P\bigg\{\sqrt{n}\frac{\overline{X} - \mu}{S} \lt t_{\alpha, n-1}\bigg\} = 1 - \alpha\)，即
\(P\bigg\{\overline{X} - \mu \lt \frac{S}{\sqrt{n}}t_{\alpha, n-1} \bigg\} = 1 - \alpha\)，即
\(P\bigg\{\mu \gt \overline{X} - \frac{S}{\sqrt{n}}t_{\alpha, n-1} \bigg\} = 1 - \alpha\)
因此，对于观察到的样本数据而言，\(\overline{X} = \overline{x}\)，\(S=s\)，我们有“有 \(100(1-\alpha)\%\) 的信心” 可以断言：
\(\mu \in \bigg(\overline{x} - \frac{S}{\sqrt{n}}t_{\alpha, n-1}, \infty\bigg)\)
同理，我们可以得到总体方差未知时，\(\mu\) 的单边下置信区间估计为：
\(\mu \in \bigg(-\infty, \overline{x} + \frac{S}{\sqrt{n}}t_{\alpha, n-1}\bigg)\)
我们可以使用 R 来获得置信区间。要得到 \(x_1, ..., x_n\) 的 \(100(1-\alpha)\%\) 置信区间，我们可以在 R 中执行如下操作：
d <- c(x1,...,xn)
l <- mean(d) − qt(1−α/2, n−1) * sqrt(var(d) / n)
u <- mean(d) + qt(1−α/2, n−1) * sqrt(var(d) / n)
c(l, u)例如，在正态分布的总体方差未知时，我们要计算该正态分布的均值的 99% 置信区间，其中数据样本为：
5, 9, 12, 8.6, 7.2, 13, 9.5
d <- c(5, 9, 12, 8.6, 7.2, 13, 9.5)
l <- mean(d) - qt(.995, 6) * sqrt(var(d) / 7)
u <- mean(d) + qt(.995, 6) * sqrt(var(d) / 7)
c(l, u)代码
d <- c(5, 9, 12, 8.6, 7.2, 13, 9.5)
l <- mean(d) - qt(.995, 6) * sqrt(var(d) / 7)
u <- mean(d) + qt(.995, 6) * sqrt(var(d) / 7)
c(l, u)[1] 5.373463 12.997965习题 7.12 从某健身俱乐部的成员中随机选择了 15 名成员并得到了如下的静息心率数据：
54、63、58、72、49、92、70、73、69、104、48、66、80、64、77
确定该健身俱乐部成员的平均静息心率的 95% 置信区间和 95% 上置信区间。
解 7.12. 双边 95% 置信区间为：\((60.86694, 77.66640)\)
代码
d <- c(54, 63, 58, 72, 49, 92, 70, 73, 69, 104, 48, 66, 80, 64, 77)
l <- mean(d) - qt(.975, 14) * sqrt(var(d) / 15)
u <- mean(d) + qt(.975, 14) * sqrt(var(d) / 15)
c(l, u)[1] 60.86694 77.66640单边 95% 上置信区间为：\((62.36876, \infty)\)
代码
d <- c(54, 63, 58, 72, 49, 92, 70, 73, 69, 104, 48, 66, 80, 64, 77)
ub <- mean(d) - qt(.95, 14) * sqrt(var(d) / 15)
ub[1] 62.36876\(\blacksquare\)
我们假定总体分布是正态分布，然后推导出总体均值 \(\mu\) 的 \(100(1-\alpha) \%\) 置信区间。然而，即使总体不是正态分布，根据中心极限定理（定理 6.1），如果样本量足够大，那么 \(\sqrt{n}(\overline{X} - \mu)/\sigma\) 将近似服从正态分布，并且 \(\sqrt{n}(\overline{X} - \mu)/S\) 将近似服从 \(t\) 分布，因此 \(\mu\) 的区间估计仍将近似于 \(100(1-\alpha) \%\) 置信区间。
例 7.2 统计模拟法（simulation）提供了一种强大的方法以计算一维积分和多维积分。例如，设 \(f\) 是一个 \(r\) 维向量 \((y_1, y_2, \ldots, y_r)\) 的函数，并且假设我们想要对如下的 进行估计：
\(\theta = \int_{0}^{1} \int_{0}^{1} \cdots \int_{0}^{1} f(y_1, y_2, \ldots, y_r) dy_1 dy_2 \ldots dy_r\)
如果 \(U_1, U_2, \ldots, U_r\) 是 \((0, 1)\) 上的、相互独立的均匀分布随机变量，那么
\(\theta = E[f(U_1, U_2, \ldots, U_r)]\)
现在，我们可以（通过所谓的伪随机数）在计算机上近似模拟独立 \((0, 1)\) 均匀分布随机变量的值。如果我们生成一个 \(r\) 维向量，并在该向量上计算 \(f\)，那么由此得到的值——\(X_1\)——将是均值为 \(\theta\) 的随机变量。如果我们重复这个过程，那么我们得到另一个值——\(X_2\)——将与 \(X_1\) 的分布相同。继续下去，我们可以生成一个序列 \(X_1, X_2, \ldots, X_n\)，他们是独立、同分布的随机变量，并且均值为 \(\theta\)。然后我们就可以利用 \(X_1, X_2, \ldots, X_n\) 的观察值来估计 \(\theta\)。我们将这种近似积分的方法称为 蒙特卡罗模拟（Monte Carlo simulation）。
例如，假设我们想要估计一维积分：
\(\theta = \int_{0}^{1} \sqrt{1 - y^2} dy = E[\sqrt{1 - U^2}]\)
其中，\(U\) 是一个 \((0, 1)\) 均匀随机变量。
为此，设 \(U_1, \ldots, U_{100}\) 为 \((0, 1)\) 上的独立均匀随机变量，并设
\(X_i = \sqrt{1 - U_i^2}, \quad i = 1, \ldots, 100\)
通过这种方式，我们生成了一个均值为 \(\theta\) 的 100 个随机变量的样本。假设计算机生成的 \(U_1, \ldots, U_{100}\) 的随机值所得到的样本 \(X_1, \ldots, X_{100}\) 的样本均值为 0.786、样本标准差为 0.03。
因为 \(t_{0.025, 99} = 1.985\)，因此 \(\theta\) 的 95% 置信区间为：
\(0.786 \pm 1.985 \cdot (0.003)\)
因此，我们有 95% 的信心断言，\(\theta\)（实际为 \(\frac{\pi}{4}\)） 位于区间 \((0.780, 0.792)\) 中。\(\blacksquare\)
7.3.2 预测区间
假设 \(X_1, \ldots, X_n, X_{n+1}\) 是来自均值 \(\mu\) 方差 \(\sigma\) 均未知的正态分布的样本。进一步假设 \(X_1, \ldots, X_n\) 的值是已知的，并且我们希望用它们来预测 \(X_{n+1}\) 的值。
首先，如果均值 \(\mu\) 是已知的，那么 \(\mu\) 就是 \(X_{n+1}\) 的天然预测器。但是由于 \(\mu\) 未知，因此在观察到 \(X_1, \ldots, X_n\) 后，使用这些观测值的平均值作为 \(X_{n+1}\) 的预测值是合理的。也就是说，我们应该使用 \(\overline{X}_n = \sum_{i=1}^n X_i / n\) 作为 \(X_{n+1}\) 的预测值。
现在假设我们想要确定一个区间，在这个区间内，以某种置信度预测 \(X_{n+1}\) 将位于该区间中。为了获得这样的预测区间，注意到 \(\overline{X}_n\) 是具有均值 \(\mu\) 和方差 \(\sigma^2 / n\) 的正态分布，并且它与 \(X_{n+1}\)（均值为 \(\mu\)、方差为 \(\sigma^2\)）是独立的。由此可以得出 \(X_{n+1} - \overline{X}_n\) 的均值为 0、方差为 \(\sigma^2 / n + \sigma^2\)。因此，
\(\frac{X_{n+1} - \overline{X}_n}{\sigma \sqrt{1 + 1/n}}\)
服从标准正态分布。
由于 \(\frac{X_{n+1} - \overline{X}_n}{\sigma \sqrt{1 + 1/n}}\) 与 \(S_n^2 = \sum_{i=1}^n (X_i - \overline{X}_n)^2 / (n - 1)\) 独立，从而根据 推论 6.1 可知，将 \(\sigma\) 替换为其估计量 \(S_n\) 后的表达式是自由度为 \(n - 1\) 的 \(t\) 分布，即，
\(\frac{X_{n+1} - \overline{X}_n}{S_n \sqrt{1 + 1/n}}\)
是自由度为 \(n - 1\) 的 \(t\) 分布随机变量。因此，对于任何 \(\alpha \in (0, 1/2)\)，
\(P \bigg\{ -t_{\alpha/2, n-1} < \frac{X_{n+1} - \overline{X}_n}{S_n \sqrt{1 + 1/n}} < t_{\alpha/2, n-1} \bigg\} = 1 - \alpha\)
即
\(P \bigg\{ \overline{X}_n - t_{\alpha/2, n-1} S_n \sqrt{1 + 1/n} < X_{n+1} < \overline{X}_n + t_{\alpha/2, n-1} S_n \sqrt{1 + 1/n} \bigg\}\)
因此，如果 \(\overline{X}_n\) 和 \(S_n\) 的样本观察值分别是 \(\overline{x}_n\) 和 \(s_n\)，那么我们可以在 \(100(1 - \alpha) \%\) 的置信度下预测 \(X_{n+1}\) 将位于 \(\overline{x}_n - t_{\alpha/2, n-1} s_n \sqrt{1 + 1/n}\) 和 \(\overline{x}_n + t_{\alpha/2, n-1} s_n \sqrt{1 + 1/n}\) 之间。也就是说，在 \(100(1 - \alpha) \%\) 的置信度下，我们可以预测
\[ X_{n+1} \in \left( \overline{x}_n - t_{\alpha/2, n-1} s_n \sqrt{1 + 1/n}, \overline{x}_n + t_{\alpha/2, n-1} s_n \sqrt{1 + 1/n} \right) \]
习题 7.13 以下数据是过去 7 天的步数：
6822, 5333, 7420, 7432, 6252, 7005, 6752
假设每天的步数可以认为服从正态分布，给出一个预测区间，使得在 95% 的置信度下，明天的步数将位于该预测区间。
解 7.13. 计算这 7 个数据值的样本均值和样本方差： \(\overline{X}_7 = 6716.57 , \quad S_7 = 733.97\)
因为 \(t_{0.025, 6} = 2.447\)，并且 \(2.4447 \cdot 733.97 \sqrt{1 + 1/7} = 1920.03\)，我们可以在 95% 的置信度下预测明天的步数将在 6716.57 - 1920.03 和 6716.57 + 1920.03 之间。也就是说，在 95% 的置信度下，\(X_8\) 将位于区间 (4796.54, 8636.60) 内。 \(\blacksquare\)
7.3.3 正态分布方差的置信区间
如果 \(X_1, \ldots, X_n\) 是来自均值 \(\mu\) 和方差 \(\sigma^2\) 均未知的正态分布的样本，那么我们可以根据以下事实（定理 6.2）构造 \(\sigma^2\) 的置信区间：
\((n-1)\frac{S^2}{\sigma^2} \sim \chi^2_{n-1}\)
因此，
\(P \left\{ \chi^2_{1-\alpha/2, n-1} \leq (n-1)\frac{S^2}{\sigma^2} \leq \chi^2_{\alpha/2, n-1} \right\} = 1-\alpha\)
即，
\(P \left\{ \frac{(n-1)S^2}{\chi^2_{\alpha/2, n-1}} \leq \sigma^2 \leq \frac{(n-1)S^2}{\chi^2_{1-\alpha/2, n-1}} \right\} = 1-\alpha\)
因此，当 \(S^2 = s^2\) 时，\(\sigma^2\) 的 \(100(1 - \alpha) \%\) 置信区间为：
\(\left( \frac{(n - 1)s^2}{\chi^2_{\alpha/2, n-1}}, \frac{(n - 1)s^2}{\chi^2_{1-\alpha/2, n-1}} \right)\)
习题 7.14 我们希望一个标准化流水线生产的垫片的厚度差异很小。假设我们选取了 10 个这样的垫片并测量其厚度。如果这些垫片的厚度（单位：英寸）如下所示：
0.123 0.133 0.124 0.125 0.126 0.128 0.120 0.124 0.130 0.126
那么，该流水线生产的垫片厚度的标准差的 90% 置信区间是多少？
解 7.14. 使用 R，我们有：
>d = c(0.123, 0.124, 0.126, 0.120, 0.130, 0.133, 0.125, 0.128, 0.124, 0.126)
>l = 9 * var(d) / qchisq(0.95, 9)
>u = 9 * var(d) / qchisq(0.05, 9)
>c(l, u)代码
d = c(0.123, 0.124, 0.126, 0.120, 0.130, 0.133, 0.125, 0.128, 0.124, 0.126)
l = 9 * var(d) / qchisq(0.95, 9)
u = 9 * var(d) / qchisq(0.05, 9)
c(l, u)[1] 7.264032e-06 3.696115e-05由此可见，\(\sigma^2\) 的 90% 的置信区间为：
\(\sigma^2 \in (7.2640 \times 10^{-6}, 36.9612 \times 10^{-6})\)
所以：
\(\sigma \in (0.00269, 0.00608)\)
类似的，可以得到 \(\sigma^2\) 的单边置信区间。表 7.1 对本节的内容进行了总结。
| 假设 | 参数 | 置信区间 | 单边下置信区间 | 单边上置信区间 |
|---|---|---|---|---|
| \(\sigma^2\) 已知 | \(\mu\) | \(\overline{X} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\) | \((-\infty, \overline{X} + z_{\alpha} \frac{\sigma}{\sqrt{n}})\) | \((\overline{X} - z_{\alpha} \frac{\sigma}{\sqrt{n}}, \infty)\) |
| \(\sigma^2\) 未知 | \(\mu\) | \(\overline{X} \pm t_{\alpha/2, n-1} \frac{S}{\sqrt{n}}\) | \((-\infty, \overline{X} + t_{\alpha, n-1} \frac{S}{\sqrt{n}})\) | \((\overline{X} - t_{\alpha, n-1} \frac{S}{\sqrt{n}}, \infty)\) |
| \(\mu\) 未知 | \(\sigma^2\) | \(\left( \frac{(n - 1) S^2}{\chi^2_{\alpha/2, n-1}}, \frac{(n - 1) S^2}{\chi^2_{1-\alpha/2, n-1}} \right)\) | \(\left(0, \frac{(n - 1) S^2}{\chi^2_{1 - \alpha, n-1}}\right)\) | \(\left(\frac{(n - 1) S^2}{\chi^2_{\alpha, n-1}}, \infty\right)\) |
7.4 估计两个正态分布总体的均值差异
令 \(X_1, X_2, \dots, X_n\) 是来自均值为 \(\mu_1\)、方差为 \(\sigma_1^2\) 的正态分布的总体的一个样本，样本大小为 \(n\)；\(Y_1, \dots, Y_m\) 是来自均值为 \(\mu_2\)、方差为 \(\sigma_2^2\) 的另一个正态分布总体的一个样本，样本大小为 \(m\)。假设这两个样本之间彼此相互独立。此时，我们感兴趣的是：如何估计 \(\mu_1 - \mu_2\)？
因为 \(\mu_1\) 和 \(\mu_2\) 的最大似然估计分别是：\(\overline{X} = \sum_{i=1}^n X_i / n\)、\(\overline{Y} = \sum_{i=1}^m Y_i / m\)，所以直觉而言（并且可以证明）\(\mu_1 - \mu_2\) 的最大似然估计是 \(\overline{X} - \overline{Y}\)。
为了得到置信区间估计，我们需要计算 \(\overline{X} - \overline{Y}\) 的分布。由于
\(\begin{align} \overline{X} &\sim \mathcal{N}\left(\mu_1, \frac{\sigma_1^2}{n}\right) \\ \overline{Y} & \sim \mathcal{N}\left(\mu_2, \frac{\sigma_2^2}{m}\right) \end{align}\)
根据独立正态分布随机变量的和也是正态分布的性质，有：
\(\overline{X} - \overline{Y} \sim \mathcal{N}\left(\mu_1 - \mu_2, \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}\right)\)
因此，假设 \(\sigma_1^2\) 和 \(\sigma_2^2\) 是已知的，我们有：
\[ \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) \tag{7.5}\]
因此，
\(P\left\{-z_{\alpha/2} < \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha/2}\right\} = 1 - \alpha\)
即：
\(P\left\{\overline{X} - \overline{Y} - z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}} < \mu_1 - \mu_2 < \overline{X} - \overline{Y} + z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\right\} = 1 - \alpha\)
因此，如果获得了样本的观察数据，则 \(\overline{X}\) 和 \(\overline{Y}\) 分别等于 \(\overline{x}\) 和 \(\overline{y}\)，那么 \(\mu_1 - \mu_2\) 的 \(100(1-\alpha)\%\) 双边置信区间估计为：
\[ \mu_1 - \mu_2 \in \left(\overline{x} - \overline{y} - z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}, \, \overline{x} - \overline{y} + z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\right) \tag{7.6}\]
类似的，可以得到 \(\mu_1 - \mu_2\) 的 \(100(1-\alpha)\%\) 的单边置信区间：
\[ \mu_1 - \mu_2 \in \left(-\infty, \, \overline{x} - \overline{y} + z_{\alpha}\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\right) \tag{7.7}\]
式 7.7 的证明我们留给读者来进行验证。
习题 7.15 我们对两种不同类型的电缆绝缘材料进行了测试，以确定故障发生时的电压水平。在实验室的实验中，在电压不断增加的情况下，两种类型的电缆绝缘材料在如下的电压下发生了故障：
| Type A | Type B |
|---|---|
| 36 | 52 |
| 44 | 64 |
| 41 | 38 |
| 53 | 68 |
| 38 | 66 |
| 36 | 52 |
| 34 | 60 |
| 54 | 44 |
| 52 | 48 |
| 37 | 46 |
| 51 | 70 |
| 44 | 62 |
| 35 | |
| 44 |
假设已知绝缘材料 A 所能承受的电压服从均值为 \(\mu_A\)（未知）、方差为 \(\sigma_A^2 = 40\) 的正态分布；而绝缘材料 B 服从均值为 \(\mu_B\)（未知）、方差为 \(\sigma_B^2 = 100\) 的正态分布。
- 确定 \(\mu_B - \mu_A\) 的 95% 置信区间。
- 确定我们可以以 95% 的置信度断言比 \(\mu_B - \mu_A\) 小的最大值。
解 7.15.
x <- c(52, 64, 38, 68, 66, 52, 60, 44, 48, 46, 70, 62)
y <- c(36, 44, 41, 53, 38, 36, 34, 54, 52, 37, 51, 44, 35, 44)
l <- mean(x) - mean(y) - qnorm(.975) * sqrt(40 / 14 + 100 / 12)
u <- mean(x) - mean(y) + qnorm(.975) * sqrt(40 / 14 + 100 / 12)
c(l,u)[1] 6.491114 19.604124因此，我们有 95% 的信心可以断言 \(\mu_B - \mu_A \in (6.491114, 19.604124)\)。为了获得单边上置信区间，我们可以采用如下的 R 代码：
x <- c(52, 64, 38, 68, 66, 52, 60, 44, 48, 46, 70, 62)
y <- c(36, 44, 41, 53, 38, 36, 34, 54, 52, 37, 51, 44, 35, 44)
u <- mean(x) - mean(y) - qnorm(.95) * sqrt(40 / 14 + 100 / 12)
u[1] 7.545227因此，我们有 95% 的信心认为 \(\mu_B - \mu_A \ge 7.545227\)。\(\blacksquare\)
7.4.1 总体方差未知时 \(\mu_1 - \mu_2\) 的区间估计
现在，我们希望再次对 \(\mu_1 - \mu_2\) 进行区间估计，但这次估计时的总体方差 \(\sigma_1^2\) 和 \(\sigma_2^2\) 均是未知的。在这种情况下，最直接的做法就是用 样本方差 来替换公式 式 7.5 中的总体方差 \(\sigma_1^2\) 和 \(\sigma_2^2\)：
\(\begin{align} S_1^2 &= \frac{\sum_{i=1}^n (X_i - \overline{X})^2}{n - 1} \\ S_2^2 &= \frac{\sum_{i=1}^m (Y_i - \overline{Y})^2}{m - 1} \end{align}\)
也就是说，此时的区间估计很自然地变为如下的形式：
\[ \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{S_1^2/n + S_2^2/m}} \tag{7.8}\]
然而，为了利用 式 7.8 计算置信区间，我们需要知道 式 7.8 的分布，并且该分布不能依赖于任何未知参数 \(\sigma_1^2\) 和 \(\sigma_2^2\)。不幸的是，这个分布既复杂又确实依赖于未知参数 \(\sigma_1^2\) 和 \(\sigma_2^2\)。事实上，只有在特殊情况下，即 \(\sigma_1^2 = \sigma_2^2\) 时，我们才能获得 \(\mu_1 - \mu_2\) 的区间估计。因此，虽然总体方差未知，但我们可以假设总体方差是一致的，并令 \(\sigma^2\) 表示 \(\sigma_1^2\) 和 \(\sigma_2^2\) 的值。由 定理 6.2 得到：
\(\begin{align} (n - 1)\frac{S_1^2}{\sigma^2} & \sim \chi^2_{n-1} \\ (m - 1)\frac{S_2^2}{\sigma^2} & \sim \chi^2_{m-1} \end{align}\)
此外，由于样本是独立的，因此这两个卡方随机变量也是独立的。由卡方随机变量的可加性，独立卡方随机变量之和也是卡方分布，其自由度等于各卡方随机变量的自由度之和，因此有：
\[ (n - 1)\frac{S_1^2}{\sigma^2} + (m - 1)\frac{S_2^2}{\sigma^2} \sim \chi^2_{n+m-2} \tag{7.9}\]
同时，由于
\(\overline{X} - \overline{Y} \sim \mathcal{N}\left(\mu_1 - \mu_2, \frac{\sigma^2}{n} + \frac{\sigma^2}{m}\right)\)
我们可以得到：
\[ \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\sigma^2/n + \sigma^2/m}} \sim \mathcal{N}(0, 1) \tag{7.10}\]
现在，根据 定理 6.2 中的基本结果，在正态分布抽样中，\(\overline{X}\) 和 \(S^2\) 是独立的，所以 \(X_1, S_1^2, X_2, S_2^2\) 是独立的随机变量。因此，如果令：
\(S_p^2 = \frac{(n-1)S_1^2 + (m-1)S_2^2}{n+m-2}\)
使用 \(t\) 随机变量的定义（小节 5.8.2，\(t\) 随机变量为两个独立随机变量的比值，其中分子为标准正态分布，分母为一个卡方随机变量除以其自由度的平方根），根据 式 7.9 和 式 7.10 可以得到：
\(\frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\sigma^2 (1/n + 1/m)}} \div \sqrt{\frac{S_p^2}{\sigma^2}} = \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{S_p^2 (1/n + 1/m)}}\)
是自由度为 \(n + m - 2\) 的 \(t-\text{分布}\) 随机变量。因此：
\(P\left\{ -t_{\alpha/2, n+m-2} \leq \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{S_p \sqrt{1/n + 1/m}} \leq t_{\alpha/2, n+m-2} \right\} = 1 - \alpha\)
因此，当观察到样本数据后，令 \(\overline{X} = \overline{x}\)、\(\overline{Y} = \overline{y}\)、\(S_p = s_p\)，我们得到 \(\mu_1 - \mu_2\) 的 \(100(1-\alpha)\%\) 的置信区间：
\[ \left(\overline{x} - \overline{y} - t_{\alpha/2, n+m-2} s_p \sqrt{1/n + 1/m}, \quad \overline{x} - \overline{y} + t_{\alpha/2, n+m-2} s_p \sqrt{1/n + 1/m}\right) \tag{7.11}\]
类似地，我们可以得到方差未知时 \(\mu_1 - \mu_2\) 的单边置信区间。
习题 7.16 对于 习题 7.15 中的数据，如果两个样本的总体方差均未知、但是方差是相等的，计算 \(\mu_B - \mu_A\) 的 95% 的双边置信区间？
解 7.16.
x <- c(52, 64, 38, 68, 66, 52, 60, 44, 48, 46, 70, 62)
y <- c(36, 44, 41, 53, 38, 36, 34, 54, 52, 37, 51, 44, 35, 44)
sp <- sqrt((11 * var(x) + 13 * var(y)) / 24)
l <- mean(x) - mean(y) - qt(0.975, 24) * sp * sqrt(1 / 12 + 1 / 14)
u <- mean(x) - mean(y) + qt(0.975, 24) * sp * sqrt(1 / 12 + 1 / 14)
c(l,u)[1] 5.830952 20.264286\(\blacksquare\)
备注
由 式 7.11 给出的置信区间是在假设总体方差相等的条件下的结果；假设抽样的总体的方差都是 \(\sigma^2\)，则
\(\frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\sigma^2/n + \sigma^2/m}} = \frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sigma\sqrt{1/n + 1/m}}\)
服从标准正态分布。
然而，由于 \(\sigma^2\) 是未知的，因此不能直接使用上式来计算置信区间。为了计算置信区间，必须首先估计 \(\sigma^2\)。同时，请注意，两个样本方差都是 \(\sigma^2\) 的估计量。此外，由于 \(S_1^2\) 的自由度为 \(n - 1\)，\(S_2^2\) 的自由度为 \(m - 1\)，所以取这两个样本方差的估计量的加权平均值（权重与自由度成正比）作为 \(\sigma^2\) 的估计量是合理的。也就是说，\(\sigma^2\) 的估计量是 池化估计量（the pooled estimator）：
\(S_p^2 = \frac{(n - 1)S_1^2 + (m - 1)S_2^2}{n + m - 2}\)
于是基于以下统计量计算置信区间：
\(\frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{S_p^2\left(1/n + 1/m\right)}}\)
根据之前的分析，如上的统计量服从自由度为 \(n + m - 2\) 的 \(t- \text{分布}\)。
表 7.2 对本节的相关结论进行了总结。
| \(\begin{align} & X_1, ..., X_n \sim \mathcal{N}(\mu_1, \sigma_1^2) \\ & Y_1, ..., Y_n \sim \mathcal{N}(\mu_2, \sigma_2^2) \\ & \overline{X} = \sum_{i=1}^{n}{X_i} / n, \quad S_1^2 = \sum_{i=1}^{n}{(X_i - \overline{X})^2} / (n-1) \\ & \overline{Y} = \sum_{i=1}^{m}{Y_i} / n, \quad S_2^2 = \sum_{i=1}^{m}{(Y_i - \overline{Y})^2} / (m-1)\end{align}\) |
| Assumption | Confidence Interval |
|---|---|
| \(\sigma_1, \sigma_2\) 已知 | \(\overline{X} - \overline{Y} \pm z_{\alpha/2} \sqrt{\sigma_1^2/n + \sigma_2^2/m}\) |
| \(\sigma_1, \sigma_2\) 未知但相等 | \(\overline{X} - \overline{Y} \pm t_{\alpha/2, n+m-2} \sqrt{\left(\frac{1}{n} + \frac{1}{m}\right) \frac{(n-1)S_1^2 + (m-1)S_2^2}{n+m-2}}\) |
| Assumption | Lower Confidence Interval |
|---|---|
| \(\sigma_1, \sigma_2\) 已知 | \((-\infty, \overline{X} - \overline{Y} + z_{\alpha} \sqrt{\sigma_1^2/n + \sigma_2^2/m})\) |
| \(\sigma_1, \sigma_2\) 未知但相等 | \(\left(-\infty, \overline{X} - \overline{Y} + t_{\alpha, n+m-2} \sqrt{\left(\frac{1}{n} + \frac{1}{m}\right) \frac{(n-1)S_1^2 + (m-1)S_2^2}{n+m-2}}\right)\) |
注意：\(\mu_1 - \mu_2\) 的单边上置信区间可以通过 \(\mu_2 - \mu_1\) 的单边下执行区间得到
7.5 伯努利随机变量均值的近似置信区间
考虑某个物品的一个总体，总体中每个物品达到某些标准的概率都是未知概率 \(p\)，并且物品之间的达标率是相互独立的。如果我们从总体中抽取 \(n\) 个物品进行测试，以确定这些物品是否达到标准，我们如何利用抽检所得到的数据来计算 \(p\) 的置信区间？
如果我们令 \(X\) 表示抽取的 \(n\) 个物品中符合标准的物品数量，那么 \(X\) 是参数为 \((n, p)\) 的二项随机变量。因此，当 \(n\) 较大时，根据二项分布会近似为正态分布的特性（小节 6.3），\(X\) 近似服从均值为 \(np\)、方差为 \(np(1-p)\) 的正态分布。因此，
\[ \frac{X - np}{\sqrt{np(1-p)}} \approx \mathcal{N}(0, 1) \tag{7.12}\]
其中 \(\approx\) 表示“近似服从”。因此，对于任何 \(\alpha \in (0, 1)\)，我们有：
\(P\left\{-z_{\alpha/2} < \frac{X - np}{\sqrt{np(1-p)}} < z_{\alpha/2}\right\} \approx 1 - \alpha\)
因此，如果对于实验数据 \(X = x\) 而言，\(p\) 的近似 \(100(1-\alpha)\%\) 置信区为：
\[ \left\{p : -z_{\alpha/2} < \frac{x - np}{\sqrt{np(1-p)}} < z_{\alpha/2}\right\} \tag{7.13}\]
然而，式 7.13 的区域并非区间。令 \(\hat{p} = X/n\) 表示符合标准的物品所占的比例，以便得到 \(p\) 的置信区间。根据 习题 7.1 可知，\(\hat{p}\) 是 \(p\) 的最大似然估计，因此 \(\hat{p}\) 应该近似等于 \(p\)。因此，\(\sqrt{n\hat{p}(1-\hat{p})}\) 将近似等于 \(\sqrt{np(1-p)}\)，因此由 式 7.12 可以得到：
\(\frac{X - np}{\sqrt{n\hat{p}(1-\hat{p})}} \approx \mathcal{N}(0, 1)\)
因此，对于任何 \(\alpha \in (0, 1)\)，我们有：
\(P\left\{-z_{\alpha/2} < \frac{X - np}{\sqrt{n\hat{p}(1-\hat{p})}} < z_{\alpha/2}\right\} \approx 1 - \alpha\)
即，
\(P\{-z_{\alpha/2}\sqrt{n\hat{p}(1-\hat{p})} < np - X < z_{\alpha/2}\sqrt{n\hat{p}(1-\hat{p})}\} \approx 1 - \alpha\)
将上述不等式两边都除以 \(n\)，并根据 \(\hat{p} = X/n\)，有：
\[ P\left\{\hat{p} - z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p} + z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right\} \approx 1 - \alpha \tag{7.14}\]
式 7.14 给出了 \(p\) 的 \(100(1-\alpha)\%\) 的近似置信区间。
例 7.3 从一批晶体管中随机抽取 100 个样本，并测试这 100 个样本是否符合当前标准。如果其中有 80 个晶体管符合标准，那么符合标准的所有晶体管的比例 \(p\) 的近似 95% 置信区间为：
\((0.8 - 1.96 \sqrt{\frac{0.8(0.2)}{100}}, \, 0.8 + 1.96 \sqrt{\frac{0.8(0.2)}{100}}) = (0.7216, \, 0.8784)\)
也就是说，在 95% 的置信度的情况下，符合标准的晶体管的比例在 72.16% 到 87.84% 之间。
习题 7.17 2013 年 8 月，《纽约时报》报道了最近的一项民意调查，结果显示 52% 的人（误差范围为 \(\pm 4\%\)）对奥巴马总统的工作表现呈肯定态度。这意味着什么？我们能推断出有多少人参与了调查吗？
解 7.17. 新闻媒体通常会使用 95% 置信区间。由于 \(z_{0.025} = 1.96\)，令 \(p\) 代表肯定奥巴马总统工作表现的人的比例，那么关于 \(p\) 的 95% 置信区间可以表示为：
\(\hat{p} \pm 1.96 \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} = 0.52 \pm 1.96 \sqrt{\frac{0.52 \times 0.48}{n}}\)
其中，\(n\) 是样本的大小。由于“误差范围”是 \(\pm 4\%\)，由此可以推导出：
\(1.96 \sqrt{\frac{0.52 \times 0.48}{n}} = 0.04\)
即：
\(n = \frac{(1.96)^2 \times 0.52 \times 0.48}{(0.04)^2} = 599.29\)
也就是说，大约有 599 人参与了调查，其中 52% 的人对奥巴马总统的工作表现持肯定态度。 \(\blacksquare\)
我们经常希望为 \(p\) 指定一个近似的 \(100(1 - \alpha)\%\) 的置信区间，并且该置信区间的长度不能超过某个给定的值（\(b\)）。获得这样的、有大小限定的置信区间的问题在于确定合适的样本量 \(n\)。从样本大小为 \(n\) 的样本中得到的 \(p\) 的近似 \(100(1 - \alpha)\%\) 的置信区间的长度为：
\(2z_{\alpha/2} \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}\)
该值近似等于 \(2z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\)。不幸的是，因为 \(p\) 是未知的，因此我们不能简单地令 \(2z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} = b\)，然后再确定所需的样本量 \(n\)。然而，我们可以先进行一个初步的抽样，以获得 \(p\) 的粗略估计，然后利用该估计来确定 \(n\)。
也就是说，我们使用初步抽样样本中的比例 \(p^*\) 作为 \(p\) 的初步估计；然后通过求解下列方程确定总样本量 \(n\)：
\(2z_{\alpha/2} \sqrt{\frac{p^*(1 - p^*)}{n}} = b\)
对上式两边平方得到：
\((2z_{\alpha/2})^2 \frac{p^*(1 - p^*)}{n} = b^2\)
即：
\(n = \frac{(2z_{\alpha/2})^2 p^*(1 - p^*)}{b^2}\)
也就是说，如果最初抽取了 \(k\) 个样本以获得 \(p\) 的初步估计，那么还应再抽取 \(n - k\) 个样本。
例 7.4 某芯片制造商生产的每个芯片的达标率为某个未知概率 \(p\)（假设芯片之间的达标率是相互独立的）。已经抽取了 30 个芯片的初步样本以便获得区间长度为 0.05 的 \(p\) 的近似 99% 置信区间。在抽取的 30 个芯片中，如果有 26 个芯片符合标准（达标），那么 \(p\) 的初步估计为 \(26/30\)。使用该值，得到长度为 0.05 的 99% 置信区间所需的样本量为：
\(n = \frac{4(z_{0.005})^2 \cdot \frac{26}{30} \left(1 - \frac{26}{30}\right)}{(0.05)^2} = \frac{4(2.58)^2 \cdot \frac{26}{30} \cdot \frac{4}{30}}{(0.05)^2} = 1231\)
因此，我们现在应该再抽取 1201 个芯片，并且如果其中有 1040 个芯片是符合标准的，那么 \(p\) 的最终 99% 置信区间为：
\(\left(\frac{1066}{1231} - \sqrt{\frac{1066}{1231} \left(1 - \frac{1066}{1231}\right)} \cdot \frac{z_{0.005}}{\sqrt{1231}}, \, \frac{1066}{1231} + \sqrt{\frac{1066}{1231} \left(1 - \frac{1066}{1231}\right)} \cdot \frac{z_{0.005}}{\sqrt{1231}}\right)\)
即：
\(p \in (0.84091, 0.89101)\) \(\blacksquare\)
备注
如前所示，当样本量为
\(n = \frac{(2z_{\alpha/2})^2}{b^2} \cdot p(1-p)\)
时，\(p\) 的 \(100(1-\alpha)\%\) 置信区间的长度将近似为 \(b\)。
现在很容易证明，对于函数 \(g(p) = p(1-p)\)（定义域为：\(0 \leq p \leq 1\)）而言，当 \(p = \frac{1}{2}\) 时，\(g(p)\) 取得最大值 \(\frac{1}{4}\)。因此，\(n\) 的上界为
\(n \leq \frac{(z_{\alpha/2})^2}{b^2}\)
因此，样本量至少为 \(\frac{(z_{\alpha/2})^2}{b^2}\) 时，可以确保在不需要任何额外的抽样的情况下，置信区间的长度不超过 \(b\)。
表 7.3 对本节的内容进行了总结。
| 置信区间类型 | 置信区间 |
|---|---|
| 双边置信区间 | \(\hat{p} \pm z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\) |
| 单边下置信区间 | \(\left(-\infty, \, \hat{p} + z_{\alpha} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right)\) |
| 单边上置信区间 | \(\left(\hat{p} - z_{\alpha} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \, \infty\right)\) |