随机变量
当执行随机实验时,我们并不总是对实验结果的全部细节都感兴趣,我们仅对由结果确定的某些 数值量 (numerical quantity )的值感兴趣。例如,在抛骰子时,对于每个骰子的点数而言,我们并不感兴趣;我们通常对两个骰子的点数之和感兴趣。也就是说,我们可能想知道点数总和是 7 的情况,而并不关心实际结果是否是:(1, 6)、(2, 5)、(3, 4)、(4, 3)、(5, 2)、(6, 1)。此外,对于土木工程师而言,他们可能不关心水库水位的日常涨落(我们可以将水库水位的日常涨落数据视为实验结果),他们只关心雨季结束时的水位。由实验结果确定的我们感兴趣的这些 量化指标 (quantities ),我们称为 随机变量 (random variables )。
因为 随机变量 的值是由实验结果确定的,因此,对于 随机变量 的可能的值,我们可以对其给与概率赋值。
例 4.1 \(X\) 表示随机变量:抛 2 个骰子的点数之和,则:
\[
\begin{align}
P\{X=2\} &= P(\{(1,1)\}) = \frac{1}{36} \\
P\{X=3\} &= P(\{(1,2), (2,1)\}) = \frac{2}{36} \\
P\{X=4\} &= P(\{(1,3), (2,2), (3,1)\}) = \frac{3}{36} \\
P\{X=5\} &= P(\{(1,4), (2,3), (3,2), (4,1)\}) = \frac{4}{36} \\
P\{X=6\} &= P(\{(1,5), (2,4), (3,3), (4,2), (5,1)\}) = \frac{5}{36} \\
P\{X=7\} &= P(\{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}) = \frac{6}{36} \\
P\{X=8\} &= P(\{(2,6), (3,5), (4,4), (5,3), (6,2)\}) = \frac{5}{36} \\
P\{X=9\} &= P(\{(3,6), (4,5), (5,4), (6,3)\}) = \frac{4}{36} \\
P\{X=10\} &= P(\{(4,6), (5,5), (6,4)\}) = \frac{3}{36} \\
P\{X=11\} &= P(\{(5,6), (6,5)\}) = \frac{2}{36} \\
P\{X=12\} &= P(\{(6,6)\}) = \frac{1}{36}
\end{align}
\tag{4.1}\]
换句话说,随机变量 \(X\) 的取值为 2~12 之间的任何整数值,其每个取值的概率由 式 4.1 给出。由于 \(X\) 必须为某个取值,因此我们必有:
\[
1 = P(S) = P\Bigg( \bigcup_{i=2}^{12}{\{X=i\}} \Bigg) = \sum_{i=2}^{12}{P\{X=i\}}
\tag{4.2}\]
利用 式 4.1 可以非常简单的验证 式 4.2 。
在这个实验中,我们感兴趣的另一个 随机变量 是第一个骰子的点数。令 \(Y\) 表示 随机变量 :抛两个骰子时第一个骰子的点数。则 \(Y\) 的取值为 1~6 之间的任何值。也就是说:
\[
P\{Y=i\} = \frac{1}{6}, i=1,2,3,4,5,6 \quad \blacksquare
\tag{4.3}\]
例 4.2 d 表示)或者没有缺陷(用 a 表示)。则这两个电子元器件有四种可能的结果:(d, d)、(d, a)、(a, d)、(a, a),假设 这四种结果的概率分别为:0.09、0.21、0.21、0.49(其中 (d, d) 表示两个元器件都有缺陷,(d, a) 表示第一个元器件有缺陷、第二个元件没有缺陷,依此类推)。
我们令 \(X\) 表示购买的两个电子元器件中没有缺陷的元器件数量,那么 \(X\) 是一个 随机变量 ,且其取值为 0、1、2 中的一个:
\[
\begin{align}
P\{X=0\} &= 0.09 \\
P\{X=1\} &= 0.42 \\
P\{X=2\} &= 0.49
\end{align}
\tag{4.4}\]
如果我们主要关注这两个电子元器件是否至少有一个没有缺陷,则我们可以对 随机变量 \(I\) 作如下定义:
\[
I = \begin{cases}
1, \quad & if \ X=1, 2 \\
0, \quad & if \ X=0
\end{cases}
\tag{4.5}\]
如果 \(A\) 表示事件:至少一个元器件没有缺陷,则根据 \(A\) 是否发生,\(I\) 将等于 1 或 0。因此,我们称 随机变量 \(I\) 为 事件 \(A\) 的 指示随机变量 (indicator random variable )。\(I\) 的可能取值的概率为:
\[
\begin{align}
&P\{I=1\}=0.91 \\
&P\{I=0\}=0.09 \qquad \blacksquare
\end{align}
\tag{4.6}\]
在 例 4.1 和 例 4.2 这两个例子中,我们感兴趣的 随机变量 的可能取值的数量是有限的。对于那些取值可以写成有限序列 \(x_1,..., x_n\) 或者无限序列 \(x_1,...\) 的 随机变量 称为 离散随机变量 (discrete random variables )。例如,一个取值集合为非负整数的 随机变量 就是 离散随机变量 。然而,也存在取值为连续数值的 随机变量 ,我们称这种 随机变量 为 连续随机变量 (continous random variables )。例如,假定汽车的寿命位于某个区间 \((a,b)\) 时,表示汽车寿命的 随机变量 就是 连续随机变量 。
随机变量 \(X\) 的累积分布函数(cumulative distribution function )\(F\) 的定义如下:
\[
F(x) = P\{X \le x\}
\tag{4.7}\]
也就是说,\(F(x)\) 是 随机变量 \(X\) 取值小于或等于 \(x\) 的概率。
随机变量 的累积分布函数也可简称为 分布函数 (distribution function )。
我们将使用 \(X \thicksim F\) 来表示 \(F\) 是 随机变量 \(X\) 的分布函数。
我们可以用 随机变量 \(X\) 的分布函数 \(F\) 来回答所有关于 \(X\) 的概率问题。例如,假如我们想计算 \(P\{a \lt X \le b\}\) 。要计算该概率,我们首先注意到 事件 \({X \le b}\) 可以表示为两个 互斥事件 \({X \le a}\) 和 \({a \lt X \le b}\) 的并集。因此,根据 公理3 (小节 3.4
\[
\begin{align}
P\{X \le b\}&=P\{X \le a\} + P\{a \lt X \le b\} \\
\therefore P\{a \lt X \le b\} &= F(b) - F(a)
\end{align}
\tag{4.8}\]
习题 4.1 随机变量 \(X\) 的分布函数为:
\[
F(x) = \begin{cases}
0, \quad & x \le 0 \\
1-e^{-x^2}, \quad & x \gt 0
\end{cases}
\]
计算 \(P\{X \gt 1\}\) ?
解 4.1 . \[
\begin{align}
P\{X \gt 1\} &= 1 - P\{X \le 1\} \\
&= 1 - F(1) \\
&= e^{-1} \\
&= 0.368 \qquad \blacksquare
\end{align}
\]
随机变量的类型
如前所述,取值为一个序列集的 随机变量 称为 离散随机变量 。对于 离散随机变量 \(X\) ,我们定义其 概率质量函数 \(p(a)\) (probability mass function )为:
\[
p(a) = P\{X=a\}
\tag{4.9}\]
对于 \(a\) 的可数个取值,其 概率质量函数 \(p(a)\) 为正数。也就是说,如果 \(X\) 的取值必须为 \(x_1,x_2,...,x_n\) ,则 \(p(x_i) \gt 0\) ,\(i=1,2,...\) ;对于其他的取值,\(p(x)=0\) 。
因为 \(X\) 必须为 \(x_i\) 中的某个值,所以 \(\sum_{i=1}^{\infty}{p(x_i)}=1\) 。
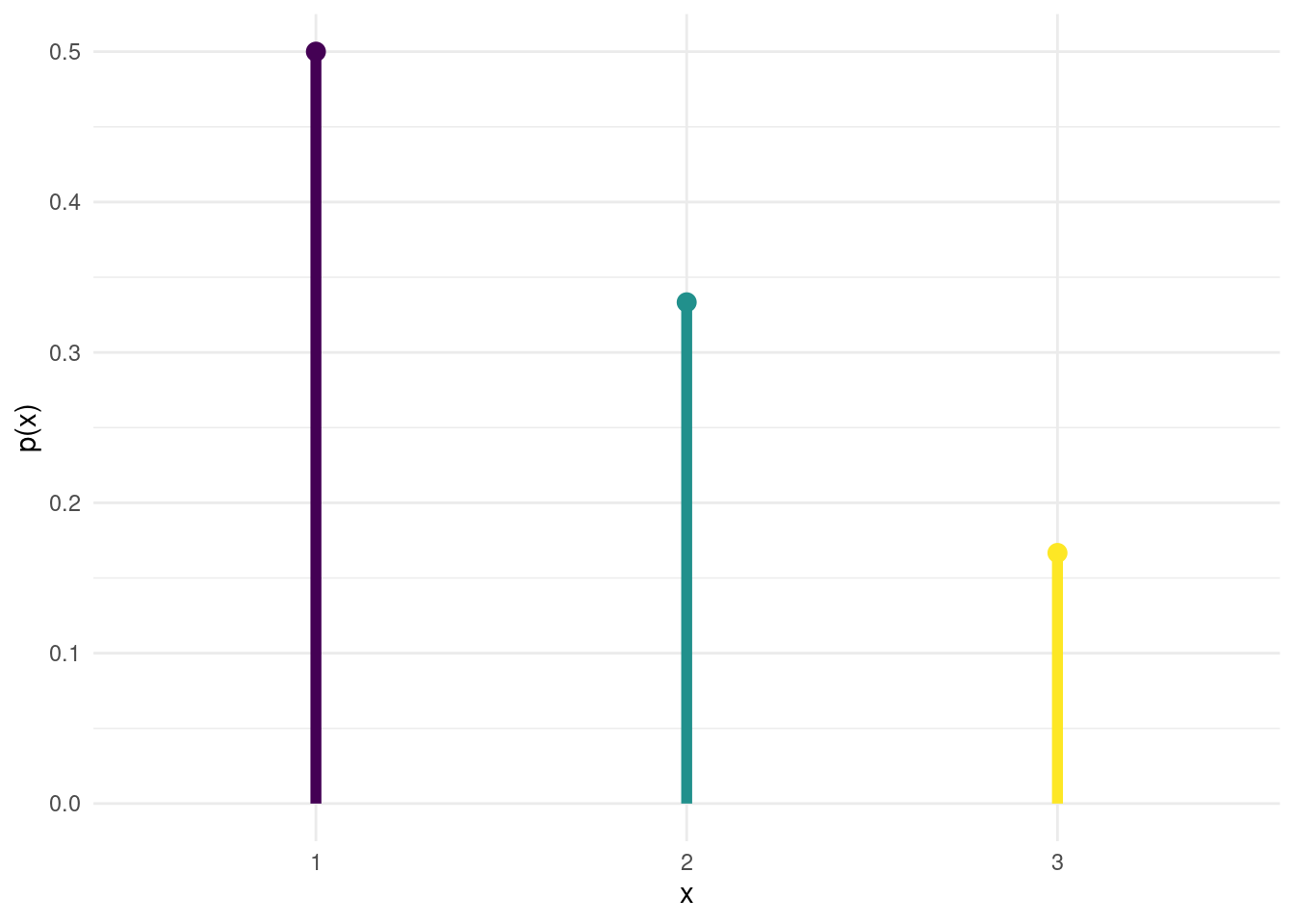
例 4.3 随机变量 \(X\) = 1,2,3,如果已知:\(p(1)=\frac{1}{2}\) ,\(p(2)=\frac{1}{3}\) ,则 \(p(3)=\frac{1}{6}\) 。\(p(x)\) 的线图如 图 4.1 。 \(\blacksquare\)
代码
library (ggplot2)<- data.frame (value = c (1 , 2 , 3 ),p = c (1 / 2 , 1 / 3 , 1 / 6 ),start = rep (0 , 3 )$ value <- factor (df$ value, levels = df$ value, ordered = TRUE )ggplot (df, aes (x = value, y = start, yend = p, color = value)) + geom_segment (size = 2 ) + # 绘制水平线表示每个“条形” geom_point (aes (y = p), size = 3 ) + # 在每个“条形”的末端添加点 theme_minimal () + labs (x = "x" , y = "p(x)" ) + scale_y_continuous (breaks = seq (0 , 1 , by = 0.1 )) + theme (legend.position = "none" ) # 调整图例位置
可以使用 \(p(x)\) 来表示 随机变量 \(X\) 的累积分布函数 \(F\) :
\[
F(a) = \sum_{all \ x \le a}{p(x)}
\tag{4.10}\]
如果 \(X\) 是一个离散随机变量,其可能的取值是 \(x_1,x_2,x_3,...\) ,其中 \(x_1<x_2<x_3<...\) ,那么 \(X\) 的分布函数 \(F\) 是一个阶跃函数(step function )。也就是说,\(F\) 的值在区间 \([x_{i−1},x_i)\) 是恒定的,然后在 \(x_i\) 处有大小为 \(p(x_i)\) 的跃变。
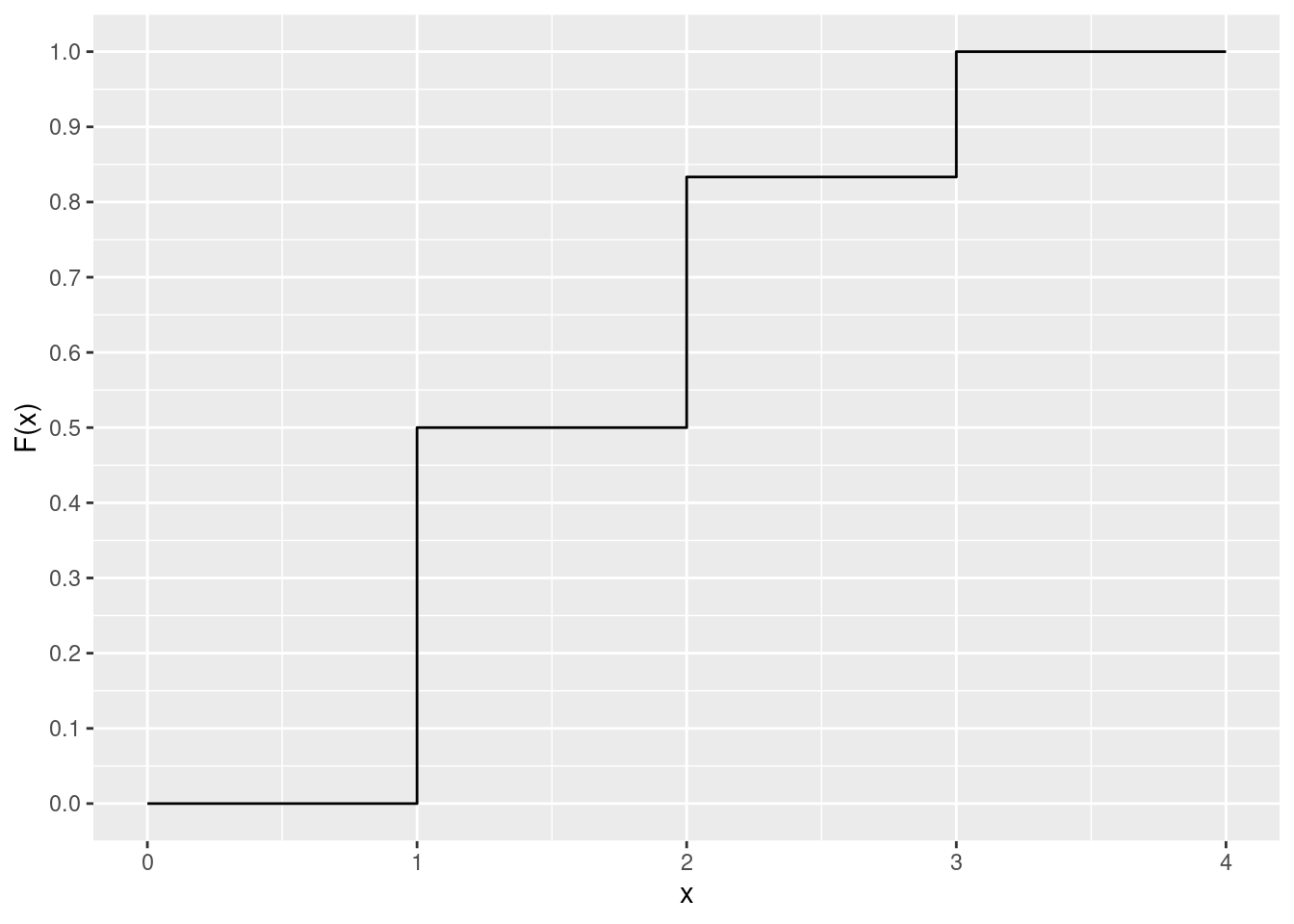
例如,假设 \(X\) 的概率质量函数(如 例 4.3 )为:\(p(1)=\frac{1}{2}\) ,\(p(2)=\frac{1}{3}\) ,\(p(3)=\frac{1}{6}\) 。则 \(X\) 的累积分布函数 \(F\) 为:
\[
F(a) = \begin{cases}
0, \quad & a \lt 1 \\
\frac{1}{2}, \quad & 1 \le a \lt 2 \\
\frac{5}{6}, \quad & 2 \le a \lt 3 \\
1, \quad & 3 \le a
\end{cases}
\tag{4.11}\]
式 4.11 如 图 4.2 所示。
代码
library (ggplot2)<- data.frame (value = c (1 , 2 , 3 ),p = c (1 / 2 , 1 / 3 , 1 / 6 )$ cpf <- cumsum (df$ p)<- data.frame (value = c (0 , 1 , 1 , 2 , 2 , 3 , 3 , 4 ),cpf = c (0 , 0 , df$ cpf[1 ], df$ cpf[1 ], df$ cpf[2 ], df$ cpf[2 ], df$ cpf[3 ], df$ cpf[3 ])#df1$value <- factor(df$value, levels = df$value, ordered = TRUE) ggplot (df1, aes (x = value, y = cpf)) + geom_line () + labs (x = "x" , y = "F(x)" ) + scale_y_continuous (breaks = seq (0 , 1 , by = 0.1 )) + theme (legend.position = "none" ) # 调整图例位置
离散随机变量 的可能取值是一个序列集合,但是我们通常必须考虑那些取值是一个区间的 随机变量 。假设 \(X\) 为一个取值是一个区间的 随机变量 。如果存在一个定义域为所有实数 \(x \in (−\infty, \infty)\) 的非负函数 \(f(x)\) ,且对于任意实数集 \(B\) ,\(f(x)\) 都满足:
\[
P\{X \in B\} = \int_{B}{f(x)\mathrm{d} x}
\tag{4.12}\]
则我们称 \(X\) 是一个 连续随机变量 (continous random variable ),而函数 \(f(x)\) 为 随机变量 \(X\) 的 概率密度函数 (probability density function )。
换句话说,式 4.12 指出,对集合 \(B\) 上的概率密度函数进行积分运算可以得到 \(X\) 在 \(B\) 中的概率。由于 \(X\) 必须为某个值,所以 \(f(x)\) 必须满足:
\[
1 = P\{X \in (-\infty, \infty)\} = \int_{-\infty}^{\infty}{f(x)\mathrm{d} x}
\tag{4.13}\]
概率密度函数 \(f(x)\) 可以用于回答所有关于 随机变量 \(X\) 的概率问题,例如,令 \(B=[a,b]\) ,根据 式 4.12 ,我们有:
\[
P\{a \le X \le b\}=\int_{a}^{b}{f(x)\mathrm{d} x}
\tag{4.14}\]
在 式 4.14 中,如果令 \(a=b\) ,则:
\[
P\{X=a\}=\int_{a}^{a}{f(x)\mathrm{d} x} = 0
\tag{4.15}\]
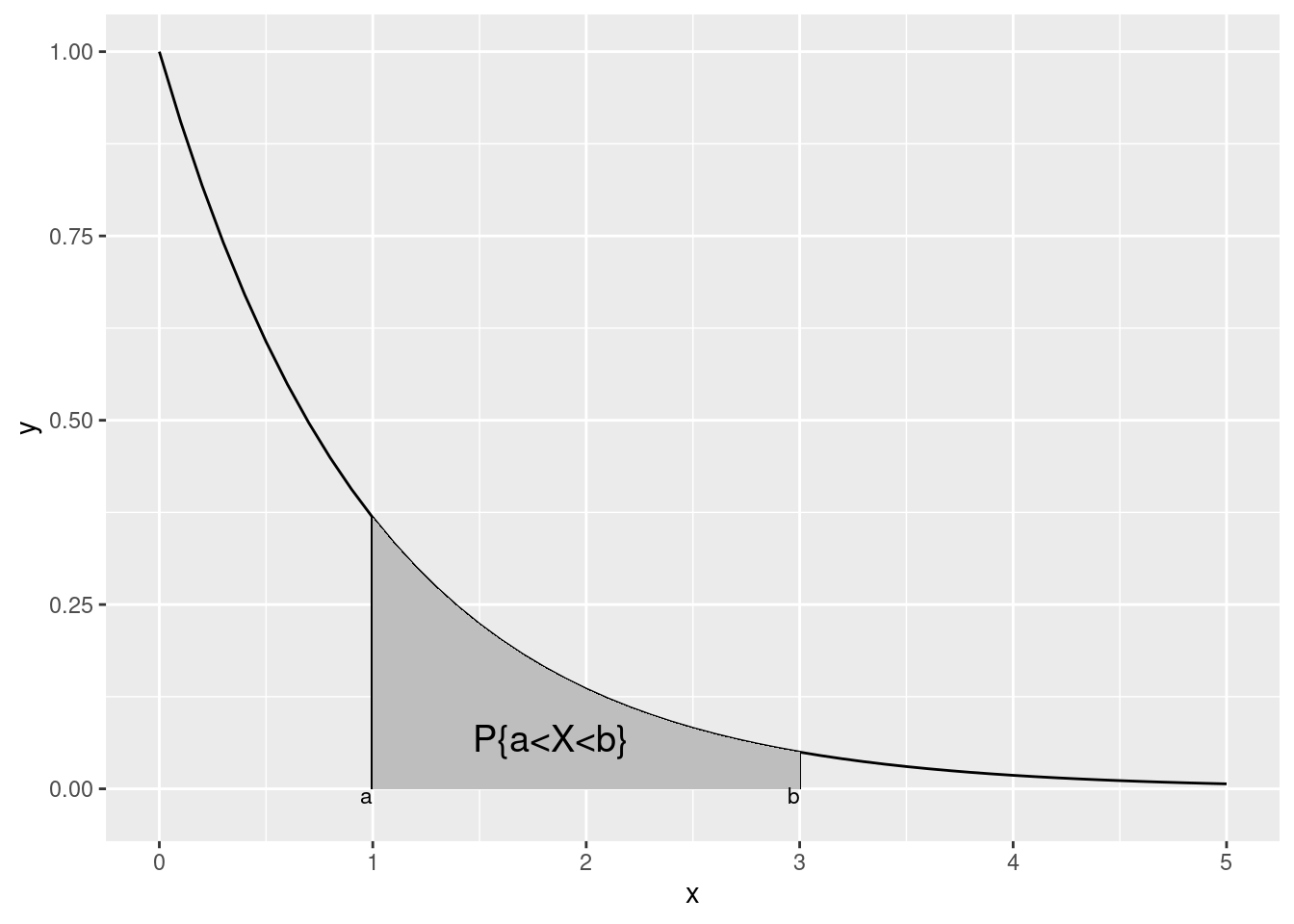
换句话说,对于 连续随机变量 而言,其取值为某个特殊值的概率为 0,如 图 4.3 所示。
代码
library (ggplot2)<- seq (0 , 5 , 0.1 )<- exp (- x)<- data.frame (x= x, y= y)ggplot (df, aes (x= x, y= y)) + geom_line () + geom_segment (x= 1 , y= exp (- 1 ), xend= 1 , yend= 0 ) + geom_segment (x= 3 , y= exp (- 3 ), xend= 3 , yend= 0 ) + geom_ribbon (data = subset (df, x >= 1 & x <= 3 ), aes (ymin = 0 , ymax = y), fill = "gray" ) + annotate ("text" , x = 1 , y = - 0.02 , label = "a" , hjust = 1 , vjust = 0 , size = 3 ) + annotate ("text" , x = 3 , y = - 0.02 , label = "b" , hjust = 1 , vjust = 0 , size = 3 ) + annotate ("text" , x = 2.2 , y = 0.05 , label = "P{a<X<b}" , hjust = 1 , vjust = 0 , size = 5 )
连续随机变量的概率是其密度函数 \(f(x)\) 在某个区间上积分的结果,因此对于某个特殊的取值,其结果必然为 0。
累积分布函数 \(F(\cdot)\) 和概率密度函数 \(f(\cdot)\) 之间的关系如下所示:
\[
\begin{align}
F(a)&=P\{X \in (-\infty,a]\} = \int_{-\infty}^{a}{f(x)\mathrm{d} x} \\
两边&求微分得:\\
\frac{dF(a)}{da}&=f(a)
\end{align}
\tag{4.16}\]
也就是说,概率密度函数是累积分布函数的导数。根据 式 4.14 ,概率密度函数的更直观的解释如下:
\[
P\{a - \frac{\varepsilon}{2} \le X \le a + \frac{\varepsilon}{2}\} = \int_{a-\frac{\varepsilon}{2}}^{a+\frac{\varepsilon}{2}}{f(x)\mathrm{d} x} \approx \varepsilon f(a)
\tag{4.17}\]
其中,\(\varepsilon\) 是一个非常小的数。也就是说,\(X\) 的取值位于区间 \([a - \frac{\varepsilon}{2},a + \frac{\varepsilon}{2}]\) 内时的概率大约为 \(\varepsilon f(a)\) 。由此,我们可以看出,\(f(a)\) 是对随机变量 \(X\) 的取值接近 \(a\) 的可能性大小的一种度量。
习题 4.2 \(X\) 是一个连续随机变量,其概率密度函数为:
\[
f(x)=\begin{cases}
C(4x - 2x^2), \quad &0 \lt x \lt 2 \\
0, \quad &其它
\end{cases}
\]
则:
计算 \(C\) 的值?
计算 \(P\{X \gt 1\}\) ?
解 4.2 . \(f(x)\) 是一个概率密度函数,因此必有:\(\int_{-\infty}^{\infty}{f(x)\mathrm{d} x}=1\) 。因此,有:
\[
\begin{align}
C\int_0^2{(4x-2x^2)\mathrm{d} x} &=1 \\
C\bigg(2x^2-\frac{2}{3}x^3\bigg)\Bigg|_{x=0}^{x=2} &= 1
\end{align}
\]
所以,\(C = \frac{3}{8}\) 。所以,\(P\{X \gt 1\}=\int_{1}^{\infty}{f(x)\mathrm{d} x}=\frac{3}{8}\int_1^2{(4x-2x^2)\mathrm{d} x}=\frac{1}{2}\) 。 \(\blacksquare\)
联合分布
对于一个给定的实验,我们不仅对单个 随机变量 的概率分布函数感兴趣;对两个或多个 随机变量 之间的关系,我们同样感兴趣。例如,在一项关于癌症可能原因的实验中,我们可能对每天平均吸烟数量与个体患癌症年龄之间的关系感兴趣。同样,工程师可能对钢板样品的抗剪强度和点焊直径之间的关系感兴趣。
为了描述两个 随机变量 之间的关系,我们定义 \(X\) 和 \(Y\) 的联合累积概率分布函数(joint cumulative probability distribution function ):
\[
F(x,y) = P\{X \le x,Y \le y\}
\tag{4.18}\]
至少在理论上,可以根据联合概率分布函数来计算任何关于 \(X\) 和 \(Y\) 的概率。例如,可以从 \(X\) 和 \(Y\) 的联合分布函数 \(F\) 中得到 \(X\) 的分布函数 \(F_X\) :
\[
\begin{align}
F_X(x) &= P\{X \le x\} \\
&= P\{X \le x, Y \le \infty \} \\
&= F(x, \infty)
\end{align}
\tag{4.19}\]
同理,\(Y\) 的累积分布函数为 \(F_Y(y) = F(\infty, y)\) 。
如果 \(X\) 和 \(Y\) 都是 离散随机变量 ,且其可能的取值分别为:\(x_1, x_2, ...\) 和 \(y_1, y_2, ...\) ,定义 \(X\) 和 \(Y\) 的联合概率质量函数(joint probability mass function )\(p(x_i, y_j)\) 为:
\[
p(x_i, y_j) = P\{X = x_i, Y = y_j\}
\tag{4.20}\]
由于 \(Y\) 必须取某个值 \(y_j\) ,并且所有的 \(y_j\) 之间都是 互斥事件 ,因此 事件 \(\{X = x_i\}\) 可以写作 \(\{X = x_i, Y = Y_j\}\) 在所有 \(j\) 上的并集。即:
\[
\{X = x_i\} = \bigcup_{all\ j}{\{X = x_i, Y = y_j\}}
\tag{4.21}\]
根据 公理3 (小节 3.4
\[
\begin{align}
P\{X = x_i\} &= P\bigg(\bigcup_{all\ j}{\{X = x_i, Y = y_j\}}\bigg) \\
&= \sum_{all \ j}{P\{X = x_i, Y = y_j\}} \\
&= \sum_{all \ j}{p(x_i, y_j)}
\end{align}
\tag{4.22}\]
同理,我们可以得到 \(P\{Y = y_j\}\) :
\[
\begin{align}
P\{Y = y_i\} &= \sum_{all \ i}{P\{X = x_i, Y = y_j\}} \\
&= \sum_{all \ i}{p(x_i, y_j)}
\end{align}
\tag{4.23}\]
因此,随机变量 的联合概率质量函数总是可以决定单个 随机变量 的概率质量函数。然而,需要注意的是:反之,并不成立。即,即便知道 \(P\{X = x_i\}\) 和 \(P\{Y = y_j\}\) 的值也不能决定 \(P\{X = x_i, Y = y_j\}\) 的值。
例 4.4 \(X\) 为抽取的电池中的新电池的数量,令 \(Y\) 为抽取的电池中用过但还有电量的电池的数量。则 \(X\) 和 \(Y\) 的联合概率质量函数 \(p(i, j) = P\{X = i, Y = j\}\) 为:
\[
p(i, j) = \frac{\left(\begin{array}{cc} 3 \\ i \end{array}\right) \left(\begin{array}{cc} 4 \\ j \end{array}\right) \left(\begin{array}{cc} 5 \\ 3 - i -j \end{array}\right) }{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)}
\]
从 12 块电池里随机抽取 3 块电池的抽取方式为 \(\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)\) 。根据 小节 3.5.1 计数基本原理 ,抽取的 3 块电池中恰好有 \(i\) 块新电池、\(j\) 块用过但还有电量的电池、\(3 - i - j\) 块没有电量的电池的抽取方式为 \(\left(\begin{array}{cc} 3 \\ i \end{array}\right) \left(\begin{array}{cc} 4 \\ j \end{array}\right) \left(\begin{array}{cc} 5 \\ 3 - i -j \end{array}\right)\) 。因此:
\[
\begin{align}
p(0, 0) &= \frac{\left(\begin{array}{cc} 5 \\ 3 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{10}{220} \\
p(0, 1) &= \frac{\left(\begin{array}{cc} 4 \\ 1 \end{array}\right) \left(\begin{array}{cc} 5 \\ 2 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{40}{220} \\
p(0, 2) &= \frac{\left(\begin{array}{cc} 4 \\ 2 \end{array}\right) \left(\begin{array}{cc} 5 \\ 1 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{30}{220} \\
p(0, 3) &= \frac{\left(\begin{array}{cc} 4 \\ 3 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{4}{220} \\
p(1, 0) &= \frac{\left(\begin{array}{cc} 3 \\ 1 \end{array}\right) \left(\begin{array}{cc} 5 \\ 2 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{30}{220} \\
p(1, 1) &= \frac{\left(\begin{array}{cc} 3 \\ 1 \end{array}\right) \left(\begin{array}{cc} 4 \\ 1 \end{array}\right) \left(\begin{array}{cc} 5 \\ 1 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{60}{220} \\
p(1, 2) &= \frac{\left(\begin{array}{cc} 3 \\ 1 \end{array}\right) \left(\begin{array}{cc} 4 \\ 2 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{18}{220} \\
p(2, 0) &= \frac{\left(\begin{array}{cc} 3 \\ 2 \end{array}\right) \left(\begin{array}{cc} 5 \\ 1 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{15}{220} \\
p(2, 1) &= \frac{\left(\begin{array}{cc} 3 \\ 2 \end{array}\right) \left(\begin{array}{cc} 4 \\ 1 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{12}{220} \\
p(3, 0) &= \frac{\left(\begin{array}{cc} 3 \\ 3 \end{array}\right)}{\left(\begin{array}{cc} 12 \\ 3 \end{array}\right)} = \frac{1}{220}
\end{align}
\]
可以通过 表 4.1 的表格格式来更简单的表示如上的概率。
读者应该注意,通过计算行的和所得到的 \(X\) 的概率质量函数和 式 4.22 的结果是一致的;同时,通过计算列的和所得到的 \(Y\) 的概率质量函数和 式 4.23 的结果也是一致的。因为 \(X\) 和 \(Y\) 的各自的概率质量函数出现在 表 4.1 所示的联合概率分布表的边缘(margin ),因此,我们又常常称 \(X\) 和 \(Y\) 的各自的概率质量函数为 边缘概率质量函数 (marginal probability mass function )。应该注意的是,为了检查类似 表 4.1 这样的表的正确性,我们可以对表中的最后一行(或最右一列)求和,并验证其结果是否为 1。(为什么最后一行或最右一列的和必须等于 1?) \(\blacksquare\)
例 4.5
如果从这个社区中随机选择一个家庭,那么这个家庭中男孩的数量 \(B\) 和女孩的数量 \(G\) 具有 表 4.2 所示的联合概率质量函数。
于是,我们可以得到如下的概率:
\[
\begin{align}
P\{B=0, G=0\} &= P\{没有孩子\} = 0.20 \cdot \frac{1}{2} = 0.15 \\
P\{B=0, G=1\} &= P\{有 1 个孩子且为女孩\} = 0.35 \cdot (\frac{1}{2})^2 = 0.1 \\
P\{B=0, G=3\} &= P\{有 3 个孩子且都为女孩\} = = 0.30 \cdot (\frac{1}{2})^3 = 0.0375 \\
\end{align}
\]
您可以验证 表 4.2 的其余部分,通过 表 4.2 我们可以知道,所选择的家庭至少有一个女孩的概率为 0.625(\(1-P\{B=i, G=0\}\) )。\(\blacksquare\)
\(X\) 和 \(Y\) 是两个连续 随机变量 ,对于 \(x \in (-\infty, \infty)\) 和 \(y \in (-\infty, \infty)\) ,对于任何一个 \(x\) 和 \(y\) 构成的 数据对 集合 \(C\) (\(C\) 是一个二维平面中的集合),如果存在函数 \(f(x,y)\) ,使得:
\[
P\{(X,Y) \in C\} = \iint_{(x,y) \in C}{f(x,y)\mathrm{d} x \mathrm{d} y}
\tag{4.24}\]
我们称 \(X\) 和 \(Y\) 是联合连续随机变量,称函数 \(f(x,y)\) 为 \(X\) 和 \(Y\) 的 联合概率密度函数 (joint probability density function )。如果令 \(A\) 和 \(B\) 为两个实数集,并令 \(C = \{(x,y): x \in A, y \in B\}\) ,则 式 4.24 可以写作:
\[
P\{X \in A, Y \in B\} = \int_{B} \int_{A} {f(x,y)\mathrm{d} x \mathrm{d} y}
\tag{4.25}\]
因为:
\[
\begin{align}
F(a,b) &= P\{X \in (-\infty, a], Y \in (-\infty, b]\} \\
&= \int_{-\infty}^{b} \int_{-\infty}^{a} {f(x,y)\mathrm{d} x \mathrm{d} y}
\end{align}
\tag{4.26}\]
所以,对 式 4.26 两边微分得到:
\[
\frac{\partial^{2}{F(a,b)}}{\partial a \ \partial b} = f(a,b)
\tag{4.27}\]
也就是说,联合概率密度函数 \(f(\cdot)\) 是联合概率分布函数 \(F(\cdot)\) 的偏微分。根据 式 4.25 ,我们有:
\[
\begin{align}
P\{a \lt X \lt a + \Delta a, b \lt Y \lt b + \Delta b\} &= \int_{b}^{b + \Delta b} \int_{a}^{a + \Delta a} {f(x,y)\mathrm{d} x \mathrm{d} y} \\
&\approx f(a,b) \Delta a \Delta b
\end{align}
\tag{4.28}\]
因为 \(\Delta a\) 和 \(\Delta b\) 都是非常小的数,并且 \(f(x,y)\) 在 \((a,b)\) 处是连续的。因此 \(f(a,b)\) 是对 \((X,Y)\) 靠近 \((a,b)\) 的可能性大小的一种度量。
如果 \(X\) 和 \(Y\) 是联合连续随机变量,则 \(X\) 和 \(Y\) 各自都是连续随机变量,则 \(X\) 的概率密度函数为:
\[
\begin{align}
P\{X \in A\} &= P\{X \in A, Y \in (-\infty, \infty)\} \\
&= \int_{A} \int_{-\infty}^{\infty} {f(x,y) \mathrm{d} y\mathrm{d} x} \\
&= \int_{A}{f_X{(x)\mathrm{d} x}} \\
其中\ f_X{(x)} &= \int_{-\infty}^{\infty}{f(x,y) \mathrm{d} y}
\end{align}
\tag{4.29}\]
同理,\(Y\) 的概率密度函数为:
\[
\begin{align}
P\{Y \in B\} &= P\{X \in (-\infty, \infty), Y \in B\} \\
&= \int_{B} \int_{-\infty}^{\infty} {f(x,y)\mathrm{d} x \mathrm{d} y} \\
&= \int_{B}{f_Y{(y) \mathrm{d} y}} \\
其中\ f_Y{(y)} &= \int_{-\infty}^{\infty}{f(x,y)\mathrm{d} x}
\end{align}
\tag{4.30}\]
习题 4.3 \(X\) 和 \(Y\) 的联合概率密度函数如下:
\[
f(x,y) = \begin{cases}
2e^{-x}e^{-2y}, \quad & 0 \lt x \lt \infty, 0 \lt y \lt \infty \\
0, \quad & otherwise
\end{cases}
\]
计算:
\(P\{X \gt 1, Y \lt 1\}\) \(P\{X \lt Y\}\) \(P\{X \lt a\}\)
解 4.3 .
\[
\begin{align}
P\{X \gt 1, Y \lt 1\} &= \int_{0}^{1} \int_{1}^{\infty} {2e^{-x}e^{-2y}\mathrm{d} x \mathrm{d} y} \\
&= \int_{0}^{1}{2e^{-2y}(-e^{-x} \big |_{1}^{\infty})} \mathrm{d} y \\
&= e^{-1}\int_{0}^{1}2e^{-2y} \mathrm{d} y \\
&= e^{-1}(1-e^{-2})
\end{align}
\]
\[
\begin{align}
P\{X \lt Y\} &= \iint_{(x,y):x \lt y}{2e^{-x}e^{-2y}\mathrm{d} x \mathrm{d} y} \\
&= \int_{0}^{\infty} \int_{0}^{y} {2e^{-x}e^{-2y}\mathrm{d} x \mathrm{d} y} \\
&= \int_{0}^{\infty}{2e^{-2y}(1-e^{-y}) \mathrm{d} y} \\
&= \int_{0}^{\infty}{2e^{-2y} \mathrm{d} y} - \int_{0}^{\infty}{2e^{-3y} \mathrm{d} y} \\
&= 1-\frac{2}{3} \\
&= \frac{1}{3}
\end{align}
\]
\[
\begin{align}
P\{X \lt a\} &= \int_{0}^{a} \int_{0}^{\infty}{2e^{-2y}e^{-x} \mathrm{d} y\mathrm{d} x} \\
&= \int_{0}^{a}{e^{-x}\mathrm{d} x} \\
&= 1-e^{-a}
\end{align}
\]
\(\blacksquare\)
独立随机变量
对于任意的两个实数集 \(A\) 和 \(B\) ,如果随机变量 \(X\) 和 \(Y\) 满足 式 4.31 ,我们称 \(X\) 和 \(Y\) 是相互独立的。
\[
P\{X \in A, Y \in B\} = P\{X \in A\}P\{Y \in B\}
\tag{4.31}\]
换句话说,对于所有的 \(A\) 、\(B\) ,如果事件 \(E_A={X \in A}\) 和 \(E_B={Y \in B}\) 是相互独立的,那么 随机变量 \(X\) 和 \(Y\) 也是相互独立的。
根据 小节 3.4 三大公理 ,对于所有的 \(a\) 、\(b\) ,式 4.31 满足:
\[
P\{X \le a, Y \le b\} = P\{X \le a\}P\{Y \le b\}
\tag{4.32}\]
因此,就 \(X\) 和 \(Y\) 的联合分布函数 \(F\) 而言,如果 \(F(a,b) = F_X(a)F_Y(b)\) ,则 \(X\) 和 \(Y\) 是独立的。
当 \(X\) 和 \(Y\) 是离散随机变量时,式 4.31 等价于:
\[
p(x,y)=p_X{(x)}p_Y{(y)} \quad for \ all \ x,y
\tag{4.33}\]
其中,\(p_X\) 和 \(p_Y\) 分别为 \(X\) 和 \(Y\) 的概率质量函数。
如果 式 4.31 成立,那么我们令 \(A={x}\) ,\(B={y}\) ,于是我们能够得到 式 4.33 。此外,如果 式 4.33 成立,那么对于任何集合 \(X \in A\) 、\(Y \in B\) ,都有:
\[
\begin{align}
P\{X \in A, Y \in B\} &= \sum_{y \in B}\sum_{x \in A}{p(x,y)} \\
&= \sum_{y \in B}\sum_{x \in A}{p_X{(x)}p_Y{(y)}} \\
&= \sum_{y \in B}{p_Y{(y)}} \sum_{x \in A}{p_X{(x)}} \\
&= P\{Y \in B\}P\{X \in A\} \\
&= P\{X \in A\}P\{Y \in B\}
\end{align}
\]
即,式 4.33 成立也意味着 式 4.31 成立。因此,式 4.31 和 式 4.33 是等价的。
同理,当 \(X\) 和 \(Y\) 是连续随机变量时,式 4.31 等价于:对于所有的 \(x\) 、\(y\) ,都有 \(f(x,y) = f_X(x)f_Y(y)\) 。如果一个随机变量 \(X\) 的取值不会改变另一个随机变量 \(Y\) 的分布,那么我们可以大致认为 \(X\) 和 \(Y\) 是独立的。不独立的随机变量称为 依赖随机变量 。
习题 4.4 \(X\) 和 \(Y\) 是两个独立随机变量,其概率密度函数均为:
\[
f(x)=\begin{cases}
e^{-x}, \quad & x \gt 0 \\
0, \quad & otherwise
\end{cases}
\]
求 随机变量 \(\frac{X}{Y}\) 的概率密度函数?
解 4.4 . \(\frac{X}{Y}\) 的概率分布函数 \(F\) :
\[
\begin{align}
\forall a & \gt 0, \\
F_{\frac{X}{Y}}{(a)} &= P\{\frac{X}{Y} \le a\} \\
&= \iint_{\frac{x}{y} \le a}{f(x,y)\mathrm{d} x \mathrm{d} y} \\
&= \iint_{\frac{x}{y} \le a}{e^{-x}e^{-y}\mathrm{d} x \mathrm{d} y} \\
&= \int_{0}^{\infty} \int_{0}^{ay} {e^{-x}e^{-y}\mathrm{d} x \mathrm{d} y} \\
&= \int_{0}^{\infty} {(1-e^{-ay})e^{-y} \mathrm{d} y} \\
&= \bigg(-e^{-y} + \frac{e^{-(a+1)y}}{a+1}\bigg) \bigg | _{0}^{\infty} \\
&= 1 - \frac{1}{a+1}
\end{align}
\]
对 \(F_{\frac{X}{Y}}{(a)}\) 求导得到 \(f_{\frac{X}{Y}(a)} = \frac{1}{(1+a)^2}\) 。 \(\blacksquare\)
我们可以用定义 2 个 随机变量 的联合概率分布函数的方式来定义 \(n\) 个 随机变量 的联合概率分布函数。对于 \(n\) 个 随机变量 \(X_1,X_2,...,X_n\) ,其联合累积概率分布函数 \(F(a_1,a_2,...,a_n)\) 为:
\[
F(a_1,a_2,...,a_n) = P\{X_1 \le a_1, X_2 \le a_2,..., X_n \le a_n\}
\tag{4.34}\]
对于离散随机变量,则其联合概率质量函数 \(p(x_1,x_2,...,x_n)\) 为:
\[
p(x_1,x_2,...,x_n) = P\{X_1=x_1, X_2=x_2,..., X_n=x_n\}
\tag{4.35}\]
此外,对于 \(n\) 维空间中的集合 \(C\) ,如果存在一个函数 \(f(\cdot)\) 使得:
\[
P\{(X_1,X_2,...,X_n) \in C\} = \idotsint_{(x_1,...,x_n) \in C}{f(x_1,...,x_n)\mathrm{d} x_1 \cdots \mathrm{d} x_n}
\tag{4.36}\]
我们称 \(f(x_1,...,x_n)\) 为这 \(n\) 个联合连续随机变量的联合概率密度函数。
特殊的,对于任意的 \(n\) 个实数集 \(A_1,A_2,...,A_n\) :
\[
\begin{align}
P\{X_1 \in A_1, X_2 \in A_2, ..., X_n \in A_n\} &= \\
\int_{A_n} \int_{A_{n-1}} \cdots \int_{A_1}{f(x_1,...,x_n)\mathrm{d} x_1\mathrm{d} x_2 \cdots \mathrm{d} x_n} &
\end{align}
\tag{4.37}\]
当然,也可以为两个之上的 随机变量 定义独立性。一般来的,对于 \(n\) 个 随机变量 \(X_1,X_2,...,X_n\) ,如果对于所有实数集 \(A_1,A_2,...,A_n\) 都有:
\[
P\{X_1 \in A_1, X_2 \in A_2, ..., X_n \in A_n\} = \Pi_{i=1}^{n}{P\{X_i \in A_i\}}
\tag{4.38}\]
则我们称这 \(n\) 个随机变量时相互独立的。正如 式 4.31 和 式 4.33 所述,式 4.38 等价于 式 4.39 :
\[
P\{X_1 \le a_1, X_2 \le a_2, ..., X_n \le a_n\} = \Pi_{i=1}^{n}{P\{X_i \in a_i\}}
\tag{4.39}\]
对于一个随机变量的无限集合 \(S\) ,如果 \(S\) 的所有的子集中的 随机变量 均是独立的,我们说 \(S\) 中的所有随机变量之间是相互独立的。(定义 3.3 的一般形式)
例 4.6
\[
P\{第 i 日变化\} = \begin{cases}
-3, \quad &概率为 0.05 \\
-2, \quad &概率为 0.10 \\
-1, \quad &概率为 0.20 \\
0, \quad &概率为 0.30 \\
1, \quad &概率为 0.20 \\
2, \quad &概率为 0.10 \\
3, \quad &概率为 0.05
\end{cases}
\]
令 \(X_i\) 表示第 \(i\) 天的股价变化,那么,这只股票在未来的连续 3 天里,股价分别上涨 1%、2%、0% 的概率为:
\[
P\{X_1=1, X_2=2, X_3=0\} = 0.20 \cdot 0.10 \cdot 0.30 = 0.006 \quad \blacksquare
\]
条件分布
对于两个 随机变量 ,通常可以利用其中一个变量在另一个变量的给定值的情况下的条件分布来确定这两个 随机变量 之间的关系。回顾一下,对于任意两个事件 \(E\) 和 \(F\) ,只要 \(P(F)>0\) ,则在给定 \(F\) 条件下 \(E\) 的条件概率为:
\[
P(E|F)=\frac{P(EF)}{P(F)}
\]
因此,如果 \(X\) 和 \(Y\) 是两个离散随机变量,那么在给定 \(Y=y\) 的条件下,\(X\) 的条件概率质量函数为:
\[
\begin{align}
p_{X|Y}(x|y) &= P\{X=x | Y=y\} \\
&= \frac{P\{X=x, Y=y\}}{P\{Y=y\}} \\
&= \frac{p(x,y)}{p_Y(y)}
\end{align}
\]
其中,对于所有的 \(y\) ,\(p_Y(y) \gt 0\) 。
习题 4.5 例 4.5 中,如果我们知道所选择的这个家庭有 1 个女孩,计算该家庭的小孩中男孩数量的条件概率质量函数。
解 4.5 . 表 4.2 ,\(P\{G=1\}=0.3875\) ,因此,
\[
\begin{align}
P\{B=0 | G=1\} &= \frac{P\{B=0, G=1\}}{P\{G=1\}} = \frac{0.10}{0.3875} = \frac{8}{31} \\
P\{B=1 | G=1\} &= \frac{P\{B=1, G=1\}}{P\{G=1\}} = \frac{0.175}{0.3875} = \frac{14}{31} \\
P\{B=2 | G=1\} &= \frac{P\{B=2, G=1\}}{P\{G=1\}} = \frac{0.1125}{0.3875} = \frac{9}{31} \\
P\{B=3 | G=1\} &= \frac{P\{B=3, G=1\}}{P\{G=1\}} = 0 \\
\end{align}
\]
因此,在有 1 个女孩的条件下,该家庭至少有 1 个男孩的概率为 \(\frac{23}{31}\) 。\(\blacksquare\)
习题 4.6 随机变量 \(X\) 、\(Y\) 的联合概率质量函数 \(p(x,y)\) 为:
\[
p(0,0)=0.4, \quad p(0,1)=0.2, \quad p(1,0)=0.1, \quad p(1,1)=0.3
\]
计算 \(P\{X|Y=1\}\) ?
解 4.6 . \[
\begin{align}
\because\ P\{Y = 1\} &= \sum_{x}p(x,1) = p(0,1) + p(1,1) = 0.5 \\
\therefore\ P\{X=0|Y=1\} &= \frac{p(0,1)}{P\{Y=1\}} = \frac{2}{5} \\
P\{X=1|Y=1\} &= \frac{p(1,1)}{P\{Y=1\}} = \frac{3}{5} \qquad \blacksquare
\end{align}
\]
如果 \(X\) 和 \(Y\) 的联合概率密度函数为 \(f(x,y)\) ,则在 \(Y=y\) 的条件下,\(X\) 的条件概率密度函数为:
\[
f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y{(y)}}, \quad \forall y: \ f_Y(y) \gt 0
\tag{4.40}\]
在 式 4.40 的左边乘以 \(\Delta x\) ,右边乘以 \(\frac{\Delta x \Delta y}{\Delta y}\) 得到:
\[
\begin{align}
f_{X|Y}(x|y) \Delta x &= \frac{f(x,y) \Delta x \Delta y}{f_Y{(y)} \Delta y} \\
& \approx \frac{P\{x \le X \le x + \Delta x, y \le Y \le y + \Delta y\}}{P\{y \le Y \le y + \Delta y\}} \\
&= P\{x \le X \le x + \Delta x\ | y \le Y \le y + \Delta y\}
\end{align}
\tag{4.41}\]
也就是说,对于非常小的 \(\Delta x\) 和 \(\Delta y\) ,\(f_{X|Y}(x|y) \Delta x\) 表示在 \(Y \in [y, y + \Delta y]\) 的条件下,\(X \in [x, x + \Delta x]\) 的条件概率。
我们可以使用条件概率密度函数来定义:在给定一个随机变量的值下,另一个随机变量的条件概率。也就是说,如果 \(X\) 和 \(Y\) 都是连续 随机变量 ,那么,对于任何集合 \(A\) ,都有:
\[
P\{X \in A, Y=y\} = \int_{A}f_{X|Y}(x|y)\mathrm{d} x
\]
习题 4.7 \(X\) 和 \(Y\) 的联合概率密度函数为:
\[
f(x,y) = \begin{cases}
\frac{12}{5}x(2-x-y), \quad & 0 \lt x \lt 1, 0 \lt y \lt 1\\
0, \quad & otherwise
\end{cases}
\]
计算 \(Y=y: 0 \lt y \lt 1\) 下,\(X\) 的条件密度函数 \(f_{X|Y}(x|y)\) 。
解 4.7 . \(0 \lt x \lt 1\) ,\(0 \lt y \lt 1\) ,我们有:
\[
\begin{align}
f_{X|Y}(x|y) &= \frac{f(x,y)}{f_Y(y)} \\
&= \frac{f(x,y)}{\int_{-\infty}^{\infty}{f(x,y)\mathrm{d} x}} \\
&= \frac{x(2-x-y)}{\int_0^1{x(2-x-y)\mathrm{d} x}} \\
&= \frac{x(2-x-y)}{\frac{2}{3} - \frac{y}{2}} \\
&= \frac{6x(2-x-y)}{4-3y} \quad \blacksquare
\end{align}
\]
期望
随机变量 的 期望 (expectation )是概率论中最重要的概念之一。如果 \(X\) 是一个离散 随机变量 ,其可能的取值为 \(x_1\) ,\(x_2\) ,……那么 \(X\) 的 期望 或 期望值 \(E[X]\) 为:
\[
E[X] = \sum_{i}{x_iP\{X = x_i\}}
\tag{4.42}\]
换句话说,\(X\) 的 期望 是其可能取值的加权平均数,其中每个可能取值的权重为该值对应的概率。
例如,如果 \(X\) 的概率质量函数为 \(p(0)=p(1)=\frac{1}{2}\) ,则 \(E[X]\) 只是 \(X\) 的两个可能取值(0、1)的平均数:
\[
E[X] = 0 \cdot \frac{1}{2} + 1 \cdot \frac{1}{2} = \frac{1}{2}
\]
如果 \(p(0)=\frac{1}{3}\) ,\(p(1)=\frac{2}{3}\) ,则 \(E[X]\) 是其两个可能取值(0、1)的加权平均值,其中 1 的权重是 0 的 2 倍(因为 \(p(1)=2p(0)\) ):
\[
E[X] = 0 \cdot \frac{1}{3} + 1 \cdot \frac{2}{3} = \frac{2}{3}
\]
我们也可以利用概率的频率解释(小节 3.1 期望 。概率的评率解释认为,如果独立的重复执行一个实验无数次,那么对于任何事件 \(E\) ,\(E\) 发生的概率 \(P(E)\) 就是其发生的次数的占比。现在,考虑一个随机变量 \(X\) ,它的取值为 \(x_1,x_2,...,x_n\) ,其概率分别为 \(p(x_1),p(x_2),...,p(x_n)\) 。把 \(X\) 想象成我们在一个 机会游戏 (game of chance )中得到的奖金,也就是说,我们将赢得 \(x_i\) 单位奖金的概率为 \(p(x_i)\) 。根据概率的频率解释,如果我们继续玩这个游戏,那么我们赢得 \(x_i\) 的次数占比将是 \(p(x_i)\) 。因此,我们在 \(n\) 次比赛中的平均奖金将是:
\[
\sum_{i=1}^{n}{x_ip(x_i)} = E[X]
\tag{4.43}\]
为了更清楚地看到 式 4.43 所示的结论,假设我们玩 \(N\) 次游戏,其中 \(N\) 是一个非常大的数。在这些游戏中,我们将赢得 \(x_i\) 的次数大约为 \(Np(x_i)\) ,因此我们在 \(N\) 次比赛中的总奖金将是:
\[
\sum_{i=1}^{n}{x_i \cdot Np(x_i)}
\]
所以,我们可以获得的平均奖金为:
\[
\sum_{i=1}^{n}{\frac{x_i \cdot Np(x_i)}{N}} = \sum_{i=1}^{n}{x_ip(x_i)} = E[X]
\]
习题 4.8 随机变量 \(X\) 为我们抛一个骰子所获得的点数,计算 \(E[X]\) 。
解 4.8 . \[
\begin{align}
\because\ & p(1)=p(2)=p(3)=p(4)=p(5)=p(6)=\frac{1}{6} \\
\therefore\ & E[X] = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6} = \frac{7}{2}
\end{align}
\]
读者应该注意,在 习题 4.8 中,\(X\) 的期望值并不是 \(X\) 的可能取值(也就是说,抛一个骰子,我们不可能得到 的点数)。因此,即使我们称 \(E[X]\) 为 \(X\) 的期望,我们也不能应该把 \(E[X]\) 看作我们期望 \(X\) 具有的值,而应该看作在大量重复实验中 \(X\) 的平均值。也就是说,如果我们连续抛一个骰子,那么在抛了很多次之后,所得结果的平均点数将大约是 \(\frac{7}{2}\) 。(感兴趣的读者可以尝试一下这个实验。)\(\blacksquare\)
例 4.7 \(A\) 的 指示随机变量 为 \(I\) ,如果
\[
I = \begin{cases}
1, \quad & 如果 A 发生\\
0, \quad & 如果 A 不发生
\end{cases}
\]
则 \(E[I] = 1 \cdot P(A) + 0 \cdot P(A^c) = P(A)\) 。因此,指示随机变量 的期望就是对应的事件发生的概率。\(\blacksquare\)
例 4.8 熵(Entropy) 。给定一个 随机变量 \(X\) ,\(X=x\) 传递了多少信息(information )?让我们通过如下的方式来开始尝试量化 \(X=x\) 中所传递的信息:\(X=x\) 的信息量应该取决于 \(X\) 等于 \(x\) 的可能性。\(X\) 等于 \(x\) 的可能性越小,他所包含的信息就越多,这看起来是合理的。例如:如果 \(X\) 表示抛两个骰子的点数之和,则 \(X = 12\) 包含的信息量比 \(X = 7\) 包含的信息量要大(因为 \(P\{X=12\}=\frac{1}{36}\) ,而 \(P\{X=7\}=\frac{1}{6}\) )。
让我们用 \(I(p)\) 来表示一个概率为 \(p\) 的事件发生时的信息量。显然,\(I(p)\) 应该是 \(p\) 的非负递减函数。为了确定 \(I(p)\) ,令 \(X\) 和 \(Y\) 是独立 随机变量 ,假设 \(P\{X=x\}=p\) 、\(P\{Y=y\}=q\) 。那么 \(X=x\) 、\(Y=y\) 包含多少信息量?
首先,\(X=x\) 中包含的信息量是 \(I(p)\) 。
此外,由于我们已经知道 \(Y=y\) 的概率并不受 \(X=x\) 的影响(因为 \(X\) 和 \(Y\) 是独立的),所以 \(Y=y\) 中包含的额外信息量应该等于 $I(q)。
因此,\(X=x\) 、\(Y=y\) 中的信息量为 \(I(p)+I(q)\) 。
另一方面,我们有 \(P\{X=x, Y=y\}=P\{X=x\}P\{Y=y\}=pq\) ,这意味着 \(X=x\) 、\(Y=y\) 中的信息量为 \(I(pq)\) 。
因此,看起来,\(I\) 应该满足:\(I(pq) = I(p) + I(q)\) 。
如果我们定义函数 \(G\) 为:\(G(p)=I(2^{-p})\) ,于是有:
\[
\begin{align}
G(p+q) &= I(2^{-(p+q)}) \\
&= I(2^{-p} \cdot 2^{-q}) \\
&= I(2^{-p}) + I(2^{-q}) \\
&= G(p) + G(q)
\end{align}
\]
可以证明,满足上述关系的唯一的单调函数 \(G\) 是 \(G(p) = cp\) ,其中 \(c\) 为常数。
于是,我们有 \(I(2^{-p}) = cp\) ,令 \(q=2^{-p}\) ,则 \(I(q) = -c \log_2{q}\) (其中,\(c\) 是一个大于 0 的常数)。我们经常令 \(c=1\) ,并且说:用 位(bits ) 来测量信息量。
现在,考虑一个随机变量 \(X\) ,它的取值为 \(x_1,x_2,...,x_n\) ,其概率分别为 \(p_1,p_2,...,p_n\) 。因为 \(X=x\) 的信息量为 \(-\log_2(p_i)\) ,因此,\(X=x_i\) 所包含的信息量的 期望 为:
\[
H(X) = - \sum_{i=1}^{n}{p_i \log_2{p_i}}
\]
在信息论中,\(H(X)\) 就是众所周知的 随机变量 \(X\) 的 熵(entropy ) 。 \(\blacksquare\)
我们还可以定义连续 随机变量 的 期望 。假设 \(X\) 是一个概率密度函数为 \(f\) 的连续 随机变量 。对于一个较小的数 \(\Delta x\) ,有:
\[
f(x) \Delta x \approx P\{x \lt X \lt x + \Delta x\}
\]
如果 \(x\) 的权重等于 \(X\) 在 \(x\) 附近的概率,则 \(X\) 的所有可能值的加权平均数就是 \(xf(x) \Delta x\) 在所有 \(x\) 上的积分。通常,定义 \(X\) 的期望为:
\[
E[X] = \int_{-\infty}^{\infty}{xf(x) \mathrm{d} x}
\]
例 4.9 \(X\) 个小时内会收到消息,并且 \(X\) 是一个 随机变量 ,其概率密度函数为:
\[
f(x) = \begin{cases}
\frac{1}{1.5}, \quad & 0 \lt x \lt 1.5 \\
0, \quad & otherwise
\end{cases}
\]
则下午 5 点之后可以收到消息的期望时间为:\(E[X] = \int_{0}^{1.5}{\frac{1}{1.5} \mathrm{d} x} = 0.75\) 。因此,您等待消息的时间平均为 45 分钟。 \(\blacksquare\)
期望 的概念类似于物理中的 重心 的概念。考虑一个离散 随机变量 \(X\) ,其概率质量函数为 \(p(x_i), i \ge 1\) 。如果我们现在想象一个质量可以忽略不计的杆(weightless rod ),在这根杆上的 \(x_i\) 处的质量为 \(p(x_i)\) (\(i \ge 1\) )(见 图 4.4 )。那么这根杆处于平衡状态的点称为重心(the center fo gravity )。对于那些熟悉统计学基础的读者来说,很容易证明这根杆的重心位于 \(E[X]\) 。
\(E[X]\) 的计量单位与 \(X\) 相同。
期望的特征
假设我们给定一个 随机变量 \(X\) 和其 概率分布 。又假设,我们对计算 \(X\) 的 期望 不感兴趣,而对计算关于 \(X\) 的某个函数 \(g(X)\) 的 期望 感兴趣。如何计算 \(g(X)\) 的 期望 ?如下就是一种计算方法。由于 \(g(X)\) 本身是一个 随机变量 ,因此 \(g(X)\) 必存在一个概率分布,并且这个概率分布可以通过 \(X\) 的概率分布来计算。一旦我们得到了 \(g(X)\) 的分布,我们就可以通过期望的定义来计算 \(E[g(X)]\) 。
概率分布即——离散 随机变量 的 概率质量函数 或连续 随机变量 的 概率密度函数 。
习题 4.9 \(X\) 的概率质量函数函数为:\(p(0)=0.2\) ,\(p(1)=0.5\) ,\(p(2)=0.3\) ,计算 \(E[X^2]\) 。
解 4.9 . \(Y=X^2\) ,则 \(Y\) 是一个取值为 \(0^2\) ,\(1^2\) ,\(2^2\) 的 随机变量 ,并且其可能取值的概率分别为:
\(p_Y(0) = P\{Y = 0^2\} = 0.2\)
\(p_Y(1) = P\{Y = 1^2\} = 0.5\)
\(p_Y(2) = P\{Y = 2^2\} = 0.3\)
因此,\(E[X^2] = E[Y] = 0 \cdot 0.2 + 1 \cdot 0.5 + 4 \cdot 0.3 = 1.7\) 。\(\blacksquare\)
习题 4.10 随机变量 \(X\) ,其概率密度函数为:
\[
f_X(x) = \begin{cases}
1, \quad & 0 \lt x \lt 1 \\
0, \quad & otherwise
\end{cases}
\]
如果对修复时间 \(x\) 的细分成本是 \(x^3\) ,那么这种细分的期望成本是多少?
解 4.10 . \(Y = X^3\) ,我们首先计算 \(Y\) 的分布函数:
\[
\begin{align}
F_Y(a) &= P\{Y \le a\} \\
&= P\{X^3 \le a\} \\
&= P\{X \le a^{\frac{1}{3}}\} \\
&= \int_{0}^{a^{\frac{1}{3}}}{1 \mathrm{d} x} \\
&= a^{\frac{1}{3}} \\
其中,& 0 \le a \le 1
\end{align}
\]
对 \(F_Y(a)\) 求导得到概率密度函数 \(f_Y(a)=\frac{1}{3}a^{-\frac{2}{3}},\ 0 \le a \le 1\) 。因此:
\[
\begin{align}
E[X^3] &= E[Y] = \int_{-\infty}^{\infty}{a \cdot f_Y(a) da} \\
&= \int_{0}^{1}{a \cdot a^{-\frac{2}{3}} da} \\
&= \frac{1}{3} \int_{0}^{1}{a^{\frac{1}{3}}da} \\
&= (\frac{1}{3} \cdot \frac{3}{4} \cdot a^{\frac{4}{3}}) \big |_{0}^{1} \\
&= \frac{1}{4} \quad \blacksquare
\end{align}
\]
虽然上述过程允许我们可以在理论上利用 \(X\) 的分布来计算 \(X\) 的任何函数的 期望 ,但我们还有一种更简单的方法。例如,假设我们想计算 \(g(X)\) 的 期望 。当 \(X=x\) 时,\(g(X)\) 的取值为 $g(x),因此 \(E[g(X)]\) 应该是 \(g(X)\) 的加权平均数,其中 \(g(x)\) 的权重就是 \(X=x\) 的概率(或概率密度)。事实上,我们可以证明上述过程是正确的,因此我们有以下的命题。
命题 4.1 随机变量 的函数的 期望 :
如果一个离散 随机变量 \(X\) 的概率质量函数为 \(p(x)\) ,则对于任一函数 \(g\) ,\(E[g(X)] = \sum_{x}{g(x)p(x)}\) 。
如果一个连续 随机变量 \(X\) 的概率密度函数为 \(f(x)\) ,则对于任一函数 \(g\) ,\(E[g(X)] = \int_{-\infty}^{\infty}{g(x)f(x) \mathrm{d} x}\) 。
例 4.10 命题 4.1 来计算 习题 4.9 有:
\(E[X^2] = 0^2 \cdot 0.2 + 1^2 \cdot 0.5 + 2^2 \cdot 0.3 = 1.7\) 。\(\blacksquare\)
例 4.11 命题 4.1 来计算 习题 4.10 有:
\(E[X^3] = \int_{0}^{1}{x^3} \mathrm{d} x = \frac{1}{4}\) 。 \(\blacksquare\)
根据 命题 4.1 ,我们有 推论 4.1 。
推论 4.1 \(a\) 和 \(b\) 是常数,则 \(E[aX + b] = aE[X] + b\) 。
证 .
对于离散随机变量: \[
\begin{align}
E[aX + b] &= \sum_{x}{(ax + b)p(x)} \\
&= a\sum_{x}{xp(x)} + b\sum_{x}{p(x)} \\
&= aE[X] + b
\end{align}
\]
对于连续随机变量: \[
\begin{align}
E[aX + b] &= \int_{-\infty}^{\infty}{(ax + b)f(x) \mathrm{d} x} \\
&= a\int_{-\infty}^{\infty}{xf(x) \mathrm{d} x} + b\int_{-\infty}^{\infty}{f(x) \mathrm{d} x} \\
&= aE[X] + b \quad \blacksquare
\end{align}
\]
如果令 \(a=0\) ,则根据 推论 4.1 有:\(E[b] = b\) 。也就是说,常量的 期望 就是它本身。(这符合你的直觉吗?)另外,如果我们令 \(b=0\) ,那么我们得到 \(E[aX] = aE[X]\) 。
换句话说,常数乘以 随机变量 的 期望 就是该常数乘以这个 随机变量 的期望。随机变量 \(X\) 的 期望 \(E[X]\) 也称为 \(X\) 的平均值或一阶矩(the first moment )。当 \(n \ge 1\) 时,\(E[X^n]\) 称为 \(X\) 的 \(n\) -阶矩。根据 命题 4.1 ,我们有:
\[
E[X^n] = \begin{cases}
\sum_{x}{x^np(x)}, \quad & X 为离散随机变量\\
& \\
& \\
\int_{-\infty}^{\infty}{x^nf(x) \mathrm{d} x}, \quad & X 为连续随机变量
\end{cases}
\]
随机变量和的期望
对于 命题 4.1 而言,如果有两个 随机变量 \(X\) 、\(Y\) ,并且 \(g\) 为关于 \(X\) 、\(Y\) 的函数,那么有:
\[
E[g(X,Y)] = \begin{cases}
\sum_{y} \sum_{x} g(x,y)p(x,y), \quad & 离散随机变量\\
& \\
& \\
\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)f(x,y) \mathrm{d} x \mathrm{d} y, \quad & 连续随机变量
\end{cases}
\]
例如,如果 \(g(X,Y)=X+Y\) 且 \(X\) 、\(Y\) 为连续 随机变量 ,则:
\[
\begin{align}
E[X+Y] &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(x+y)f(x,y) \mathrm{d} x \mathrm{d} y \\
&= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf(x,y) \mathrm{d} x \mathrm{d} y + \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}yf(x,y) \mathrm{d} x \mathrm{d} y \\
&= E[X] + E[Y]
\end{align}
\]
类似的,对于离散随机变量而言,也有:
\[
E[X+Y]=E[X] + E[Y]
\tag{4.44}\]
重复应用 式 4.44 ,我们可以证明:任意数量的 随机变量 之和的 期望 等于它们各自 期望 的和。例如,
\[
\begin{align}
E[X+Y+Z] &= E[(X+Y)+Z] \\
&= E[X+Y] + E[Z] \\
&= E[X] + E[Y] + E[Z]
\end{align}
\]
更一般的,对于任意的 \(n\) ,
\[
E[X_1 + X_2 + ... + X_n] = E[X_1] + E[X_2] + ... + E[X_n]
\tag{4.45}\]
式 4.45 是一个非常有用的公式,接下来,我们将通过一系列的例子来说明其作用。
习题 4.11
解 4.11 . \(X\) 是两个骰子的和,则
\(E[X]=\sum_{i=2}^{12}{iP\{X=i\}}\)
我们令 \(X_1\) 、\(X_2\) 分别表示这两个骰子的点数,则有 \(X = X_1 + X_2\) ,于是有:
\(E[X] = E[X_1 + X_2] = E[X_1] + E[X_2]\) ,根据 式 4.45 有 \(E[X] = 7\) 。\(\blacksquare\)
习题 4.12
解 4.12 . \(X_i\) 表示投标的第 \(i\) 个项目的利润,其中 \(i=1,2,3\) 。令 \(X\) 表示总利润,则 \(X = X_1 + X_2 + X_3\) 。所以,
\(E[X] = E[X_1 + X_2 + X_3] = E[X_1] + E[X_2] + E[X_3] = 3 万美元\) 。\(\blacksquare\)
习题 4.13 \(N\) 封信件以及信件对应的信封。当信封掉在地板上时,他们会混在一起。如果这 \(N\) 封信件以完全随机的方式放在已经混淆的信封里(每封信件放在任何一个信封的概率相同),则放到正确的信封中的信件数量的期望值是多少?
解 4.13 . \(X\) 表示放到正确的信封中的信件数量,则:
\(X = X_1 + X_2 + ... + X_N\) ,其中 \(X_i = \begin{cases} 1, \quad & 第 i 封信放在了第 i 个信封中\\ 0, \quad & 其他 \end{cases}\) 。
由于第 \(i\) 封信放入 \(N\) 个信封中的可能性是相同的,因此,\(P\{X_i=1\}=\frac{1}{N}\) 。
所以有:\(E[X_i]=1 \cdot P\{X_i = 1\} + 0 \cdot P\{X_i = 0\} = \frac{1}{N}\) ,根据 式 4.45 有:
\(E[X] = E[X_1] + ... + E[X_N] = \frac{1}{N} N =1\) 。
因此,不管有多少封信,平均来说,只有一封信会放在正确的信封里。\(\blacksquare\)
习题 4.14
解 4.14 . \(X\) 表示这 10 张优惠券中包含的优惠券类型的数量,则:
\(X = X_1 + ... + X_20\) ,其中 \(X_i = \begin{cases} 1, \quad & 至少有 1 张第 i 种优惠券\\ 0, \quad & 其他 \end{cases}\) 。
所以有:
\[
\begin{align}
E[X_i] &= P\{X_i = 1\} \\
&= P\{在 10 张优惠券中至少有 1 张第 i 种优惠券\} \\
&= 1 - P\{在 10 张优惠券中不存在第 i 种优惠券\} \\
&= 1 - \bigg(\frac{19}{20}\bigg)^{10}
\end{align}
\]
所以 \(E[X] = E[X_1] + ... + E[X_20] = 20 \cdot \Bigg(1 - \big(\frac{19}{20}\big)^{10}\Bigg) = 8.025\) 。\(\blacksquare\)
当我们必须预测一个 随机变量 的值时,均值(mean )的一个重要属性就显现出来了。也就是说,假设要预测一个 随机变量 \(X\) 的值,如果我们预测 \(X\) 将等于 \(c\) ,那么预测“误差”(或者称为:残差)的平方将是 \((X−c)^2\) 。接下来,我们将证明:当 \(X\) 的预测值等于它的均值 \(\mu\) 时,均方误差的值是最小的。
对于任何常数 \(c\) 有:
\[
\begin{align}
E[(X-c)^2] &= E[(X - \mu + \mu - c)^2] \\
&= E[(X - \mu)^2 + 2(X - \mu)(\mu - c) + (\mu -c)^2] \\
&= E[(X - \mu)^2] + 2(\mu - c)E[(X - \mu)] + (\mu -c)^2 \\
&= E[(X - \mu)^2] + (\mu -c)^2, \qquad \because E[X - \mu] = E[X] - \mu = 0 \\
&\ge E[(X - \mu)^2]
\end{align}
\tag{4.46}\]
因此,当 随机变量 的平方误差的期望最小时,可以得到 随机变量 的最佳预测器——即其平均值。
方差
给定一个 随机变量 \(X\) 及其概率分布函数,如果我们能够定义某些合适的度量并用来总结质量函数的基本特征,那将是非常有用的。期望 \(E[X]\) 就是其中的一个度量。虽然 \(E[X]\) 生成了 \(X\) 的可能值的加权平均数,但 \(E[X]\) 却没有告诉我们 \(X\) 的这些可能值的变化。例如,当 随机变量 \(W\) 、\(Y\) 、\(Z\) 的概率质量函数分别为:
\(W=0 \quad 概率为 1\)
\(Y=\begin{cases} -1, \quad & 概率为 \frac{1}{2}\\ 1, \quad & 概率为 \frac{1}{2} \end{cases}\)
\(Y=\begin{cases} -100, \quad & 概率为 \frac{1}{2}\\ 100, \quad & 概率为 \frac{1}{2} \end{cases}\)
虽然这三个 随机变量 的期望都是 0,但是 \(Y\) 的变化幅度比 \(W\) 要大,同时 \(Z\) 的变化幅度比 \(Y\) 也要大。
因为我们期望 \(X\) 在其平均值 \(E[X]\) 附近取值,所以可以利用 \(X\) 的实际取值与 \(E[X]\) 之间的距离来测量 \(X\) 的变化。可以同过量化 \(E[|X − \mu|]\) 来计算 \(X\) 的实际取值与 \(E[X]\) 之间的距离,其中 \(\mu = E[X]\) ,\(|X − \mu|\) 代表 \(X - \mu\) 的绝对值。然而,事实证明,在数学上处理 \(E[|X − \mu|]\) 极其麻烦。因此,我们通常会用一个更容易处理的数据——即 \(X\) 与其平均值之差的平方的期望。
定义 4.1 \(X\) 是一个均值为 \(\mu\) 的 随机变量 ,则 \(X\) 的 方差 (variance )\(\textup{Var}(X)\) 为:\(\textup{Var}(X) = E[(X - \mu)^2]\) 。
于是,我们有如下的推导:
\[
\begin{align}
\textup{Var}(X) &= E[(X - \mu)^2] \\
&= E[X^2 - 2 \mu X + \mu ^2] \\
&= E[X^2] - 2 \mu E[X] + \mu ^2 \\
&= E[X^2] - (E[X])^2 \quad \because E[X] = \mu \\
\end{align}
\]
所以有:
\[
\textup{Var}(X) = E[X^2] - (E[X])^2
\tag{4.47}\]
换句话说,\(X\) 的方差等于 \(X\) 的平方的期望减去 \(X\) 的期望的平方。实际上,通常,式 4.47 是计算 \(\textup{Var}(X)\) 的最简单的方法。
习题 4.15 \(X\) 为抛一个骰子的点数,计算 \(\textup{Var}(X)\) 。
解 4.15 . \(P\{X=i\}=\frac{1}{6}\) ,\(i=1,2,...,6\) ,因此:
\(E[X^2] = \sum_{i=1}^{6}{i^2 \cdot P\{X=i\}} = \frac{91}{6}\) 。
在 习题 4.8 中,我们知道 \(E[X]=\frac{7}{2}\) ,根据 式 4.47 :
\(\textup{Var}(X)=E[X^2] - (E[X])^2 = \frac{91}{6} - (\frac{7}{2})^2 = \frac{35}{12}\) 。\(\blacksquare\)
例 4.12 指示随机变量的方差 ,对于事件 \(A\) ,指示随机变量 \(I\) 为:
\(I = \begin{cases} 1, \quad & 如果 A 发生\\ 0, \quad & 如果 A 不发生 \end{cases}\)
根据 例 4.7 有,\(E[I] = P(A)\) ,所以有: \[
\begin{align}
\textup{Var}(I) &= E[I^2] - (E(I))^2 \\
&= E[I] - (E[I])^2 \quad \because I^2=I \\
&= E[I](1-E[I]) \\
&= P(A)(1-P(A)) \qquad \blacksquare
\end{align}
\]
因为 \((X - \mu)^2 \ge 0\) ,因此,\(\textup{Var}(X) = E[(X - \mu)^2] \ge 0\) ,根据 式 4.47 有:
\[
E[X^2] \ge \mu^2
\tag{4.48}\]
也就是说,一个 随机变量 的平方的 期望 至少与其 期望 的平方一样大。
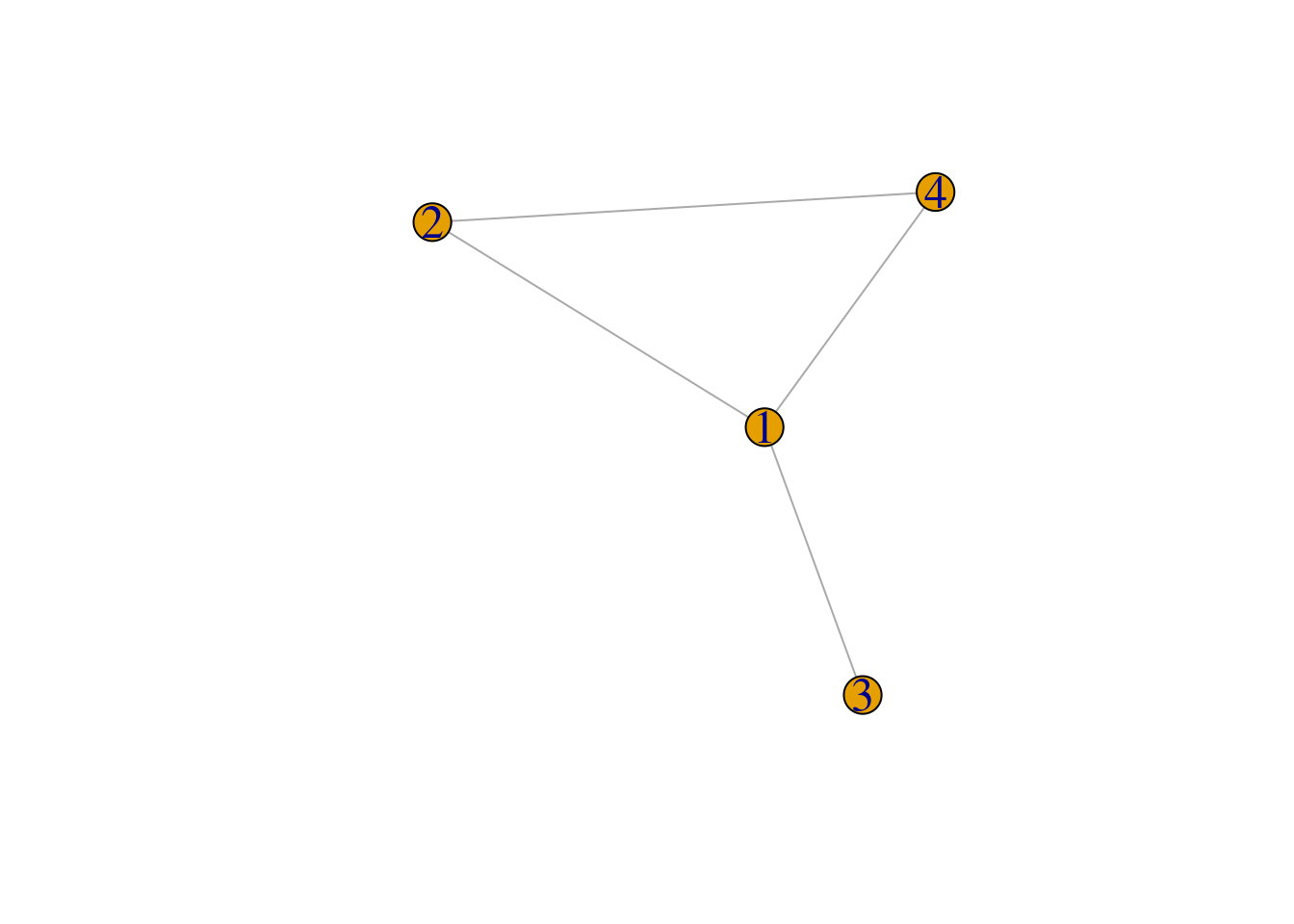
例 4.13 友谊悖论 (friendship paradox )表明:平均而言,你的朋友的朋友数量比你的朋友数量要更多。更正式地,假设某个人群中有 \(n\) 个人,标记为 \(1,2,...,n\) ,这些人中的某些人之间是朋友。这个 朋友网络 (friendship network )可以用 图 (graphic )来表示:用顶点表示每个人,然后用顶点与顶点之间的连线表示这些人是朋友。例如,如 图 4.5 所示,该社区中有 4 个人,第 1 个人和第 2 个人是朋友,第 1 个人和第 3 个人是朋友,第 1 个人和第 4 个人是朋友,第 2 个人和第 4 个人是朋友。
代码
library (igraph)<- c (1 , 2 , 3 , 4 ) <- cbind (c (1 , 1 , 1 , 2 ), c (3 , 2 , 4 , 4 )) <- graph_from_edgelist (edges, directed = FALSE ) V (g)$ label <- verticesplot (g, vertex.label.cex = 1.5 )
令 \(f(i)\) 表示第 \(i\) 个人的朋友数,令 \(f=\sum_{i=1}^{n}{f(i)}\) 。在 图 4.5 中,\(f(1)=3\) ,\(f(2)=2\) ,\(f(3)=1\) ,\(f(4)=2\) ,\(f = 8\) 。
我们随机选择一个人,并用 \(X\) 表示,\(X\) 可以是 \(1,2,...,n\) 中的任何一个,并且选取到的概率是一致的。也就是说,
\(P(X=i)=\frac{1}{n}\)
根据 命题 4.1 ,\(X\) 的朋友数量的期望 \(E[f(X)]\) 为:
\(E[f(X)] = \sum_{i=1}^{n}{f(i)P(X=i)}=\sum_{i=1}^{n}{\frac{f(i)}{n}} = \frac{f}{n}\)
假设这 \(n\) 个人中的每个人都将他所有朋友的名字分别写在了一张单独的纸上(一个名字一张纸)。因此,一个有 \(k\) 个朋友的人将使用 \(k\) 张纸。因为第 \(i\) 个人有 \(f(i)\) 个朋友,因此总共会有 \(\sum_{i=1}^{n{f(i)}}\) 张纸来记录名字。
现在随机选择一张纸,令 \(Y\) 表示纸上的名字,并计算所选纸上的人的朋友数量的期望 \(E[f(Y)]\) 。
首先,因为第 \(i\) 个人有 \(f(i)\) 个朋友, 所以有 \(f(i)\) 张纸上的名字写的是 \(i\) ,因此,所选择的纸上的名字为 \(i\) 的概率为 \(\frac{f(i)}{f}\) ,即:
\(P(Y=i)=\frac{f(i)}{f}, i = 1,...,n\)
于是,\(E[f(Y)] = \sum_{i=1}^{n}{f(i)P(Y=i)} = \frac{\sum_{i=1}^{n}{f^2(i)}}{f}\) 。
因为 \(P(X=i)=\frac{1}{n}\) ,\(E[f(X)] = \frac{f}{n}\) ,所以 \(f = \frac{E[f(x)]}{P(X=i)}\) ,所以有:
\[
\begin{align}
E[f(Y)] &= \frac{\sum_{i=1}^{n}{f^2(i)}}{f} \\
&= \frac{\sum_{i=1}^{n}{f^2(i)P(X=i)}}{E[f(X)]} \\
&= \frac{E[f^2(X)]}{E[f(X)]} \\
&\ge E[f(X)], \ \because E[X^2] \ge \mu^2
\end{align}
\]
因此,\(E[f(X)] \le E[f(Y)]\) ,这表明随机选择的某个人的平均朋友数量小于或等于其朋友的平均朋友数量。
从直觉上讲,友谊悖论的原因在于:
选择 \(X\) 的概率是相同的(\(X\) 为 \(n\) 个人中的任何一个的概率是相同)。
选择 \(Y\) 的概率与其朋友数量成正比。
所以,一个人拥有的朋友越多,这个人就越有可能是 \(Y\) 。因此,\(Y\) 偏向于拥有大量朋友的那个人。
因此,\(Y\) 拥有的平均朋友数量大于 \(X\) 拥有的平均朋友数量也就不足为奇了。
“友谊悖论”(friendship paradox)这一现象由社会学家斯科特·费尔德(Scott L. Feld)于1991年发现,其原因在于,那些在社交网络中连接较为广泛的人(即拥有较多朋友的人)更容易被其他人选为朋友,从而使得在统计上呈现出这样看似矛盾的结果。
\(\blacksquare\)
对于任意的常数 \(a\) 、\(b\) ,有:
\[
\textup{Var}(aX + b) = a^2 \textup{Var}(X)
\tag{4.49}\]
证 . \(\mu = E[X]\) ,根据 推论 4.1 有 \(E[aX + b] = a \mu + b\) ,根据方差的定义 定义 4.1 有:
\[
\begin{align}
\textup{Var}(aX + b) &= E[(aX + b - E[aX + b])^2] \\
&= E[(aX + b - a \mu - b)^2] \\
&= E[(aX - a \mu)^2] \\
&= E[a^2(X - \mu)^2] \\
&= a^2E[(X - \mu)^2] \\
&= a^2\textup{Var}(X)
\end{align}
\]
式 4.49 中,对于特定的 \(a\) 和 \(b\) 可以导出其他的推论。例如,如果 \(a=0\) ,则有:
\(\textup{Var}(b) = 0\)
即:常数的方差为 0(这符合直觉吗?)。类似的,令 \(a = 1\) ,则有:
\(\textup{Var}(X + b) = \textup{Var}(X)\)
也就是说,随机变量 加一个常数的方差等于该 随机变量 的方差。最后,令 \(b=0\) ,则有:
\(\textup{Var}(aX) = a^2\textup{Var}(X)\)
\(\sqrt{\textup{Var}(X)}\) 称为 \(X\) 的标准差(standard deviation )。随机变量 的标准差和均值具有相同的单位。
与 均值 是质量分布的 重心 的概念类似,在力学中,方差 代表 惯性矩 (the moment of inertia )。
在力学中,惯性矩(又称转动惯量)是一个用于描述物体绕轴转动时惯性大小的物理量。
具体来说,它衡量了物体对于绕某一特定轴转动的抵抗能力。惯性矩越大,物体绕该轴转动就越困难,也就越不容易改变其转动状态;反之,惯性矩越小,物体就相对更容易改变其转动状态。
其数学定义通常是对于质量分布为 \(m_i\) 、距离转动轴为 \(r_i\) 的多个质点组成的物体,惯性矩等于各质点质量与该质点到转动轴距离平方的乘积之和,即 \(I=\sum m_ir_i^2\) 。
例如,对于一个均匀圆盘,其绕中心轴的惯性矩与圆盘的质量和半径的平方有关;对于一个细长的直杆,绕垂直于杆且通过一端的轴转动时,其惯性矩也有特定的表达式。惯性矩在研究物体的转动运动、机械设计等方面都有着重要的应用。
方差和惯性矩有一定的相似性,但不能简单地说方差就是惯性矩。方差主要是用来描述一组数据离散程度的统计量。它反映了数据相对于均值的偏离程度。而惯性矩是在力学中用于衡量物体绕轴转动时惯性大小的物理量。
从某种意义上来说,它们有一些相似之处。比如两者都涉及到对“差异”或“偏离”的一种度量。在惯性矩中,是质量分布相对于转动轴的偏离程度;在方差中,是数据点相对于均值的偏离程度。
协方差以及随机变量的和的方差
在 小节 4.5 随机变量 之和的 期望 等于它们各自 期望 的和(式 4.45 )。但是,对于 方差 而言,却并非如此。例如:
\[
\begin{align}
Var(X+X) &= Var(2X) \\
&= 2^2 Var(X) \\
&= 4 Var(X) \\
& \ne Var(X) + Var(X)
\end{align}
\]
然而,当这些 随机变量 是独立的条件时,随机变量 的和的 方差 等于这些 随机变量 各自的方差的和。但是,在证明这一点之前,我们先定义两个 随机变量 的 协方差 (covariance ) 的概念。
定义 4.2 随机变量 \(X\) 、\(Y\) 的 协方差 \(\textup{Cov}(X,Y)\) 的定义如下:
\(\textup{Cov}(X,Y) = E[(X - \mu_x)(Y - \mu_y)]\) ,其中 \(\mu_x\) 和 \(\mu_y\) 分别为 \(X\) 和 \(Y\) 的均值。
对 定义 4.2 中的等式右边进行展开,则有:
\[
\begin{align}
\textup{Cov}(X,Y) &= E[XY - \mu_x Y -\mu_y X + \mu_x \mu_y] \\
&= E[X,Y] - \mu_xE[Y] - \mu_yE[X] + \mu_x \mu_y \\
&= E[XY] - \mu_x \mu_y - \mu_y \mu_x + \mu_x \mu_y \\
&= E[XY] - E[X]E[Y]
\end{align}
\tag{4.50}\]
根据 定义 4.2 ,我们可以知道 协方差 满足如下的性质:
\[
\textup{Cov}(X,Y) = \textup{Cov}(Y,X)
\tag{4.51}\]
\[
\textup{Cov}(X,X) = \textup{Var}(X)
\tag{4.52}\]
\[
\textup{Cov}(aX, Y) = a \textup{Cov}(X, Y)
\tag{4.53}\]
与 期望 一样,协方差 也具有加和性(additive property )。
引理 4.1 \(\textup{Cov}(X_1 + X_2, Y) = \textup{Cov}(X_1, Y) + \textup{Cov}(X_2,Y)\)
证 . \[
\begin{align}
\textup{Cov}(X_1 + X_2,Y) &= E[(X_1+X_2)Y] - E[X_1+X_2]E[Y] \\
&= E[X_1Y] + E[X_2Y]-(E[X_1] + E[X_2])E[Y] \\
&= E[X_1Y] - E[X_1]E[Y] + E[X_2Y] - E[X_2]E[Y] \\
&= \textup{Cov}(X_1,Y) + \textup{Cov}(X_2,Y) \quad \blacksquare
\end{align}
\]
引理 4.1 的一般形式如下:
\[
\textup{Cov}\bigg( \sum_{i=1}^{n}{X_i},Y \bigg) = \sum_{i=1}^{n}{\textup{Cov}(X_i,Y)}
\tag{4.54}\]
命题 4.2 \[
\textup{Cov}\bigg( \sum_{i=1}^{n}{X_i},\sum_{j=1}^{m}{Y_j} \bigg) = \sum_{i=1}^{n} \sum_{j=1}^{m} {\textup{Cov}(X_i,Y_j)}
\]
证 . \[
\begin{align}
\textup{Cov}\bigg( \sum_{i=1}^{n}{X_i},\sum_{j=1}^{m}{Y_j} \bigg) &= \sum_{i=1}^{n}{\textup{Cov}\bigg(X_i, \sum_{j=1}^{m}{Y_j}\bigg)} \\
&= \sum_{i=1}^{n}{\textup{Cov}\bigg(\sum_{j=1}^{m}{Y_j}, X_i\bigg)} \\
&= \sum_{i=1}^{n} \sum_{j=1}^{m} {\textup{Cov}(Y_j,X_i)} \\
&= \sum_{i=1}^{n} \sum_{j=1}^{m} {\textup{Cov}(X_i,Y_j)} \quad \blacksquare
\end{align}
\]
使用 式 4.52 可以得到 随机变量 之和的方差的公式。
推论 4.2 \[
\textup{Var}\bigg( \sum_{i=1}^{n}{X_i} \bigg) = \sum_{i=1}^{n}{\textup{Var}(X_i)} + \sum_{i=1}^{n} \sum_{\begin{align} &j=1 \\ &j \ne i \end{align}}^{n} {\textup{Cov}(X_i, X_j)}
\]
证 . \(\textup{Cov}(X, X) = \textup{Var}(X)\) (式 4.52 ),根据 命题 4.2 有:
\[
\begin{align}
\textup{Var}\bigg( \sum_{i=1}^{n}{X_i} \bigg) &= \textup{Cov}\bigg( \sum_{i=1}^{n}{X_i}, \sum_{j=1}^{n}{X_j} \bigg) \\
&= \sum_{i=1}^{n} \sum_{j=1}^{n} {\textup{Cov}(X_i, X_j)} \\
&= \sum_{i=1}^{n} \bigg( \sum_{j \ne i}{\textup{Cov}(X_i, X_j)} + \textup{Cov}(X_i, X_i)\bigg) \\
&= \sum_{i=1}^{n} \sum_{j \ne i} {\textup{Cov}(X_i, X_j)} + \sum_{i=1}^{n}{\textup{Cov}(X_i, X_i)} \\
&= \sum_{i=1}^{n} \sum_{j \ne i} {\textup{Cov}(X_i, X_j)} + \sum_{i=1}^{n}{\textup{Var}(X_i)} \quad \blacksquare
\end{align}
\]
当 \(n = 2\) 时,推论 4.2 变为:
\(\textup{Var}(X+Y) = \textup{Var}(X) + \textup{Var}(Y) + \textup{Cov}(X,Y) + \textup{Cov}(Y,X)\)
根据 式 4.51 有:
\[
\textup{Var}(X+Y) = \textup{Var}(X) + \textup{Var}(Y) + 2\textup{Cov}(X,Y)
\tag{4.55}\]
定理 4.1 \(X\) 和 \(Y\) 是独立 随机变量 ,则 \(\textup{Cov}(X,Y) = 0\) 。
更一般的,如果 \(X_1,...,X_n\) 是相互独立的 随机变量 ,则 \(\textup{Var}\bigg( \sum_{i=1}^{n}{X_i} \bigg)=\sum_{i=1}^{n}{\textup{Var}(X_i)}\) 。
证 . \(\textup{Cov}(X,Y) = 0\) ,根据 式 4.50 可知,我们需要证明:
\(E[XY] = E[X]E[Y]\)
如果 \(X\) 、\(Y\) 为独立离散随机变量,则有:
\[
\begin{align}
E[XY] &= \sum_{j}^{} \sum_{i}^{} {x_i y_i P\{X=x_i, Y=y_j\}} \\
&= \sum_{j}^{} \sum_{i}^{} {x_i y_i P\{X=x_i\}P\{Y=y_j\}} \quad \because X,Y 相互独立 \\
&= \sum_{y}^{}{y_jP\{Y=y_j\}} \cdot \sum_{j}^{}{x_iP\{X=x_i\}} \\
&= E[Y]E[X]
\end{align}
\]
故而有 \(\textup{Cov}(X,Y)=E[XY] - E[X]E[Y] = 0\) 。对于连续随机变量而言,该等式依然成立。所以 定理 4.1 得证。
习题 4.16 方差 。
解 4.16 . \(X_i\) 表示第 \(i\) 次的点数,则根据 习题 4.15 有,\(\textup{Var}(X_i) = \frac{35}{12}\) ,所以: \[
\begin{align}
\textup{Var}\bigg( \sum_{i=1}^{10}{X_i} \bigg) &= \sum_{i=1}^{10}{\textup{Var}(X_i)} \\
&= 10 \frac{35}{12} \\
&= \frac{175}{6} \quad \blacksquare
\end{align}
\]
习题 4.17 方差 。
解 4.17 . \(I_j = \begin{cases} 1, \quad & 第 j 次结果为正面向上\\ 0, \quad & 第 j 次结果为反面向上 \end{cases}\) ,
则 正面向上的总次数为 \(\sum_{j=1}^{10}{I_j}\) 。
根据 定理 4.1 有:\(\textup{Var}\bigg( \sum_{j=1}^{10}{I_j} \bigg) = \sum_{j=1}^{10}{\textup{Var}(I_j)}\) 。
现在,由于 \(I_j\) 是概率为 的 事件 的指示 随机变量 ,从 例 4.12 可知:
\(\textup{Var}(I_j) = \frac{1}{2}(1-\frac{1}{2}) = \frac{1}{4}\) ,因此:
\(\textup{Var}\bigg( \sum_{j=1}^{10}{I_j} \bigg) = \frac{10}{4}\) 。\(\blacksquare\)
两个 随机变量 的 协方差 可以作为一个重要指标以衡量它们之间的关系。例如,考虑 \(X\) 和 \(Y\) 是 事件 \(A\) 和 事件 \(B\) 是否发生的指标随机变量,即:
\(X = \begin{cases} 1, \quad & 如果 A 发生\\ & \\ 0, \quad & 如果 A 不发生 \end{cases}, \quad Y = \begin{cases} 1, \quad & 如果 B 发生\\ & \\ 0, \quad & 如果 B 不发生 \end{cases}\)
并且:
\(XY = \begin{cases} 1, \quad & 如果 X=1, Y=1\\ & \\ 0, \quad & 其他 \end{cases}\)
因此:
\(\begin{align} \textup{Cov}(X,Y) &= E[XY] - E[X]E[Y] \\ &= P\{X=1,Y=1\} - P\{X=1\}P\{Y=1\} \end{align}\)
故而:
\(\begin{align} \textup{Cov}(X,Y) \gt 0 & \Leftrightarrow P\{X=1,Y=1\} \gt P\{X=1\}P\{Y=1\} \\ & \Leftrightarrow \frac{P \{X=1,Y=1\}}{P\{X=1\}} \gt P\{Y=1\} \\ & \Leftrightarrow P\{Y=1|X=1\} \gt P\{Y=1\} \end{align}\)
如果 \(X=1\) 时,\(Y=1\) 的可能性更小,而 \(Y=0\) 的可能性更大,则 \(\textup{Cov}(X,Y) \lt 0\) 。(根据 协方差 的交换律,当 \(X\) 和 \(Y\) 互换时,如上的内容仍然正确。)
一般来说,\(\textup{Cov}(X,Y) \gt 0\) 表明 \(Y\) 会随着 \(X\) 的增加而增加,而 \(\textup{Cov}(X,Y) \lt 0\) 表明 \(Y\) 会随着 \(X\) 的增加而减少。可以用 \(X\) 和 \(Y\) 之间的相关性来表示 \(X\) 和 \(Y\) 之间关系的强度。\(X\) 和 \(Y\) 之间的相关性是其 协方差 除以其各自 标准差 的乘积得到的 无量纲量 (dimensionless )。即:
\[
\textup{Corr}(X,Y) = \frac{\textup{Cov}(X,Y)}{\sqrt{\textup{Var}(X) \textup{Var}(Y)}}
\tag{4.56}\]
可以证明,\(\textup{Corr}(X,Y)\) 的值总是介于 −1 和 +1 之间。
矩生成函数
矩生成函数(Moment Generating Function )是概率论中的一个重要概念,主要用于描述 随机变量 的概率分布。矩生成函数是 随机变量 的特征函数,我们可以利用矩生成函数得到 随机变量 的所有矩(平均值、方差、偏度等统计量)。
随机变量 \(X\) 的矩生成函数 \(\phi(t)\) 的定义如下:
\[
\phi(t) = E[e^{tX}] = \begin{cases}
\sum_{x}{e^{tx}p(x)}, \quad & 如果 X 为离散随机变量 \\
& \\
& \\
\int_{-\infty}^{\infty}{e^{tx}f(x) \mathrm{d} x}, \quad & 如果 X 为连续随机变量 \\
\end{cases}
\tag{4.57}\]
因为 \(X\) 的所有的矩都可以通过对 \(\phi(t)\) 求 \(k\) 阶导数来获得,因此我们称 \(\phi(t)\) 为矩生成函数。例如
\[
\begin{align}
\phi'(t) &= \frac{\mathrm{d} {E[e^{tX}]}}{\mathrm{d} t} \\
&= E\bigg[ \frac{\mathrm{d} {e^{tX}}}{\mathrm{d} t} \bigg] \\
&= E[Xe^{tX}] \\
\therefore \phi'(0) &= E[Xe^{0 \cdot X}] = E[X]
\end{align}
\tag{4.58}\]
\[
\begin{align}
\phi''(t) &= \frac{\mathrm{d} {\phi'(t)}}{\mathrm{d} t} \\
&= \frac{\mathrm{d} {E[Xe^{tX}]}}{\mathrm{d} t} \\
&= E\bigg[ \frac{\mathrm{d} {(Xe^{tX})}}{\mathrm{d} t} \bigg] \\
&= E[X^2e^{tX}] \\
\therefore \phi''(0) &= E[X^2]
\end{align}
\tag{4.59}\]
更一般的,在 \(t=0\) 处的 \(\phi(t)\) 的 \(n\) 阶导数等于 \(E[X^n]\) ,即:
\[
\phi^{n}(0) = E[X^n], \quad n \ge 1
\tag{4.60}\]
矩生成函数的一个重要特性是:独立 随机变量 之和的矩生成函数是每个 随机变量 的矩生成函数的乘积。假设 \(X\) 和 \(Y\) 是独立 随机变量 ,其矩生成函数分别为 \(\phi_X(t)\) 、\(\phi_Y(t)\) ,则 \(X+Y\) 的矩生成函数为:
\(\begin{align} \phi_{X+Y}(t) &= E[e^{t(X+Y)}] \\ &= E[e^{tX}e^{tY}] \\ &= E[e^{tX}]E[e^{tY}] \\ &= \phi_X(t)\phi_Y(t) \end{align}\)
如果 \(X\) 和 \(Y\) 是相互独立的,则 \(e^{tX}\) 和 \(e^{tY}\) 也是独立的,所以根据 定理 4.1 有 \(E[e^{tX}e^{tY}] = E[e^{tX}]E[e^{tY}]\) ,所以上式得证。
矩生成函数的另一个重要的特性是:矩生成函数唯一地确定了 随机变量 的概率分布。也就是说,矩生成函数和 随机变量 的分布函数之间存在一一对应的关系。
切比雪夫不等式和弱大数定律
我们从证明马尔可夫不等式(Markov’s inequality )开始本节的内容。
命题 4.3 马尔可夫不等式 :如果 \(X\) 是一个取值为非负数的 随机变量 ,则对于任意的 \(a \gt 0\) 有:
\(P\{X \ge a\} \le \frac{E[X]}{a}\)
证 . \(f\) 的连续 随机变量 \(X\) 的证明。
\[
\begin{align}
E[X] &= \int_{0}^{\infty}{xf(x) \mathrm{d} x} \\
&= \int_{0}^{a}{xf(x) \mathrm{d} x} + \int_{a}^{\infty}{xf(x) \mathrm{d} x} \\
& \ge \int_{a}^{\infty}{xf(x) \mathrm{d} x} \\
& \ge \int_{a}^{\infty}{af(x) \mathrm{d} x} \\
&= a\int_{a}^{\infty}{f(x) \mathrm{d} x} \\
&= aP\{X \ge a\} \quad \blacksquare
\end{align}
\]
作为推论,我们得到 命题 4.4 。
命题 4.4 契比雪夫不等式 :如果\(X\) 是一个均值为 \(\mu\) 方差为 \(\sigma^2\) 的随机变量,则对于任意的 \(k \gt 0\) 有:
\(P\{|X - \mu| \ge k\} \le \frac{\sigma^2}{k^2}\)
证 . \((X-\mu)^2\) 是一个非负的随机变量,因此,令 \(a=k^2\) ,然后根据 命题 4.3 所示的马尔科夫不等式有:
\[
P\{(X-\mu)^2 \ge k^2\} \le \frac{E[(X-\mu)^2]}{k^2}
\tag{4.61}\]
\((X-\mu)^2 \ge k^2\) 当且仅当 \(|X-\mu| \ge k\) ,所以 式 4.61 等价于:
\[
P\{|X-\mu| \ge k\} \le \frac{E[(X-\mu)^2]}{k^2} = \frac{\sigma^2}{k^2}
\tag{4.62}\]
证毕。\(\blacksquare\)
马尔可夫不等式和切比雪夫不等式的重要性在于:在只知道概率分布的均值或均值和方差的情况下,我们可以利用马尔可夫不等式和切比雪夫不等式推导出概率的界限。当然,如果实际的概率分布是已知的,那么就可以精确的计算出待计算的概率,我们也就不需要计算概率的界限。
习题 4.18 随机变量 ,其平均值为 50。
本周的产量超过 75 的概率可以说是多少?
如果已知一周的产量的方差等于 25,那么本周产量在 40 和 60 之间的概率是多少?
解 4.18 . \(X\) 为工厂一周的产量。
利用马尔科夫不等式可知:
\(P\{X \gt 75\} \le \frac{E[X]}{75} = \frac{50}{75} = \frac{2}{3}\)
利用切比雪夫不等式可知:
\(P\{|X-50| \ge 10\} \le \frac{\sigma^2}{10^2} = \frac{1}{4}\) ,所以:
$\(P\{|X-50| \lt 10\} \ge 1 - \frac{1}{4} = \frac{3}{4}\) 。
因此,本周产量在 40 和 60 之间的概率最小是 0.75。\(\blacksquare\)
在 式 4.62 中,令 \(k = k\sigma\) ,我们可以将切比雪夫不等式改写为:
\[
P\{|X - \mu| \ge k\sigma\} \le \frac{1}{k^2}
\tag{4.63}\]
因此,随机变量 与其 均值 相差超过 \(k\) 个 标准差 的概率最大为 \(\frac{1}{k^2}\) 。
在本节的最后,我们将用切比雪夫不等式来证明弱大数定律(weak law of large numbers )。弱大数定律指出:在一个独立同分布的 随机变量 序列中,当 \(n\) 趋向于无穷大时,前 \(n\) 个 随机变量 的平均数(average )和该随机变量的均值(mean )的差值超过 \(\varepsilon\) 的概率为 0。
定理 4.2 弱大数定律 :令 \(X_1, X_2,...\) 是一个独立同分布的 随机变量 序列,每个 随机变量 的均值都为 \(\mu\) (\(E[X_i] = \mu\) )。则,对于任意的 \(\varepsilon \gt 0\) ,有:
\(P\bigg\{ \big| \frac{X_1 + X_2 + ... + X_n}{n} - \mu \big| \gt \varepsilon \bigg\} \rightarrow 0, \quad n \rightarrow \infty\)
证 . 随机变量 的方差 \(\sigma^2\) 为有限数的附加假设下证明 定理 4.2 。因为:
\(E\bigg[\frac{X_1 + X_2 + ... + X_n}{n}\bigg] = \mu\) ,\(\textup{Var}\bigg(\frac{X_1 + X_2 + ... + X_n}{n}\bigg) = \frac{\sigma^2}{n}\)
所以,根据 命题 4.4 的切比雪夫不等式有:
\(P\bigg\{ \big| \frac{X_1 + X_2 + ... + X_n}{n} - \mu \big| \gt \varepsilon \bigg\} \le \frac{\sigma^2}{n \varepsilon^2}\)
证毕。\(\blacksquare\)
假设我们独立执行某个试验多次,令 \(E\) 为某个固定 事件 ,用 \(P(E)\) 表示 \(E\) 在给定试验中发生的概率。令
\(X_i = \begin{cases} 1, \quad & 第 i 次试验中 E 发生\\ 0, \quad & 第 i 次试验中 E 不发生 \end{cases}\)
则 \(X_1+X_2+...+X_n\) 表示在 \(n\) 次试验中,\(E\) 发生的次数。因为 \(E[X_i]=P(E)\) ,所以根据弱大数定律,对于任意的 \(\varepsilon \gt 0\) ,无论 \(\varepsilon\) 有多小,随着 \(n\) 的增加,前 \(n\) 次试验中 \(E\) 发生的比例与 \(P(E)\) 的差值超过 \(\varepsilon\) 的概率会变为 0。
习题
根据考试成绩对 5 名男性和 5 名女性进行排名。假设所有人的分数都不相同,并且所有的 \(10!\) 种可能的排名的可能性都相等。令 \(X\) 表示女性获得的最高名次(例如,如果排名第 1 的是男性,而排名第 2 的是女性,则 \(X=2\) )。找出 \(P\{X=i\}, i=1,2,3,...,8,9,10\) 。
设 \(X\) 表示抛 \(n\) 次硬币得到的正面向上的次数和反面向上的次数之差,则 \(X\) 的可能值是多少?
在习题 2 中,如果假设硬币是公平的,对于 \(n=3\) ,则 \(X\) 可能取值的对应的概率是多少?
随机变量 \(X\) 的分布函数为: \[
F(x) = \begin{cases}
0, \quad & x \lt 0 \\
\frac{x}{2}, \quad & 0 \le x \lt 1 \\
\frac{2}{3}, \quad & 1 \le x \lt 2 \\
\frac{11}{12}, \quad & 2 \le x \lt 3 \\
1, \quad & 3 \le x \\
\end{cases}
\]
画出分布函数的图
计算 \(P\{X \gt \frac{1}{2}\}\) ?
计算 \(P\{2 \lt X \le 4\}\) ?
计算 \(P\{X \le 3\}\) ?
计算 \(P\{X = 1\}\) ?
假设随机变量 \(X\) 的概率密度函数为: \[
f(x) = \begin{cases}
cx^3, \quad & 0 \le x \le 1 \\
0, \quad & 其他
\end{cases}
\]
计算 \(c\) 的值?
计算 \(P\{0.4 \lt X \lt 0.8\}\) ?
计算机在故障前运行的小时数是一个连续随机变量,其概率密度函数为:
\[
f(x) = \begin{cases}
\lambda e^{-\frac{x}{100}}, \quad & x \ge 0 \\
0, \quad & x \lt 0
\end{cases}
\]
一台计算机在故障前工作了 50 到 150 小时的概率是多少?
工作不到 100 小时的概率是多少?
收音机中某种电子管的寿命(以小时为单位)是一个随机变量,其概率密度函数为:
\[
f(x) = \begin{cases}
0, \quad & x \le 100 \\
\frac{100}{x^2}, \quad & x \gt 100
\end{cases}
\]
一台收音机中的 5 个这样的电子管中恰有 2 个必须在 150 小时内更换的概率是多少?假设在这段时间内,必须更换第 \(i\) 个电子管的 事件 \(E_i, i=1,2,3,4,5\) 是独立的。
如果 \(X\) 的概率密度函数为:
\[
f(x) = \begin{cases}
ce^{-2x}, \quad & 0 \lt x \lt \infty \\
0, \quad & x \lt 0
\end{cases}
\]
计算 \(c\) ?
计算 \(P\{X \gt 2\}\) ?
我们要检测 5 个晶体管,我们以随机的顺序每次检测 1 个晶体管,并检查哪一个晶体管有缺陷。假设 5 个晶体管中有 3 个有缺陷,令 \(N_1\) 表示发现第 1 个缺陷晶体管时我们检测的次数,让 \(N_2\) 表示发现第 2 个缺陷晶体管时额外增加的检测次数。计算 \(N_1\) 和 \(N_2\) 的联合概率质量函数。
\(X\) 和 \(Y\) 的联合概率密度函数为:
\(f(x,y)=\frac{6}{7}\big(x^2 + \frac{xy}{2}\big), \ 0 \lt x \lt 1, \ 0 \lt y \lt 2\)
验证这确实是一个联合密度函数?
计算 \(X\) 的边缘密度函数?
计算 \(P\{X \gt Y\}\) ?
令 \(X_1, X_2, ..., X_n\) 是符合 \(U(0,1)\) 的均匀分布的独立随机变量。令 \(M = max(X_1, X_2, ...,X_n)\) ,则 \(M\) 的分布函数为:
\(F_M(x) = x^n, \ 0 \le x \le 1\)
计算 \(M\) 的概率密度函数?
\(X\) 、\(Y\) 的联合密度函数为:
\(f(x,y)=\begin{cases} xe^{-(x+y)}, \quad & x \gt 0, y \gt 0 \\ 0, \quad & 其它 \end{cases}\)
计算 \(X\) 的边缘密度函数?
计算 \(Y\) 的边缘密度函数?
\(X\) 和 \(Y\) 是独立的吗? \(X\) 、\(Y\) 的联合概率密度函数为:
\(f(x,y)=\begin{cases} 2, \quad & 0 \lt x \lt y, 0 \lt y \lt 1 \\ 0, \quad & 其它 \end{cases}\)
计算 \(X\) 的边缘密度函数?
计算 \(Y\) 的边缘密度函数?
\(X\) 和 \(Y\) 是独立的吗? 如果 \(X\) 和 \(Y\) 的联合密度函数可以分解为仅依赖于 \(x\) 的部分和仅依赖于 \(y\) 的部分,则 \(X\) 和 \(Y\) 是独立的。如果:
\(f(x,y)=k(x)h(y), \ -\infty \lt x \lt \infty, \ -\infty \lt x \lt \infty\)
证明,\(X\) 、\(Y\) 是相互独立的。
习题 14 与习题 12 和习题 13 的结果一致吗?
假设 \(X\) 、\(Y\) 是独立的连续随机变量,证明:
\(P\{X + Y \le a\} = \int_{-\infty}^{\infty}{F_X(a-y)f_Y(y)\mathrm{d} y}\) \(P\{X \le Y\} = \int_{-\infty}^{\infty}{F_X(y)f_Y(y)\mathrm{d} y}\)
其中,\(f_Y\) 是 \(Y\) 的边缘概率密度函数,\(F_X\) 是 \(X\) 的边缘分布函数。
当电流 \(I\) (单位为安培)流过电阻 \(R\) 时(单位为欧姆),产生的功率(单位为瓦特)为 \(W=I^2R\) 。 假设 \(I\) 和 \(R\) 是独立随机变量且其概率密度函数为:
\(f_I(x) = 6x(1-x), \quad 0 \le x \le 1\)
\(f_R(x) = 2x, \quad 0 \le x \le 1\)
计算 \(W\) 的概率密度函数?
在 例 4.5 中,计算所选择的家庭有 2 个女孩的条件概率质量函数?
计算 \(X\) 在 \(Y=y\) 时的条件概率密度函数:
\(X\) 、\(Y\) 的联合概率密度函数如习题 10\(X\) 、\(Y\) 的联合概率密度函数如习题 13 证明 \(X\) 、\(Y\) 是独立随机变量当且仅当:
\(X\) 、\(Y\) 是离散随机变量且 \(P_{X|Y}(x|y)=p_X(x)\) \(X\) 、\(Y\) 是连续随机变量且 \(f_{X|Y}(x|y)=f_X(x)\) 计算习题 1 中随机变量的期望?
计算习题 3 中随机变量的期望?
每天晚上,不同的气象学家会预测第二天下雨的“概率”。为了判断这些人的预测水平,我们将按如下的规则给他们打分:如果气象学家预测明天下雨的概率为 \(p\) ,那么他们的得分为:
如果明天确实下雨了,得分为:\(1 - (1 - p)^2\)
如果明天没有下雨,得分为:\(1 - p^2\)
对于这些打分,我们将跟踪一定的时间,并得出结论:平均打分最高的气象学家就是最佳天气预测者。现在,假设某个气象学家已经了解到了打分的规则,并希望最大化自己的打分。如果该气象学家真的相信明天下雨的概率为 \(p^*\) ,那么为了最大化自己的打分,他预测明天下雨的概率 \(p\) 应该是多少?
一家保险公司有一种保单,大意是:如果某个事件 \(E\) 在一年内发生,则他们必须支付一笔钱 \(A\) 。如果保险公司估计 \(E\) 在一年内发生的概率为 \(p\) ,保险公司应该向客户收取多少费用,以使得他们的预期利润将是 \(A\) 的 10%?
4 辆载有来自同一所学校的 148 名学生的公共汽车来到一个足球场。公共汽车的载客量分别为:40名、33名、25名和50名。随机选择一名学生,令 \(X\) 表示随机选择的这个学生所在的公共汽车上的学生数量。对于 4 辆车的 4 名司机,随机选择 1 名司机,令 \(Y\) 表示该司机驾驶的公共汽车上的学生数量。
你认为 \(E[X]\) 和 \(E[Y]\) 哪一个更大?为什么?
计算 \(E[X]\) 和 \(E[Y]\) 。
在一场多局游戏比赛中,两个参赛队伍中,如果有一个首先赢得 \(i\) 局游戏,则游戏结束。假设每一局比赛都是独立的,且 \(A\) 队获胜概率是 \(p\) 。当 \(i=2\) 时:
计算游戏局数的期望?
证明当 \(p=\frac{1}{2}\) 时,该期望值最大?
\(X\) 的概率密度函数为:
\(f(x)=\begin{cases} a + bx^2, \quad & 0 \le x \le 1\\ 0, \quad & 其它 \end{cases}\)
如果 \(E[X] = \frac{3}{5}\) ,计算 \(a\) 和 \(b\) 。
某电子管的寿命(单位为小时)是一个随机变量,其概率密度函数为:
\(f(x) = a^2xe^{-ax}, \quad x \ge 0\)
计算该电子管的寿命的期望?
令 \(X_1, X_2,...,X_n\) 是独立同分布的随机变量,其概率密度函数为:
\(f(x) = \begin{cases} 1, \quad & 0 \lt x \lt 1\\ 0, \quad & 其它 \end{cases}\)
计算:
\(E[Max(X_1, X_2, ..., X_n)]\) \(E[Min(X_1, X_2, ..., X_n)]\) 假设 \(X\) 的概率密度函数为:
\(f(x)=\begin{cases} 1, \quad & 0 \lt x \lt 1\\ 0, \quad & 其它 \end{cases}\)
根据如下的要求计算 \(E[X^n]\) :
先计算 \(X^n\) 的概率密度,然后根据期望的定义计算 \(E[X^n]\)
利用 命题 4.1 计算 \(E[X^n]\)
修理个人电脑所需的时间(以小时为单位)是一个随机变量,其密度函数为:
\(f(x)=\begin{cases} \frac{1}{2}, \quad & 0 \lt x \lt 2\\ 0, \quad & 其它 \end{cases}\)
修理的费用取决于修理所需的时间,当修理所需时间为 \(x\) 时,费用为 \(40 + 30 \sqrt{x}\) 。计算修理个人电脑的费用的期望。
如果 \(E[X] = 2\) ,\(E[X^2] = 8\) ,计算:
\(E[(2 + 4X)^2]\) ?\(E[X^2 + (X+1)^2]\) ? 从包含 17 个白球和 23 个黑球的盒子中随机选择 10 个球。令 \(X\) 表示所选白球的数量。利用如下的方式计算 \(E[X]\) :
定义适当的指示随机变量 \(X_i, i=1,...,10\) ,以满足 \(X = \sum_{i=1}^{10}{X_i}\) 。
定义适当的指示随机变量 \(Y_i, i=1,...,17\) ,以满足 \(X = \sum_{i=1}^{17}{Y_i}\) 。
如果 \(X\) 是具有分布函数 \(F\) 的连续随机变量,则其中位数(median )的定义为令 \(F(m)=\frac{1}{2}\) 的 \(m\) 的值。如果随机变量的概率密度函数如下所示,计算其中位数:
\(f(x) = e^{-x}, \quad x \ge 0\) 。\(f(x) = 1, 0 \le x \le 1\) 。 在预测随机变量的值方面,中位数和均值一样都是很重要的概念。如前所述(式 4.46 ),随机变量的均值是从最小化误差平方的期望的角度所得到的最佳预测器。而中位数则是通过最小化绝对误差的期望所得到的最佳预测器。也就是说,当 \(c\) 是 \(X\) 的分布函数的中位数时,\(E[|X − c|]\) 的值最小。当 \(X\) 是连续随机变量,且其分布函数和密度函数分别为 \(F\) 和 \(f\) 时,请证明如上的关于中位数的结论。提示:
\[
\begin{align}
E[|X-c|] &= \int_{-\infty}^{\infty}{|x-c|f(x)\mathrm{d} x} \\
&= \int_{-\infty}^{c}{|x-c|f(x)\mathrm{d} x} + \int_{c}^{\infty}{|x-c|f(x)\mathrm{d} x} \\
&= \int_{-\infty}^{c}{(c-x)f(x)\mathrm{d} x} + \int_{c}^{\infty}{(x-c)f(x)\mathrm{d} x} \\
&= cF(c) - \int_{-\infty}^{c}{xf(x)\mathrm{d} x} + \int_{c}^{\infty}{xf(x)\mathrm{d} x} - c[1 - F(c)]
\end{align}
\]
然后利用微积分求 \(c\) 的最小值。
对于随机变量的分布函数 \(F\) ,如果有 \(F(m_p)=p\) ,则我们称 \(m_p\) 为 \(100p\) -百分位数。如果一个随机变量的概率密度函数为:
\(f(x)=2e^{-2x}, \quad x \ge 0\)
求 \(m_p\) 。
一个社区由 100 对已婚夫妇组成。如果这个社区有 50 人去世了,那么剩下的 50 人中包含的夫妻数量的期望是多少?假设去世的人群随机来 \(\left(\begin{array}{cc} 200 \\ 50 \end{array}\right)\) 中的任何一组。提示:对于 \(i=1,...,100\) ,令
\(X_i = \begin{cases}1, \quad & 夫妻中没有人去世\\0, \quad & 其它\end{cases}\)
某个试验的成功概率为 \(p\) ,如果独立执行 \(n\) 次试验,计算其成功次数的期望和方差?计算中,试验之间的独立性是有必要的吗?
假设 \(X\) 取值 1、2、3、4 中的任何一个数的概率都是一致的,计算:
令 \(p_i=P\{X=i\}\) ,假设 \(p_1+p_2+p_3=1\) 。如果 \(E[X]=2\) ,求:
\(p_1\) 、\(p_2\) 、\(p_3\) 的最大值?\(Var(X)\) 的最小值? 抛 3 次硬币,计算其正面向上的次数的期望和方差?
该题涉及到 例 4.13 所示的友谊悖论。我们随机选择一个人 \(X\) ,并从 \(X\) 的好友中随机选择一个人 \(W\) 。也就是说,在 \(X\) 的 \(n\) 位好友中,\(W\) 是 \(X\) 的好友的概率是 \(\frac{1}{n}\) 。在 例 4.13 中,已经证明了 \(E[f(W)] \ge E[f(X)]\) ,即随机选择的某个人的平均朋友数不大于其随机选择的朋友的平均朋友数。使用 图 4.5 给出的朋友圈证明该结论是正确的。
某种零件的重量是一个随机变量 \(X\) ,其概率密度函数为:
\(f(z)=\begin{cases} z-8, \quad & 8 \le z \le 9 \\ 10-z, \quad & 9 \lt z \le 10 \\ 0, \quad & 其它 \end{cases}\)
计算随机变量 \(X\) 的期望和方差?
工厂以 2 元的固定价格出售该零件,并且工厂保证:任何购买该零件的客户,如果发现该零件的重量低于 8.25,他们将退还货款。工厂生产该零件的成本与零件的重量关系为 \(\frac{x}{15} + 0.35\) 。计算每个零件的预期利润?
在某次给定的选举中,令随机变量 \(X_i\) 表是对候选人 \(i\) 的投票支持率,假设 \(X_1\) 和 \(X_2\) 的概率密度函数为:
\(f_{X_1, X_2}(x,y)=\begin{cases} 3(x+y), \quad & x \ge 0, y \ge 0, 0 \le x +y \le 1\\ 0, \quad & 其它 \end{cases}\)
计算 \(X_1\) 和 \(X_2\) 的边缘密度函数?
对于 \(i=1,2\) ,计算 \(E[X_i]\) 和 \(\textup{Var}(X_i)\) ?
我们会根据产品的缺陷数量和生产厂家对产品进行分类。设随机变量 \(X_1\) 表示单位产品的缺陷量(取值为 0,1,2,3),随机变量 \(X_2\) 表示工厂编号(取值为 1,2)。随机选择一个产品,其联合概率质量函数如下表所示:
\(X_1\) = 0\(\frac{1}{8}\) \(\frac{1}{16}\)
\(X_1\) = 1\(\frac{1}{16}\) \(\frac{1}{16}\)
\(X_1\) = 2\(\frac{3}{16}\) \(\frac{1}{8}\)
\(X_1\) = 3\(\frac{1}{8}\) \(\frac{1}{4}\)
计算 \(X_1\) 、\(X_2\) 的边缘概率分布?
计算 \(E[X_1]\) ,\(E[X_2]\) ,\(\textup{Var}(X_1)\) ,\(\textup{Var}(X_2)\) ,\(\textup{Cov}(X_1, X_2)\) ?
计算 习题 44 中的随机变量的相关性 \(\textup{Corr}(X_1, X_2)\) ?
验证 式 4.53 ?
用数学归纳法证明 式 4.54 ?
令 \(X\) 的方差为 \(\sigma_x^2\) ,\(Y\) 的方差为 \(\sigma_y^2\) 。
当 \(0 \le \textup{Var}(\frac{X}{\sigma_x} + \frac{Y}{\sigma_y})\) 时,有 \(-1 \le \textup{Corr}(X,Y)\) 。
当 \(0 \le \textup{Var}(\frac{X}{\sigma_x} - \frac{Y}{\sigma_y})\) 时,有 \(-1 \le \textup{Corr}(X,Y) \le 1\) 。
当 \(\textup{Var}(Z) = 0\) 时意味着 \(Z\) 是一个常数。
证明:
当 \(Y=ax +b\) 时,\(\textup{Corr}(X,Y)\) 等于 1 或者 -1?
当 \(a > 0\) 时,\(\textup{Corr}(X,Y) = 1\) ,当 \(a < 0\) 时,\(\textup{Corr}(X,Y) = -1\) ?
一个试验的结果取值为 1、2、3,并且各自的概率为 \(p_1,p_2,p_3\) ,并且 \(sum_{i=1}^{3} = 1\) 。对于 \(n\) 次这样的相互独立的试验,令 \(N_i\) 表示实验结果为 \(i\) 的次数,证明:
\(\textup{Cov}(N_1, N_2) = -np_1p_2\) ?请解释为什么如上的协方差是负数?
提示:对于 \(i=1,...,n\) ,
令 \(X_i=\begin{cases} 1, \quad & 第 i 次试验的结果为 1\\ 0, \quad & 第 i 次试验的结果不为 1 \end{cases}\) 。
同理,令 \(Y_j=\begin{cases} 1, \quad & 第 j 次试验的结果为 2\\ 0, \quad & 第 j 次试验的结果不为 2 \end{cases}\) 。
然后证明 \(N_1 = \sum_{i=1}^{n}X_i\) ,\(N_2 = \sum_{j=1}^{n}Y_i\) ,然后利用 命题 4.2 和 定理 4.1 来证明 \(\textup{Cov}(N_1, N_2)\) 。
对于 习题 4.12 ,计算 \(\textup{Cov}(X_i,X_j)\) ,并用该结果证明 \(\textup{Var}(X) = 1\) 。
如果 \(X_1\) 和 \(X_2\) 的概率分布函数相同,证明:\(\textup{Cov}(X_1 - X_2, X_1 + X_2) = 0\) (注意,此处没有假定 \(X_1\) 和 \(X_2\) 相互独立)。
假设 \(X\) 的概率密度函数为:\(f(x)=e^{-x}, \ x \gt 0\) 。
计算 \(X\) 的矩生成函数,并用结果来确定 \(X\) 的均值和方差。
直接根据概率密度函数计算 \(X\) 的均值并用来该值来校验上一步中得出的结果。
如果 \(X\) 的概率密度函数为:\(f(x) = 1, \ 0 \lt x \lt 1\) 。
计算 \(E[e^{tX}]\) 。
对 \(E[e^{tX}]\) 求 \(n\) 阶导数以得到 \(E[X^n]\) ,并校验结果。
假设随机变量 \(X\) 的均值和方差都是 20,计算 \(P\{0 \le X \le 40\}\) ?
根据过去的经验,教授知道学生期末考试的成绩是一个随机变量,并且其平均值为 75。
学生考试成绩超过 85 的最大概率是多少?
假设教授知道学生考试成绩的方差为 25,那么学生成绩在 65 到 85 之间的概率如何?
最少有多少学生参加考试,才能确保该班级的平均水平在 70 到 80 之间的概率至少为 0.9?
令 \(X\) 的分布函数为 \(F_X\) ,\(Y\) 的分布函数为 \(F_Y\) ,假设对于常数 \(a > 0\) ,\(b > 0\) ,有
\(F_X(x) = F_Y\bigg(\frac{x-a}{b}\bigg)\)
用 \(E[Y]\) 来确定 \(E[X]\) ?
用 \(\textup{Var}(Y)\) 来确定 \(\textup{Var}(X)\) ?
提示:\(X\) 与哪个随机变量的分布相同?