代码
dbinom(70, 100, 0.75)[1] 0.045753815 特殊的随机变量
在实际应用中，某些类型的 随机变量 会反复出现。在本章中，我们将研究经常应用到的几种 随机变量。
5.1 伯努利分布和二项分布
假设一项试验的结果只有两种：“成功”或“失败”。当实验结果是“成功”时，令 \(X=1\)；当结果是“失败”时，令 \(X=0\)。令 \(p\) 为“成功”的概率（\(0 \le p \le 1\)），那么 \(X\) 的概率质量函数为：
\[ \begin{align} & P\{X = 0\} = 1 - p \\ & P\{X = 1\} = p \end{align} \tag{5.1}\]
一个 随机变量 \(X\) 的概率质量函数如果满足 式 5.1 （其中 \(p \in (0,1)\)），我们称 \(X\) 是 伯努利随机变量（Bernoulli random variable，以瑞士数学家 James Bernoulli 的名字命名）。伯努利随机变量的期望为：
\(E[X] = 1 \cdot P\{X = 1\} + 0 \cdot P\{X = 0\} = p\)
也就是说，伯努利随机变量的期望就是该随机变量取值为 1 时的概率。
假设现在要执行 \(n\) 个独立的试验，其中每个试验“成功”的概率为 \(p\) 并且“失败”的概率为 \(1-p\)。如果 \(X\) 表示 \(n\) 个试验中的成功次数，那么我们称 \(X\) 是参数为 \((n, p)\) 的二项随机变量（binomial random variable）。
参数为 \((n, p)\) 的二项随机变量的概率质量函数为：
\[ P\{X=i\} = \left(\begin{array}{cc} n \\ i \end{array}\right)p^i(1-p)^{n-i}, \qquad i = 0,1,...,n \tag{5.2}\]
其中，\(\left(\begin{array}{cc} n \\ i \end{array}\right) = \frac{n!}{i!(n-i)!}\) 是从 \(n\) 个物体中抽取 \(i\) 个物体的不同的抽取方式数量。我们可以按照如下的步骤来校验 式 5.2 的正确性：
- 首先，假设这 \(n\) 次试验是相互独立的，则在任何一个特定的试验序列中出现 \(i\) 次“成功” \(n-i\) 次失败的概率为 \(p^i(1-p)^{n-i}\)。
- 其次，因为在 \(n\) 次试验中，出现 \(i\) 次“成功” \(n-i\) 次失败的不同的试验数量为 \(\left(\begin{array}{cc} n \\ i \end{array}\right)\)，因此 \(p^i(1-p)^{n-i}\) 需要再乘以 \(\left(\begin{array}{cc} n \\ i \end{array}\right)\)。
例如，如果 \(n = 5\)，\(i = 2\)，则成功 2 次的总的试验数量为 \(\left(\begin{array}{cc} 5 \\ 2 \end{array}\right)\)，也就是：
\((s,s,f,f,f) \quad (f,s,s,f,f) \quad (f,f,s,f,s)\)
\((s,f,s,f,f) \quad (f,s,f,s,f) \quad (s,f,f,s,f)\)
\((f,s,f,f,s) \quad (f,f,f,s,s) \quad (s,f,f,f,s) \quad (f,f,s,s,f)\)
其中，\((f,s,f,s,f)\) 意味着：第 2 次和第 4 次试验的结果是“成功”的。由于 \(\left(\begin{array}{cc} 5 \\ 2 \end{array}\right)\) 种实验结果种，每一种的概率都为 \(p^2(1−p)^3\)，因此在 5 次实验中出现 2 次成功的概率为 \(\left(\begin{array}{cc} 5 \\ 2 \end{array}\right)p^2(1-p)^3\)。 我们可以发现 \(p(i)\) 的和为 1，也就是说：
\(\sum_{i=0}^{\infty}{p(i)} = \sum_{i=0}^{n} \left(\begin{array}{cc} n \\ i \end{array}\right) p^i (1-p)^{n-i} = \big( p + (1-p)\big)^n = 1\)
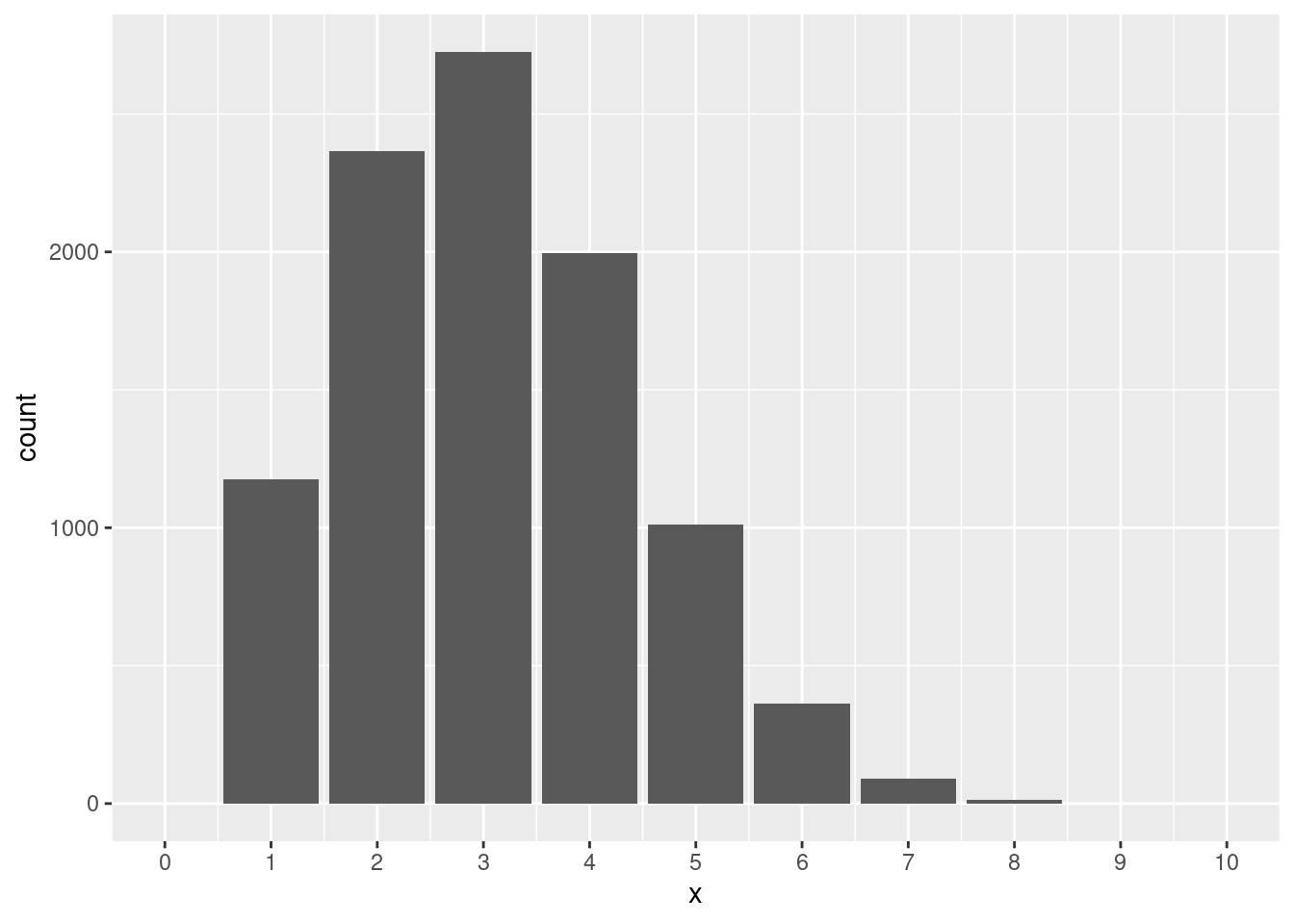
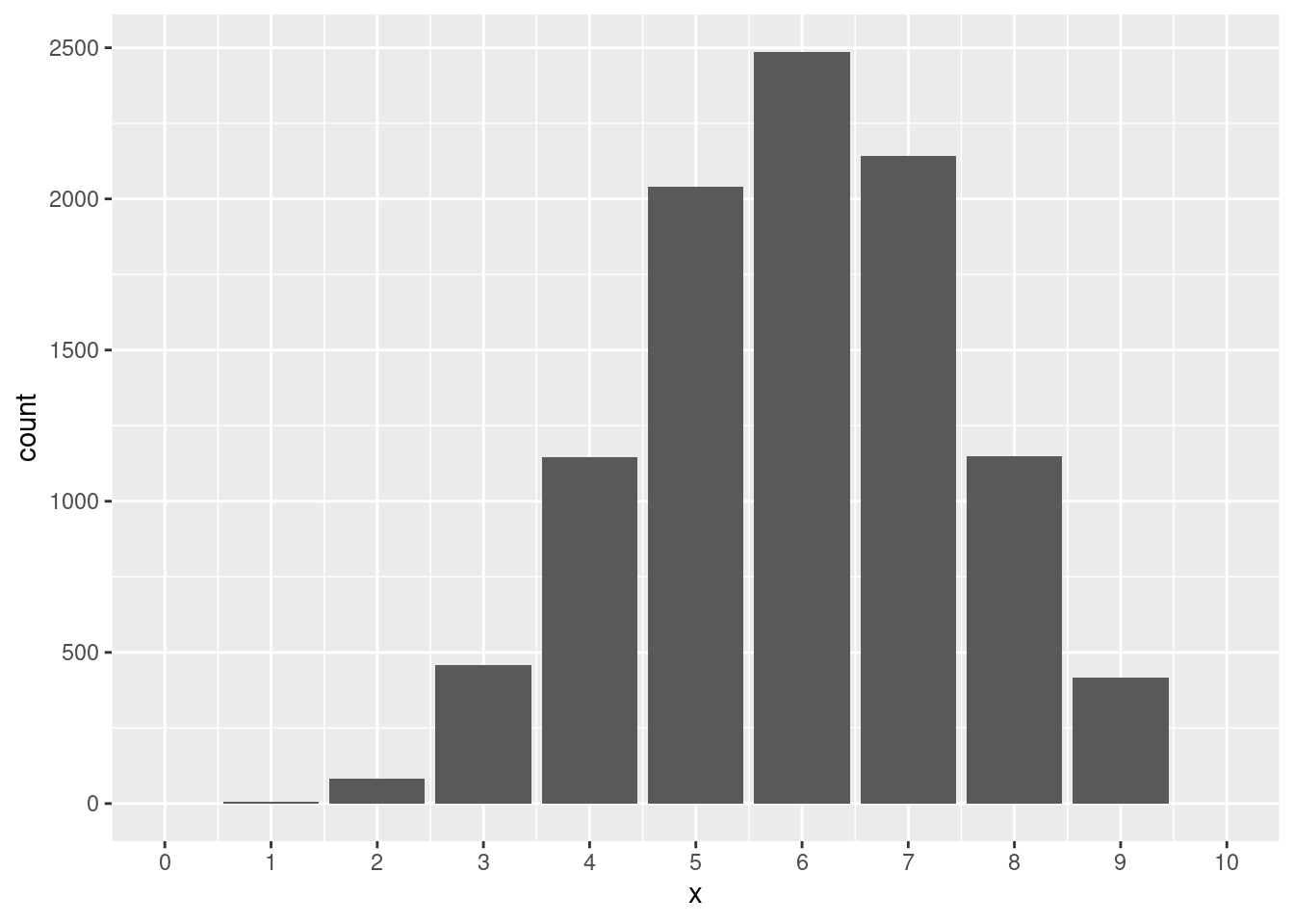
图 5.1 给出了三个参数分别为 \((10, 0.5)\)，\((10, 0.3)\)，\((10, 0.6)\) 的二项随机变量的概率质量函数。其中，当 \(p=0.5\) 时，图形是对称的；当 \(p=0.3\) 时，图形是右偏的；当 \(p=0.6\) 时，图形是左偏的（如 小节 2.5 所示）。
代码
library(ggplot2)
n <- 10
p <- 0.5
random_numbers <- rbinom(n = 10000, size = n, prob = p)
df <- data.frame(x = random_numbers)
ggplot(df, aes(x = x)) +
geom_bar() +
scale_x_continuous(breaks = seq(0,10,1), limits = c(0, 10))
p <- 0.3
random_numbers <- rbinom(n = 10000, size = n, prob = p)
df <- data.frame(x = random_numbers)
ggplot(df, aes(x = x)) +
geom_bar() +
scale_x_continuous(breaks = seq(0,10,1), limits = c(0, 10))
p <- 0.6
random_numbers <- rbinom(n = 10000, size = n, prob = p)
df <- data.frame(x = random_numbers)
ggplot(df, aes(x = x)) +
geom_bar() +
scale_x_continuous(breaks = seq(0,10,1), limits = c(0, 10))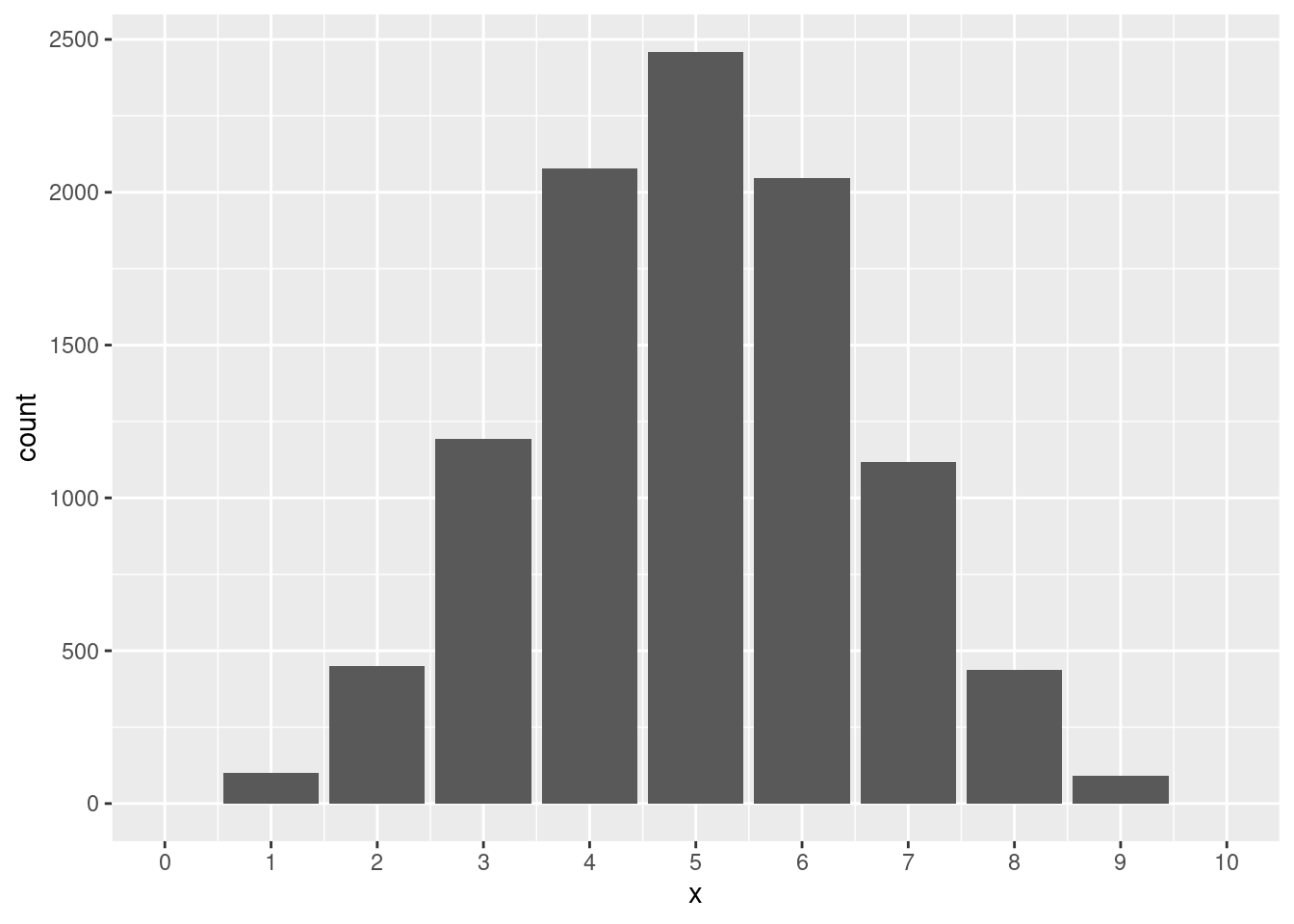
习题 5.1 某家公司生产的磁盘的次品率为 0.01，该公司按 10 个磁盘为一包的方式打包出售磁盘，并保证每包的 10 个磁盘中只要有超过 1 个次品就可以退货。那么，该公司的退货比例是多少？如果有人买了三包磁盘，其中退一包的概率是多少？
解 5.1. 若果 \(X\) 是每包磁盘中的次品数量，则 \(X\) 是一个参数为 \((10, 0.01)\) 的二项随机变量。因此，对于 1 包磁盘而言，退货的概率为：
\(P\{X \gt 1\} = 1 - P\{X = 0\} - P\{X = 1\} \approx 0.05\)
因为每包磁盘的退货率都是 0.005 并且都是相互独立的，根据大数定律，从长远来看，该公司的退货比例为 0.5%。
根据上述情况，顾客购买的三包磁盘中可以退货的包数是一个参数为 \((3, 0.005)\) 的二项随机变量。因此，三包磁盘中，恰好有一包退货的概率为 \(\left(\begin{array}{cc} 3 \\ 1 \end{array}\right) \cdot 0.005 \cdot 0.995^2 = 0.015\)。\(\blacksquare\)
习题 5.2 一个人的眼睛的颜色由单独的一对基因决定，其中棕色基因是显性基因，蓝色基因是隐形基因。这意味着：如果一个人的基因对中的两个基因都是蓝色基因，则他的眼睛是蓝色的；而如果他的基因对中的两个基因都是棕色的或者有一个棕色基因和一个蓝色基因，则他的眼睛是棕色的。每个人的基因对都是随机从父母的基因对中选择一个基因而构成的。如果一对夫妇的眼睛都是棕色的，并且他们的第一个孩子的眼睛是蓝色的，那么他们的另外四个孩子中的两个（另外的 4 个孩子都不是双胞胎）也有蓝色眼睛的概率是多少？
解 5.2. 首先，因为他们最大的孩子的眼睛是蓝色的，因此这对夫妇的基因对均为一个棕色基因和一个蓝色基因（对于父母中有一个人有两个棕色基因，那么每个孩子都至少会得到一个棕色基因，因此所有孩子的眼睛都是棕色的）。这对夫妇的孩子的眼睛为蓝色的概率等于孩子的基因对中的基因都是蓝色基因的概率，即 \(\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}\)。又因为其他四个孩子中的每个孩子的眼睛是蓝色的概率均为 \(\frac{1}{4}\)，因此，他们中正好有两人的眼睛是蓝色的概率是：
\(\left(\begin{array}{cc} 4 \\ 2 \end{array}\right) \cdot (\frac{1}{4})^2 \cdot (\frac{3}{4})^2 = \frac{27}{128}\)。\(\blacksquare\)
习题 5.3 一个通信系统由 \(n\) 个组件组成，每个组件都是相互独立的，并且每个组件可以正常工作的概率都是 \(p\)。如果至少有一半的组件可以正常工作，整个系统就能够有效的运行。
- 当 \(p\) 为多少时，5-组件系统比3-组件系统的稳定性更高？
- 更一般的，当 \(p\) 为多少时，\(2k+1\)-组件系统比 \(2k-1\)-组件系统更稳定？
解 5.3.
因为可工作的组件数量是参数为 \((n,p)\) 的二项随机变量，因此5-组件系统可以正常工作的概率为：
\(\left(\begin{array}{cc} 5 \\ 3 \end{array}\right) p^3 (1-p)^2 + \left(\begin{array}{cc} 5 \\ 4 \end{array}\right) p^4 (1-p) + p^5\)
3-组件系统可以正常工作的概率为：
\(\left(\begin{array}{cc} 3 \\ 2 \end{array}\right) p^2 (1-p) + p^3\)
因此，当5-组件系统更稳定时，有：
\(10p^3(1−p)^2 +5p^4(1−p)+p^5 \ge 3p^2(1−p)+p^3\)
于是有：\(3(p−1)^2(2p−1) \ge 0\)，即 \(p \ge \frac{1}{2}\)。
一般来说，当且仅当 \(p \ge \frac{1}{2}\) 时，\(2k+1\)-组件系统比 \(2k-1\)-组件系统更稳定。为了证明这一点，考虑一个 \(2k+1\)-组件系统， 并令 \(X\) 表示前 \(2k-1\) 个组件构成的系统可以正常运行时其正常工作的组件数量。然后有：
\(P_{2k+1}=P\{X \ge k + 1\} + P\{X = k\}(1 − (1 − p)^2) + P\{X = k − 1\}p^2\)
因此，\(2k+1\)-组件系统可以正常运行时，需要满足如下条件：
- 或者 \(X \ge k+1\)
- 或者 \(X = k\) 并且剩余的 2 个组件中至少有 1 个可以正常工作
- 或者 \(X = k - 1\) 并且剩余的 2 个组件均可以正常工作
因为 \(P_{2k-1} = P\{X \ge k\} = P\{X=k\} + P\{X \ge k+1\}\)，故而：
\[ \begin{align} P_{2k + 1} - P_{2k - 1} &= P\{X = k−1\}p^2 − (1−p)^2P\{X = k\} \\ &= \left(\begin{array}{cc} 2k - 1 \\ k - 1 \end{array}\right) p^{k-1}(1-p)^kp^2 - (1-p)^2 \left(\begin{array}{cc} 2k - 1 \\ k \end{array}\right) p^k (1-p)^{k-1} \\ &= \left(\begin{array}{cc} 2k-1 \\ k \end{array}\right) p^k (1-p)^k (p - (1-p)) \\ \ge 0 \Leftrightarrow p \ge \frac{1}{2} \quad \blacksquare \end{align} \]
习题 5.4 假设一家计算机硬件制造商生产的芯片的次品率为 10%。如果我们订购 100 个这样的芯片，我们收到的芯片中的次品数量 \(X\) 会是二项随机变量吗？
解 5.4. 如果每个芯片可以工作的概率为 0.9 并且不同芯片之间可以工作的事件之间是相互独立的，则随机变量 \(X\) 将是一个参数为 \((100, 0.1)\) 的二项随机变量。当我们知道生产的芯片中有 10% 是次品时，\(X\) 是否是一个二项随机变量还取决于其他的因素。例如，假设在给定的一天中生产的所有芯片总是要么功能正常，要么是次品（其中 90% 的天数生产的芯片是功能正常的）。在这种情况下，如果我们知道我们的 100 个芯片都是在同一天生产的，此时芯片之间功能正常的事件并不是独立的，所以 \(X\) 将不是一个二项随机变量。事实上，在这种情况下，我们会得到：
\(P\{X = 100\} = 0.1\)
\(P\{X = 0\} = 0.9\) \(\quad \blacksquare\)
由于具有参数 \((n,p)\) 的二项随机变量 \(X\) 表示 \(n\) 个独立试验中的成功次数，其中每个试验成功的概率为 \(p\)，因此我们可以将 \(X\) 表示为：
\[ X = \sum_{i=1}^{n}{X_i} \tag{5.3}\]
其中，\(X_i = \begin{cases} 1, \quad & 第 i 次试验是成功的 \\ 0, \quad & 其它 \end{cases}\)
因为 \(X_i\) 之间是相互独立的伯努利随机变量，因此有：
\(E[X_i] = P\{X_i = 1\} = p\)
\(\textup{Var}(X_i) = E[X_i^2] - E^2[X_i] = p - p^2 = p(1-p)\)，其中因为 \(X_i^2 = X_i\)，所以 \(E[X_i^2] = E[X_i] = p\)。
根据 式 5.3，二项随机变量 \(X\) 的期望和方差为：
\(E[X] = \sum_{i=1}^{n}{E[X_i]} = np\)
\(\textup{Var}(X) = \sum_{i=1}^{n}{\textup{Var}(X_i)} = np(1-p)\)
如果 \(X_1\) 和 \(X_2\) 是两个独立的二项随机变量，并且其参数分别为 \((n_i, p),i=1,2\)，则 \(X_1 + X_2\) 也是一个二项随机变量并且其参数为 \((n_1 + n_2, p)\)。因为 \(X_i,i=1,2\) 代表在 \(n_i\) 个独立试验（每个试验的成功概率为 \(p\)）中成功的数量，所以 \(X_1+X_2\) 代表 \(n_1+n_2\) 个独立试验（每个试验的成功概率为 \(p\)）中成功的数量。因此，\(X_1+X_2\) 是参数为 \((n_1+n_2, p)\) 的二项随机变量。
5.1.1 使用 R 计算二项随机变量的概率
在 R 中，如果想得到参数为 \((n,p)\) 的二项随机变量成功 \(i\) 次的概率，则可以输入：
> dbinom(i, n, p)对于相同的随机变量，如果想得到成功小于或等于 \(i\) 次的概率，则可以输入：
> pbinom(i, n, p)换句话说，如果 \(X\) 是一个二项随机变量，其参数为 \((n,p)\)，则在 R 中：
dbinom(i, n, p) returns P(X = i)
pbinom(i, n, p) returns P(X <= i)习题 5.5 如果 \(X\) 是一个参数为 \((100,0.75)\) 的二项随机变量，计算 \(P(X=70)\) 和 \(P(X \ge 80)\)？
解 5.5. \(P(X=70)\) 的计算代码为：
> dbinom(70, 100, 0.75)\(P(X \ge 80) = 1 - P(X \le 79)\)，其计算代码为：
1 - pbinom(79, 100, 0.75)代码
1 - pbinom(79, 100, 0.75)[1] 0.1488311\(\blacksquare\)
我们还可以使用 R 来绘制二项随机变量的概率图。假设 \(X\) 是一个参数为 \((10, 4)\) 的二项随机变量，并且我们想要绘制 \(P(X=i), i=1...10\) 的概率图。我们可以使用如下的代码：
- 1
- \(i\) 从 0 到 10 并且步长为 1
- 2
- 对于 \(i\) 的每一个值，计算其 \(X=i\) 时的二项随机变量的概率
- 3
-
利用
plot(i, p)画散点图
利用如上的代码，我们可以得到如下的散点图：
代码
i <- seq(0, 10, 1)
p <- dbinom(i, 10, 0.4)
plot(i, p)