方差 \(\sigma^2\) 已知的场景
\(X_1, \dots, X_n\) 是从未知均值 \(\mu\) 且方差为 \(\sigma^2\) 的正态分布总体中抽取的大小为 \(n\) 的样本,假设我们要对以下的原假设进行检验:
\(\begin{align} H_0: \mu = \mu_0 \quad vs \quad H_1: \mu \neq \mu_0 \end{align}\)
其中 \(\mu_0\) 是某个特定的常数。
由于 \(\overline{X} = \frac{1}{n} \sum_{i=1}^n X_i\) 是 \(\mu\) 的点估计量,因此如果 \(\overline{X}\) 与 \(\mu_0\) 相差不大,则接受 \(H_0\) 是合理的。也就是说,检验的 临界区 为:
\[
C = \{ X_1, \dots, X_n : |\overline{X} - \mu_0| > c \}
\tag{8.2}\]
其中 \(c\) 为某个合适的值。
如果我们要求检验的显著性水平为 \(\alpha\) ,我们必须确定 式 8.2 中的临界值 \(c\) ,以使得 I 类错误等于 \(\alpha\) 。即,\(c\) 必须满足:
\[
P_{\mu_0}\{ |\overline{X} - \mu_0| > c \} = \alpha
\tag{8.3}\]
\(P_{\mu_0}\) 表示我们在 \(\mu = \mu_0\) 的假设下计算 式 8.3 的概率。然而,当 \(\mu = \mu_0\) 时,\(\overline{X}\) 将服从均值为 \(\mu_0\) 且方差为 \(\sigma^2/n\) 的正态分布,因此 式 8.4 定义的 \(Z\) 将服从标准正态分布。
\[
Z \equiv \frac{\overline{X} - \mu_0}{\sigma/\sqrt{n}} = \sqrt{n} \frac{(\overline{X} - \mu_0)}{\sigma}
\tag{8.4}\]
于是,式 8.3 等价于:
\(P\left\{ |Z| > \frac{c \sqrt{n}}{\sigma} \right\} = \alpha\)
即:
\(2P\left\{ Z > \frac{c \sqrt{n}}{\sigma} \right\} = \alpha\)
其中 \(Z\) 是标准正态分布随机变量。然而,我们知道
\(P\{ Z > z_{\alpha/2} \} = \alpha/2\)
因此:
\(\frac{c \sqrt{n}}{\sigma} = z_{\alpha/2}\)
即:
\(c = \frac{z_{\alpha/2} \sigma}{\sqrt{n}}\)
因此,显著性水平为 \(\alpha\) 的检验为:
如果 \(\frac{\sqrt{n}}{\sigma} |\overline{X} - \mu_0| > z_{\alpha/2}\) ,则拒绝 \(H_0\) ;
否则,接受 \(H_0\) 。
\[
\begin{align}
\text{拒绝} H_0 &: \quad \frac{\sqrt{n}}{\sigma} |\overline{X} - \mu_0| > z_{\alpha/2} \\
\text{接受} H_0 &: \quad \frac{\sqrt{n}}{\sigma} |\overline{X} - \mu_0| \le z_{\alpha/2}
\end{align}
\tag{8.5}\]
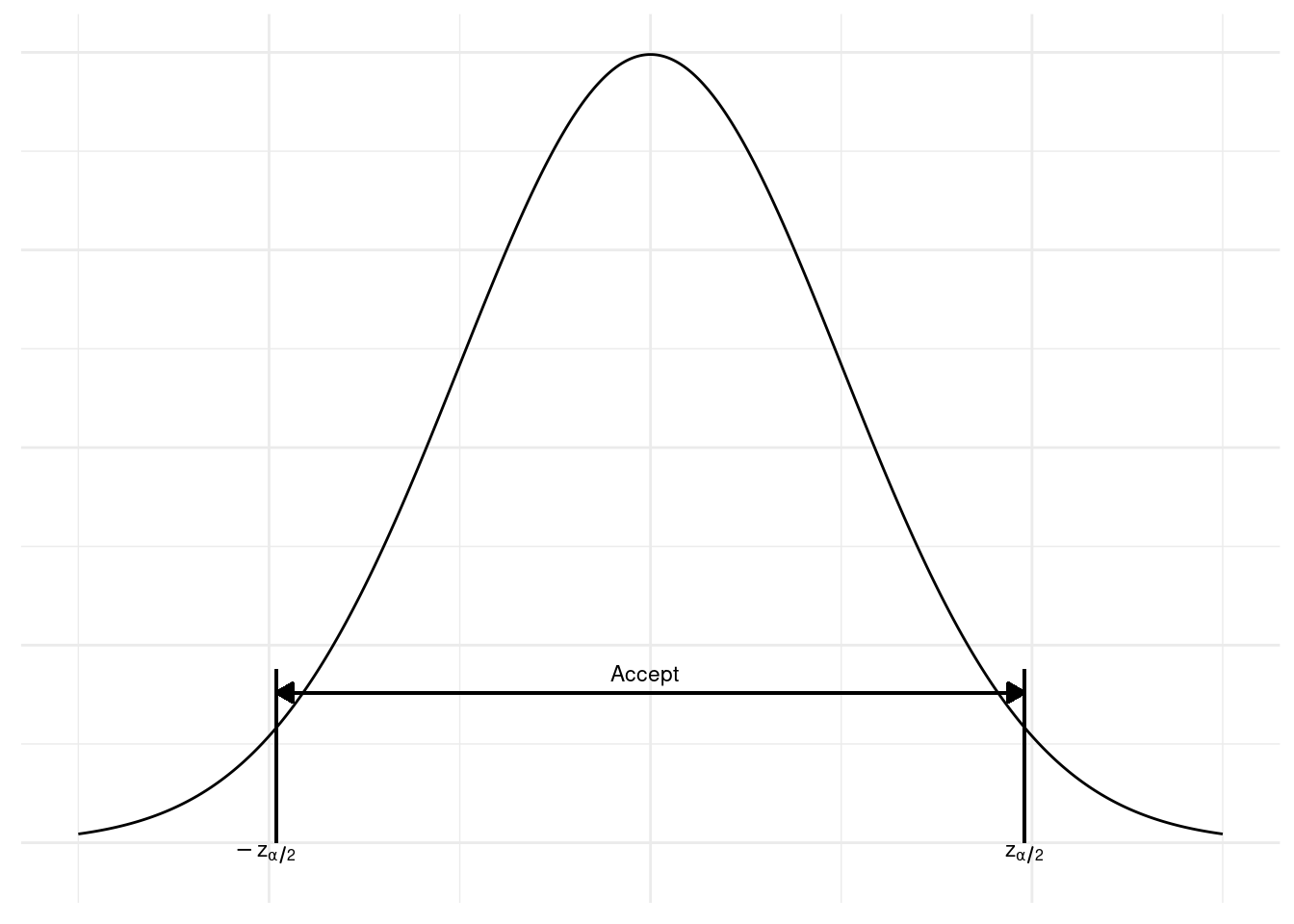
可以通过图 图 8.1 来直观地表示 式 8.5 ,在 图 8.1 中,我们叠加了标准正态分布的概率密度函数(即当 \(H_0\) 成立时,统计量 \(\sqrt{n}(\overline{X} - \mu_0)/\sigma\) 的概率密度)。
代码
library (latex2exp)library (ggplot2)<- seq (- 3 , 3 , 0.01 ) <- dnorm (x)<- data.frame (x= x, y= y)ggplot (df, aes (x= x, y= y)) + geom_line () + geom_segment (x= - 1.96 , y= dnorm (- 1.96 ) * 1.5 , xend= - 1.96 , yend= 0 ) + geom_segment (x= 1.96 , y= dnorm (1.96 ) * 1.5 , xend= 1.96 , yend= 0 ) + geom_segment (x= - 1.96 , y= dnorm (- 1.96 ) * 1.3 , xend= 1.96 , yend= dnorm (1.96 ) * 1.3 , arrow = arrow (ends = "both" , type = "closed" , length = unit (0.1 , "inches" ))) + annotate ("text" , x = - 1.86 , y = - 0.01 , label = TeX ("$-z_{ \\ alpha/2}$" ), hjust = 1 , vjust = 0 , size = 3 ) + annotate ("text" , x = 2.06 , y = - 0.01 , label = TeX ("$z_{ \\ alpha/2}$" ), hjust = 1 , vjust = 0 , size = 3 ) + annotate ("text" , x = 0.15 , y = dnorm (- 1.96 ) * 1.4 , label = "Accept" , hjust = 1 , vjust = 0 , size = 3 ) + theme_minimal () + theme (axis.text = element_blank (),axis.title = element_blank ())
习题 8.1 习题 7.7 类似,假设从 A 地发射一个信号 \(\mu\) 到 B 地,在 B 接收到的信号的值服从均值为 \(\mu\) 、方差为 4 的正态分布。也就是说,B 地接收到的信号会加入随机噪声、并且该随机噪声是服从 \(\mathcal{N}(0, 4)\) 的随机变量。现在,B 地的人怀疑今天 A 地发送的信号值为 \(\mu = 8\) 。假设 A 地独立发送了 5 次该信号,且在 B 地接收到的信号的平均值为 \(\overline{X} = 9.5\) 。请对 今天 A 地发送的信号值为 \(\mu = 8\) 这一假设进行检验。
习题 8.2
\(\frac{\sqrt{n}}{\sigma} |\overline{X} - \mu_0| = \frac{\sqrt{5}}{2} (1.5) = 1.68\)
由于 1.68 小于 \(z_{0.025} = 1.96\) ,因此应该接受该假设。换句话说,因为当 A 地发射的信号真的为 8 时,那么会有 5% 的可能性发生像我们观察到的样本平均值偏离 8 的这种情况,但是这个比例并没有达到足以令我们拒绝原假设,所以观察到的数据与原假设并不矛盾。但是,如果我们选择了更不严格的显著性水平——比如 \(\alpha = 0.1\) ,此时,因为 1.68 大于 \(z_{0.05} = 1.645\) ,那么我们将拒绝原假设。因此,如果我们选择了 10% 的概率会错误的拒绝原假设的情况下(第 I 类错误 ),那么我们将拒绝原假设。
选择合适的显著性水平(\(\alpha\) )并不是一个一成不变的标准,而是需要根据具体情况进行调整。例如,如果错误的拒绝实际为真的原假设 \(H_0\) 会导致巨大损失,那么我们可能会选择非常保守的显著性水平,此时可以选择 0.05 或 0.01 的显著性水平。此外,如果我们一开始就非常相信 \(H_0\) 是正确的,那么我们就需要设置一个非常严格的标准并要求有强有力的数据证据才能认为 \(H_0\) 是错误的。也就是说,在这种情况下,我们通常需要设置一个非常低的显著性水平(例如 0.01 或者更低)。\(\blacksquare\)
式 8.5 给出的 检验 的描述如下:对于检验统计量 \(\sqrt{n}|\overline{X} - \mu_0|/\sigma\) 的任何观测值——我们称其为 \(v\) ——当 \(H_0\) 成立时,如果检验统计量大于或等于 \(v\) 的概率小于或等于显著性水平 \(\alpha\) ,则 检验 说明需要拒绝原假设 \(H_0\) 。
由此,我们可以通过以下步骤来确定是否接受原假设 \(H_0\) :
首先,计算检验统计量的值 \(v\) ;
其次,计算标准正态分布(取绝对值)的概率,即标准正态分布中大于 \(v\) 的概率,我们称这一概率为检验的 \(p-\text{value}\) 。\(p-\text{value}\) 给出了临界显著性水平的意义,即如果 \(p-\text{value}\) 大于显著性水平 \(\alpha\) ,则接受 \(H_0\) ;如果 \(p-\text{value}\) 小于或等于显著性水平 \(\alpha\) ,则拒绝 \(H_0\) 。
在实际操作中,显著性水平往往不是预先设定的,而是会首先通过观察数据来确定 \(p-\text{value}\) 。
有时,\(p-\text{value}\) 会明显大于我们愿意使用的任何显著性水平,因此我们可以非常轻松的就接受原假设 \(H_0\) 。
而有时,\(p-\text{value}\) 值又非常小(甚至小于任何我们会使用到的显著性水平),因此显然我们应该拒绝该假设。
例 8.1 习题 8.2 中,假设接收到的 5 个值的平均值为 \(\overline{X} = 8.5\) 。在这种情况下,
\(\frac{\sqrt{n}}{\sigma} |\overline{X} - \mu_0| = \frac{\sqrt{5}}{4} = 0.559\)
因为
\(P\{|Z| > 0.559\} = 2P\{Z > 0.559\}= 2 \times 0.288 = 0.576\)
所以 \(p-\text{value}\) 为 0.576,因此信号值为 8 的原假设在任何显著性水平 \(\alpha < 0.576\) 下都将被接受。显然,我们绝不会使用一个高达 0.576 的显著性水平来检验原假设,因此我们将接受 \(H_0\) 。
另一方面,如果数据的平均值为 11.5,则检验均值为 8 的 \(p-\text{value}\) 值将为
\(P\{|Z| > 1.75\sqrt{5}\} = P\{|Z| > 3.913\} \approx 0.00005\)
对于如此小的\(p-\text{value}\) ,我们将拒绝信号值为 8 的原假设。\(\blacksquare\)
到现在为止,我们还没有讨论过 第 II 类错误 的概率——也就是在真实均值 \(\mu\) 不等于 \(\mu_0\) 时错误的接受原假设的概率。第 II 类错误 的概率取决于 \(\mu\) 的值,因此我们定义 \(\beta(\mu)\) 如下:
\(\begin{align}\beta(\mu) &= P_\mu\{\text{接受 } H_0\} \\ &=P_{\mu}\left\{\left|\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\right| \le z_{\alpha/2}\right\} \\ &=P_{\mu}\left\{-z_{\alpha/2} \le \frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\le z_{\alpha/2}\right\} \end{align}\)
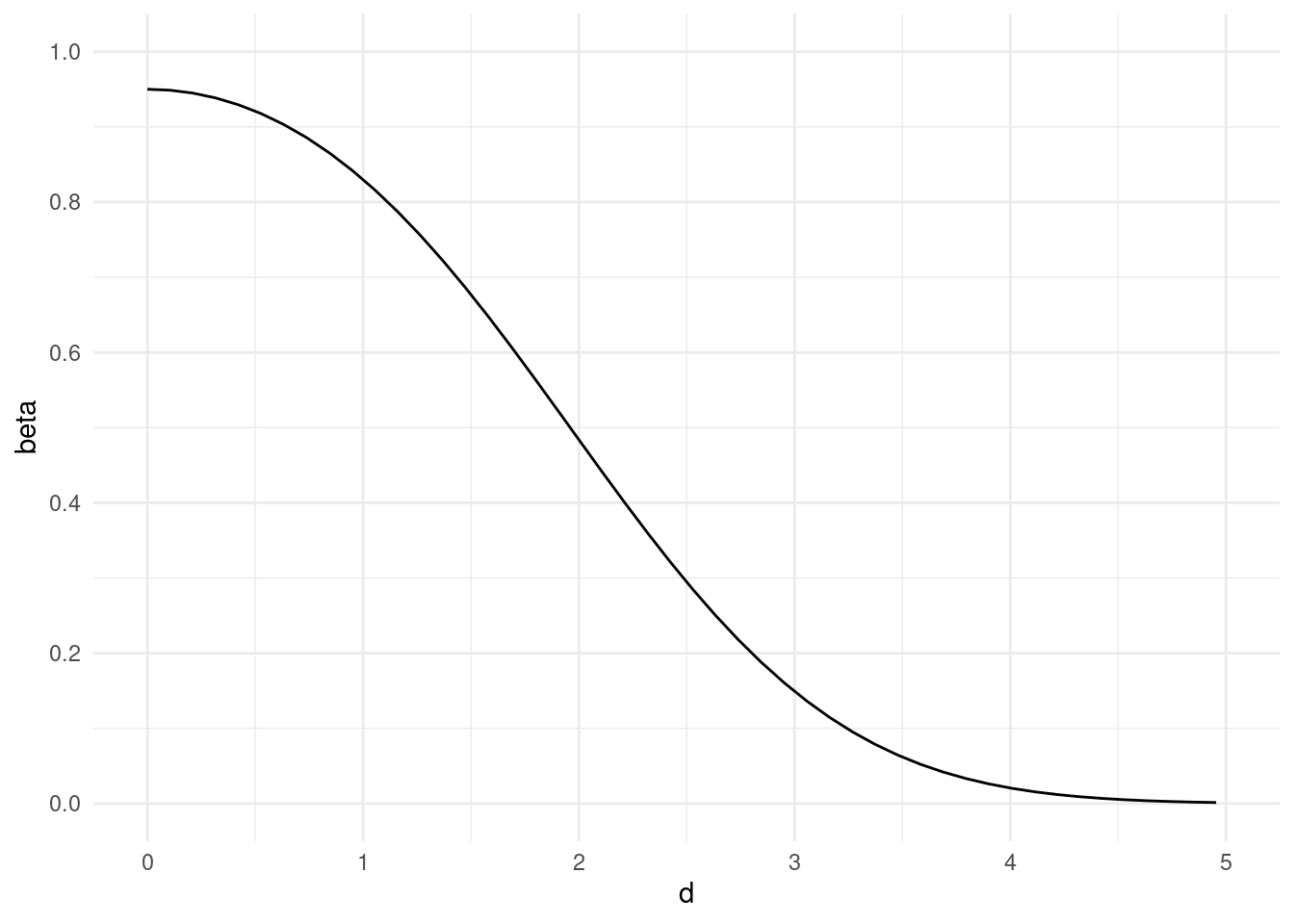
我们称函数 \(\beta(\mu)\) 为 Operating Characteristic (OC )Curve,\(\beta(\mu)\) 表示当真实均值为 \(\mu\) 时接受原假设 \(H_0\) 的概率。
为了计算这个概率,我们使用 \(\overline{X}\) 服从均值为 \(\mu\) 、方差为 \(\sigma^2/n\) 的正态分布的事实,因此
\(Z \equiv \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim \mathcal{N}(0, 1)\)
因此,
\[
\begin{align}
\beta(\mu) &= P_\mu\left\{-z_{\alpha/2} \leq \frac{\overline{X} - \mu_0}{\sigma/\sqrt{n}} \leq z_{\alpha/2}\right\} \\
&= P_\mu\left\{-z_{\alpha/2} \leq \frac{\overline{X} - \mu + \mu - \mu_0}{\sigma/\sqrt{n}} \leq z_{\alpha/2}\right\} \\
&= P_\mu\left\{-z_{\alpha/2} - \frac{\mu}{\sigma / \sqrt{n}} \leq \frac{\overline{X} - \mu - \mu_0}{\sigma/\sqrt{n}} \leq z_{\alpha/2} - \frac{\mu}{\sigma / \sqrt{n}} \right\} \\
&= P_\mu\left\{ -z_{\alpha/2} - \frac{\mu}{\sigma / \sqrt{n}} \leq Z - \frac{\mu_0}{\sigma/\sqrt{n}} \leq z_{\alpha/2} - \frac{\mu}{\sigma / \sqrt{n}} \right\} \\
&= P\left\{\frac{\mu_0 - \mu}{\sigma / \sqrt{n}} - z_{\alpha/2} \le Z \le \frac{\mu_0 - \mu}{\sigma / \sqrt{n}} + z_{\alpha/2}\right\} \\
&= \Phi\left(\frac{\mu_0 - \mu}{\sigma/\sqrt{n}} + z_{\alpha/2}\right) - \Phi\left(\frac{\mu_0 - \mu}{\sigma/\sqrt{n}} - z_{\alpha/2}\right)
\end{align}
\tag{8.6}\]
其中 \(\Phi\) 是标准正态分布函数。
对于固定的显著性水平 \(\alpha\) ,由 式 8.6 给出的 OC 曲线是关于 \(\mu_0\) 对称的,并且实际上仅通过 \(\sqrt{n}|\mu - \mu_0|/\sigma\) 而依赖于 \(\mu\) 。当 \(\alpha = 0.05\) 时,这条曲线的横坐标由 \(\mu\) 改为 \(d = \sqrt{n}|\mu - \mu_0|/\sigma\) ,并且曲线如 图 8.2 所示。
代码
library (ggplot2)# β(μ) 的计算函数 <- function (mu, mu0, sigma, n, alpha) {= qnorm (1 - alpha / 2 )= sqrt (n) * (mu0 - mu) / sigma= pnorm (d + z_alpha) - pnorm (d - z_alpha)return (beta)# 参数设置 <- 0 # 原假设的均值 <- 3 # 标准差 <- 10 # 样本大小 <- 0.05 # 显著性水平 # 生成一系列 μ 的值 <- seq (- 5 , 5 , by = 0.1 )# 计算每个 μ 对应的 β(μ) <- sapply (mu_values, calculate_beta, mu0 = mu0, sigma = sigma, n = n, alpha = alpha)<- sqrt (n) / sigma * abs (mu0 - mu_values)# 创建数据框用于绘图 <- data.frame (mu = mu_values, d = d, beta = beta_values)# 绘制 OC 曲线 ggplot (df, aes (x = d, y = beta)) + geom_line () + scale_x_continuous (limits = c (0 , 5 )) + scale_y_continuous (limits = c (0 , 1 ), breaks = seq (0 , 1 , 0.2 )) + theme_minimal ()
例 8.2 习题 8.2 中的问题,当实际发送的值为 10 时,计算接受原假设 \(\mu = 8\) 的概率?
# β(μ) 的计算函数 <- function (mu, mu0, sigma, n, alpha) {= qnorm (1 - alpha / 2 )= sqrt (n) * (mu0 - mu) / sigma= pnorm (d + z_alpha) - pnorm (d - z_alpha)return (beta)<- calculate_beta (10 , 8 , 2 , 5 , 0.05 )
\(\blacksquare\)
我们称 \(1 - \beta(\mu)\) 为 检验功效函数 (power-function of the test )。因此,对于给定的 \(\mu\) 值,检验功效 等于当 \(\mu\) 为真实值时拒绝原假设的概率。
在确定所需的随机样本大小以满足我们对 第 II 类错误 的某些特定要求的场景下,Operating Characteristic 函数非常有用。例如,假设我们希望确定所需的样本大小 \(n\) ,以确保当真实均值实际上为 \(\mu_1\) 时,接受原假设 \(H_0: \mu = \mu_0\) 的概率大约为 \(\beta\) 。也就是说,我们希望找到 \(n\) 使得:
\(\beta(\mu_1) \approx \beta\)
但是,根据 式 8.6 ,我们可以推导出,如上的式子等价于
\[
\Phi \left(\frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} + z_{\alpha/2}\right) - \Phi \left(\frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} - z_{\alpha/2}\right) \approx \beta \quad
\tag{8.7}\]
尽管无法直接对 式 8.7 进行求解并得到 \(n\) ,但可以使用标准正态分布表来求解得到 \(n\) 。此外,还可以通过 式 8.7 推导出 \(n\) 的近似值 式 8.9 。
首先,假设 \(\mu_1 > \mu_0\) ,于是这意味着:
\(\frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} - z_{\alpha/2} \leq -z_{\alpha/2}\)
由于 \(\Phi\) 是一个递增函数,因此:
\(\Phi \left(\frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} - z_{\alpha/2}\right) \leq \Phi(-z_{\alpha/2}) = P\{Z \leq -z_{\alpha/2}\} = P\{Z \geq z_{\alpha/2}\} = \alpha/2\)
因此,我们可以取
\(\Phi \left(\frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} - z_{\alpha/2}\right) \approx 0\)
根据 式 8.7 可以得到:
\[
\beta \approx \Phi \left(\frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} + z_{\alpha/2}\right)
\tag{8.8}\]
或者,由于
\(\beta = P\{Z > z_{\beta}\} = P\{Z < -z_{\beta}\} = \Phi(-z_{\beta})\)
根据 式 8.8 得到:
\(-z_{\beta} \approx \frac{\sqrt{n}(\mu_0 - \mu_1)}{\sigma} + z_{\alpha/2}\)
即:
\[
n \approx \frac{(z_{\alpha/2} + z_{\beta})^2 \sigma^2}{(\mu_1 - \mu_0)^2}
\tag{8.9}\]
事实上,当 \(\mu_1 < \mu_0\) 时,我们会得到近似相同的结果(留作习题),因此,在任何情况下 式 8.9 都是如下场景的一个合理的近似值:
估计所需的样本大小,以确保当真实均值为 \(\mu = \mu_1\) 时,第 II 类错误 的概率大约等于 \(\beta\) 。
习题 8.3 习题 8.2 的问题,在 0.05 的显著性水平下,当 \(\mu\) 实际为 9.2 时,需要发送多少次信号才能使得原假设 \(H_0: \mu = 8\) 至少有 75% 的概率被拒绝?
解 8.1 . \(z_{.025} = 1.96\) ,\(z_{0.25} = .67\) ,根据 式 8.9 有:
\(n \approx \frac{(1.96 + 0.67)^2}{(1.2)^2} 4 \approx 19.21\)
因此需要一个大小为 20 的样本。
根据方程 式 8.6 ,当 \(n = 20\) 时,
\(\begin{align} \beta(9.2) &= \Phi \left(-\frac{1.2\sqrt{20}}{2} + 1.96\right) - \Phi \left(-\frac{1.2\sqrt{20}}{2} - 1.96\right) \\ & \approx \Phi(-0.723) - \Phi(-4.643) \\ & \approx 1 - \Phi(0.723) \\ & \approx 0.235 \end{align}\)
# β(μ) 的计算函数 <- function (mu, mu0, sigma, n, alpha) {= qnorm (1 - alpha / 2 )= sqrt (n) * (mu0 - mu) / sigma= pnorm (d + z_alpha) - pnorm (d - z_alpha)return (beta)<- calculate_beta (9.2 , 8 , 2 , 20 , 0.05 )
因此,如果发送消息 20 次,那么当真实均值为 9.2 时,有 76.5% 的概率会拒绝原假设 \(\mu = 8\) 。\(\blacksquare\)
单边检验
在检验原假设 \(\mu = \mu_0\) 时,我们选择了一种检验以使得在 \(\overline{X}\) 远离 \(\mu_0\) 时拒绝原假设。也就是说,和 \(\mu_0\) 相比,\(\overline{X}\) (\(\mu\) 的估计量)的一个非常小的值或非常大的值似乎使得 \(\mu\) 不可能等于 \(\mu_0\) 。然而,当 \(\mu\) 等于 \(\mu_0\) 的唯一 备择假设 是 \(\mu > \mu_0\) 时会发生什么呢?也就是说,当 备择假设 为 \(H_1: \mu > \mu_0\) 时会发生什么?显然,此时,在 \(\overline{X}\) 很小(与 \(\mu\) 相比)时,\(H_0\) 为真比 \(H_1\) 为真更有可能发生。因此,此时,我们不希望拒绝 \(H_0\) 。
因此,对于 式 8.10 的检验
\[
H_0: \mu = \mu_0 \quad vs. \quad H_1: \mu > \mu_0
\tag{8.10}\]
当 \(\mu_0\) 的点估计 \(\overline{X}\) 远大于 \(\mu_0\) 时,我们应该拒绝 \(H_0\) 。这意味着,临界区 应如下所示:
\(C = \{(X_1, \dots, X_n) : \overline{X} - \mu_0 > c\}\)
由于当 \(H_0\) 为真时,拒绝原假设的概率应该等于 \(\alpha\) ,因此 \(c\) 需要满足:
\[
P_{\mu_0}\{\overline{X} - \mu_0 > c\} = \alpha
\tag{8.11}\]
当 \(H_0\) 为真时,\(Z\) 服从标准正态分布:
\(Z = \frac{\overline{X} - \mu_0}{\sigma/\sqrt{n}} = \sqrt{n}\frac{(\overline{X} - \mu_0)}{\sigma}\)
所以,式 8.11 等价于:
\(P\left\{Z > \frac{c\sqrt{n}}{\sigma}\right\} = \alpha\)
由于
\(P\{Z > z_{\alpha}\} = \alpha\)
所以有:
\[
c = \frac{z_{\alpha}\sigma}{\sqrt{n}}
\tag{8.12}\]
因此,假设 式 8.10 的检验是当 \(\overline{X} - \mu_0 > z_{\alpha} \sigma / \sqrt{n}\) 时拒绝 \(H_0\) ,否则接受 \(H_0\) 。即:
\[
\begin{align}
&\text{接受} \ H_0 \quad \text{如果} \frac{\sqrt{n}}{\sigma} (\overline{X} - \mu_0) \leq z_{\alpha} \\
&\text{拒绝} \ H_0 \quad \text{如果} \frac{\sqrt{n}}{\sigma} (\overline{X} - \mu_0) \gt z_{\alpha} \\
\end{align}
\tag{8.13}\]
因为仅在 \(\overline{X}\) 较大时才会拒绝原假设,所以 式 8.13 称之为 单边临界区域 (one-sided critical region )。相应地,与 备择假设 为 \(H_1: \mu \neq \mu_0\) 的双边检验问题相比,式 8.14 所示的假设检验问题也称之为 单边检验问题 。
\[
\begin{align}
H_0: &\mu = \mu_0 \\
H_1: & \mu > \mu_0
\end{align}
\tag{8.14}\]
为了计算 单边检验 中的 \(p-\text{value}\) ,我们
首先使用观测数据确定统计量 \(\frac{\sqrt{n}(\overline{X} - \mu_0)}{\sigma}\) 的值。
然后,\(p-\text{value}\) 等于标准正态分布中大于等于该值的概率。
习题 8.4 习题 8.2 中,我们预先知道信号值至少是 8,那么在这种情况下可以得出什么结论?
解 8.2 .
\(\begin{align}H_0: &\mu = 8 \\ H_1: &\mu > 8 \end{align}\)
单边检验统计量的值为:
\(\sqrt{n} \frac{(\overline{X} - \mu_0)}{\sigma} = \sqrt{5} \frac{(9.5 - 8)}{2} = 1.68\)
并且 \(p-\text{value}\) 为标准正态分布超过 1.68 的概率,即
\(p-\text{value} = 1 - \Phi(1.68) = 0.0465\)
该检验将在所有大于或等于 0.0465 的显著性水平下拒绝原假设。例如,如果显著性水平 \(\alpha = 0.05\) ,那么我们将拒绝原假设。 \(\blacksquare\)
式 8.13 所示的单边检验的 Operating Characteristic 函数 \(\beta(\mu) = P_{\mu}\{\text{接受} H_0\}\) 为:
\(\begin{align} \beta(\mu) &= P_{\mu}\left\{ \overline{X} \leq \mu_0 + z_{\alpha}\frac{\sigma}{\sqrt{n}} \right\} \\ &= P\left\{ \frac{\sqrt{n}(\overline{X} - \mu_0)}{\sigma} \leq \frac{\sqrt{n}(\mu_0 - \mu)}{\sigma} + z_{\alpha} \right\} \\ &= P\left\{ Z \leq \frac{\sqrt{n}(\mu_0 - \mu)}{\sigma} + z_{\alpha} \right\}, \quad Z \sim N(0, 1) \end{align}\)
即:
\(\beta(\mu) = \Phi \left( \frac{\sqrt{n}(\mu_0 - \mu)}{\sigma} + z_{\alpha} \right)\)
由于 \(\Phi\) 是概率分布函数,因此 \(\Phi\) 随着自变量的增加而递增,所以从直觉而言:\(\beta(\mu)\) 随 \(\mu\) 的增加而减少是合理的。显然,当真实均值 \(\mu\) 越大时,\(\mu \leq \mu_0\) 的可能性就越小。此外,由于 \(\Phi(z_{\alpha}) = 1 - \alpha\) ,因此
\(\beta(\mu_0) = 1 - \alpha\)
最初用于检验 \(H_0: \mu = \mu_0 \ vs. \ H_1: \mu > \mu_0\) 的 式 8.13 也可以用于:在显著性水平 \(\alpha\) 下,如下假设的单边检验:
\[
H_0: \mu \leq \mu_0 \quad vs. \quad H_1: \mu > \mu_0
\tag{8.15}\]
为了验证它仍然是在显著性水平为 \(\alpha\) 下的检验,我们需要证明:当 \(H_0\) 为真时,拒绝原假设的概率不超过 \(\alpha\) 。也就是说,我们必须验证:
\(1 - \beta(\mu) \leq \alpha , \quad \quad \forall \mu \leq \mu_0\)
或者
\(\beta(\mu) \geq 1 - \alpha , \quad \quad \forall \mu \leq \mu_0\)
之前已经证明,对于由方程 式 8.13 给出的检验,\(\beta(\mu)\) 随 \(\mu\) 的增加而减少,且 \(\beta(\mu_0) = 1 - \alpha\) 。于是:
\(\beta(\mu) \geq \beta(\mu_0) = 1 - \alpha , \quad \quad \forall \mu \leq \mu_0\)
这表明由 式 8.13 给出的检验在显著性水平 \(\alpha\) 下,对 \(H_0: \mu \leq \mu_0 \quad vs. \quad H_1: \mu > \mu_0\) 仍然是一个 显著性水平为 \(\alpha\) 的检验。
我们还可以在在显著性水平 \(\alpha\) 下对如下的假设
\(H_0: \mu = \mu_0 \quad (\text{或} \quad \mu \geq \mu_0) \quad vs \quad H_1: \mu < \mu_0\)
做出如下的单边检验:
\(\begin{align} \text{接受 } H_0, & \quad \text{如果} \quad \frac{\sqrt{n}}{\sigma}(\overline{X} - \mu_0) \geq -z_{\alpha} \\ \text{拒绝 } H_0, & \quad \text{其他} \end{align}\)
可以通过首先计算检验统计量 \(\frac{\sqrt{n}(\overline{X} - \mu_0)}{\sigma}\) 来进行该检验。\(p-\text{value}\) 等于标准正态分布小于 \(\frac{\sqrt{n}(\overline{X} - \mu_0)}{\sigma}\) 的概率,当 \(p-\text{value}\) 小于任何的显著性水平时,我们将拒绝原假设。
习题 8.5
注意 :如上问题中有一个问题,即我们如何事先知道标准差为 0.8。一个可能性是,香烟尼古丁含量的变化源自每支香烟中的烟草量的变化,而不是使用的处理方法。因此,可以从以往的经验中得知香烟中尼古丁含量的标准差。
解 8.3 . \(\alpha\) 的检验。因此,拒绝原假设是对数据与此假设不一致的强烈陈述,而当接受原假设时,并不能做出类似的陈述。因此,我们希望仅在有充分证据支持生产商的说法时才能接受生产商的说法,因此我们应将生产商的说法作为备择假设。也就是说,我们应该检验:
\(H_0: \mu \geq 1.6 \quad vs \quad H_1: \mu < 1.6\)
此时,检验统计量的值为
\(\frac{\sqrt{n}(\overline{X} - \mu_0)}{\sigma} = \frac{\sqrt{20}(1.54 - 1.6)}{0.8} = -0.336\)
因此,\(p\) 值为
\(\text{p-value} = P\{Z < -0.336\} = 0.368\)
由于 \(\text{p-value}\) 大于 0.05,因此在显著性水平为 5% 的情况下,样本数据不足以拒绝平均尼古丁含量超过 1.6 毫克的假设。换句话说,尽管样本数据支持了香烟生产商的说法,但尚不足以证明应该接受生产商的说法。 \(\blacksquare\)
置信区间估计 与 假设检验 之间有直接的类比关系。例如,对于均值为 \(\mu\) 、方差为 \(\sigma^2\) (已知)的正态分布总体,正如我们在 小节 7.3 \(\mu\) 的 \(100(1 - \alpha)\%\) 置信区间为:
\(\mu \in \left( \overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}}, \, \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right)\)
其中 \(\overline{X}\) 是观测到的样本均值。更正式地,前述置信区间等价于:
\(P \left\{ \mu \in \left( \overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}}, \, \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right) \right\} = 1 - \alpha\)
因此,如果 \(\mu = \mu_0\) ,则 \(\mu_0\) 落在区间
\(\left( \overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}}, \, \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right)\)
的概率是 \(1 - \alpha\) ,这意味着显著性水平为 \(\alpha\) 的假设——\(H_0: \mu = \mu_0 \quad vs \quad H_1: \mu \neq \mu_0\) 的检验是:
当 \(\mu_0 \notin \left( \overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}}, \, \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right)\) 时拒绝 \(H_0\) 。
类似地,\(\mu\) 的 \(100(1 - \alpha)\%\) 单边置信区间由下式给出:
\(\mu \in \left( \overline{X} - z_{\alpha}\frac{\sigma}{\sqrt{n}}, \, \infty \right)\)
因此,显著性水平为 \(\alpha\) 的假设——\(H_0: \mu \leq \mu_0 \quad vs \quad H_1: \mu > \mu_0\) 的检验是:
当 \(\mu_0 \notin \left( \overline{X} - z_{\alpha}\frac{\sigma}{\sqrt{n}}, \, \infty \right)\) (即,\(\mu_0 < \overline{X} - z_{\alpha}\frac{\sigma}{\sqrt{n}}\) ) 时拒绝 \(H_0\) 。
关于稳健性(robustness )的说明 :统计检验通常基于一些前提条件或假设(例如样本来自正态分布、方差是已知的等),当这些前提条件或假设并不满足的时候,某个检验仍能有良好的表现,那么我们认为该检验是稳健(robust )的。例如,小节 8.3.1 小节 8.3.1.1 \(\sigma^2\) 的正态分布。然而,在推导这些检验时,这个假设仅用于得出:\(\overline{X}\) 也服从正态分布。但是,由中心极限定理(定理 6.1 )可知,当样本量足够大时,无论总体服从什么分布,\(\overline{X}\) 都将近似服从正态分布。因此,我们可以得出结论,这些检验对于任何方差为 \(\sigma^2\) 的总体分布都将是相对稳健的。
表 8.1 对本节的假设检验进行了总结。
方差未知的场景:\(t-\text{检验}\)
到目前为止,我们假设正态分布总体的唯一未知参数是其均值。然而,更常见的情况是均值 \(\mu\) 和方差 \(\sigma^2\) 都未知。假设在这种情况下,再次考虑检验均值等于某个指定值 \(\mu_0\) 的假设。即考虑以下假设检验:
\(H_0: \mu = \mu_0 \quad vs \quad H_1: \mu \neq \mu_0\)
需要注意的是,此时,因为我们并没有有指定 \(\sigma^2\) 的值,因此原假设并不是一个 简单假设 (小节 8.2
与 小节 8.3.1 \(\overline{X}\) 远离 \(\mu_0\) 时,拒绝 \(H_0\) 是合理的。然而,样本均值 \(\overline{X}\) 需要远离 \(\mu_0\) 多远才能合理地拒绝 \(H_0\) 取决于方差 \(\sigma^2\) (参见 式 8.4 )。如 式 8.5 ,\(\sigma^2\) 已知时,当 \(|\overline{X} - \mu_0|\) 超过 \(z_{\alpha/2}\sigma/\sqrt{n}\) 时,检验会拒绝 \(H_0\) ,即当:
\(\frac{\sqrt{n}|\overline{X} - \mu_0|}{\sigma} > z_{\alpha/2}\)
时拒绝 \(H_0\) 。
现在,当 \(\sigma^2\) 未知时,需要先估计 \(\sigma^2\) :
\(S^2 = \frac{\sum_{i=1}^{n} (X_i - \overline{X})^2}{n-1}\)
然后,当
\(\frac{|\overline{X} - \mu_0|}{S/\sqrt{n}}\)
较大时拒绝 \(H_0\) 。
为了确定在显著性水平 \(\alpha\) 下, 检验统计量
\(\frac{\sqrt{n}|\overline{X} - \mu_0|}{S}\)
需要大到什么程度时才能拒绝 \(H_0\) ,我们必须确定当 \(H_0\) 为真时该统计量的概率分布。然而,如 小节 6.5 推论 6.1 所述,当 \(\mu = \mu_0\) 时,下式定义的统计量 \(T\) 服从自由度为 \(n-1\) 的 \(t-\text{分布}\) 。
\(T = \frac{\sqrt{n}(\overline{X} - \mu_0)}{S}\)
因此,
\[
P_{\mu_0}\left\{ -t_{\alpha/2, n-1} \leq \frac{\sqrt{n}(\overline{X} - \mu_0)}{S} \leq t_{\alpha/2, n-1} \right\} = 1 - \alpha
\tag{8.16}\]
其中 \(t_{\alpha/2, n-1}\) 是自由度为 \(n-1\) 的 \(t\) 分布在 \(\left (100 \frac{\alpha}{2} \right) \%\) 处的上百分位数。
因此,从 式 8.16 中,我们可以看出,当 \(\sigma^2\) 未知的情况时,在适当的显著性水平 \(\alpha\) 下的
\(H_0: \mu = \mu_0 \quad vs \quad H_1: \mu \neq \mu_0\)
的检验为:
\[
\begin{align}
\text{接受} \ H_0, &\quad \text{如果} \quad \frac{\sqrt{n}|\overline{X} - \mu_0|}{S} \leq t_{\alpha/2, n-1} \\
\text{拒绝} \ H_0, &\quad \text{如果} \quad \frac{\sqrt{n}|\overline{X} - \mu_0|}{S} \gt t_{\alpha/2, n-1}
\end{align}
\tag{8.17}\]
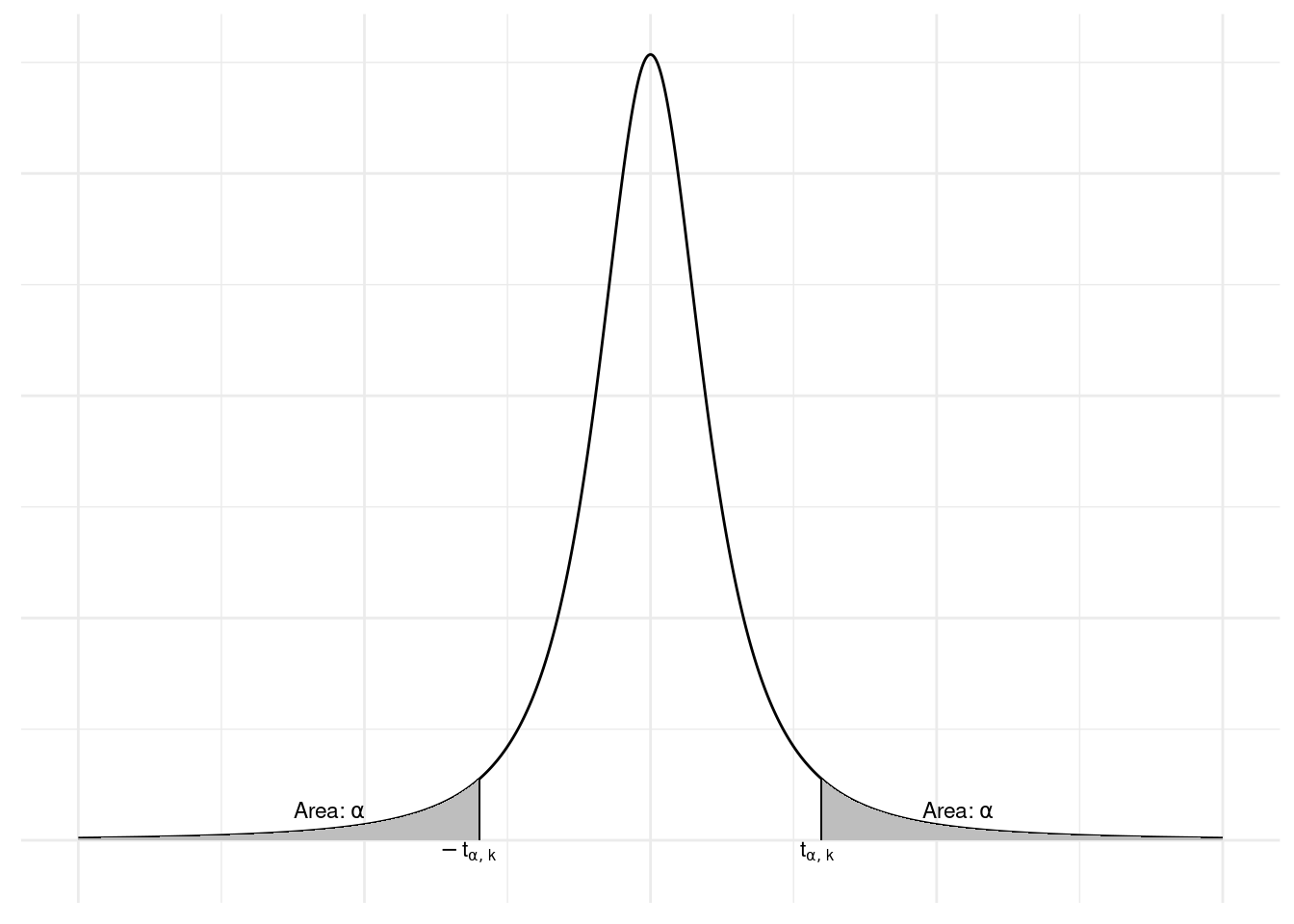
我们称 式 8.17 定义的检验为 双边 \(t-\text{检验}\) (two-sided t-test ),如 图 8.3 所示。
如果我们用 \(t\) 表示检验统计量 \(T = \sqrt{n}(\overline{X} - \mu_0)/S\) 的观察值,那么检验的 \(p-\text{value}\) 是当 \(H_0\) 为真时,\(|T|\) 超过 \(|t|\) 的概率。也就是说,\(p-\text{value}\) 是自由度为 \(n - 1\) 的 \(t-\text{分布}\) 的绝对值超过 \(|t|\) 的概率。因此,检验要求在所有的显著性水平均大于 \(p-\text{value}\) 时拒绝原假设,同时在所有的显著性水平均小于 \(p-\text{value}\) 时接受原假设。
习题 8.6
解 8.4 . \(T-\text{统计量}\) 的值是
\(T = \frac{\sqrt{n} \overline{X}}{S} = \frac{\sqrt{50} \cdot 14.8}{6.4} = 16.352\)
很明显,我们应该拒绝该变化完全是由偶然因素引起的假设。
然而,不幸的是,此时我们还不能得出结论:这些变化是由于特定药物而不是其他因素引起的。例如,众所周知,任何药物(无论该药物是否直接与患者的病痛相关)通常都会导致患者病情的改善——即所谓的 安慰剂效应 (placebo effect )。此外,另一个需要考虑的可能性是测试期间的天气情况,因为可以合理地认为天气会影响血液胆固醇水平。
确实,必须得出结论:上述的实验设计非常不合理。为了测试某种治疗方式是否对可能受多种因素影响的疾病有作用,我们应该尝试设计实验,以避免所有其他可能因素带来的影响。实现这一目标的公认方法是将志愿者随机分成两组:一组复用新药物,另一组服用安慰剂(即一种看起来像实际药物但没有生理作用的药片)。志愿者不应该知道他们是在实验组还是对照组中,实际上,如果连临床医生都不知道这些信息(即所谓的 双盲试验 (double-blind test )),那就更好了。此时,无论是志愿者还是临床医生,他们自己的偏见都无法在实验中发挥作用。由于这两组人员是从志愿者中随机选出的,我们现在可以认为:除了一组接受了新药而另一组接受了安慰剂之外,影响这两组的所有因素都是相同的。因此,这两组之间表现出的任何差异都可以归因于新药。\(\blacksquare\)
习题 8.7
340, 344, 362, 375,
356, 386, 354, 364,
332, 402, 340, 355,
362, 322, 372, 324,
318, 360, 338, 370这些数据是否与该官员的说法相矛盾?
解 8.5 .
\(H_0: \mu = 350 \quad vs \quad H_1: \mu \neq 350\)
首先计算样本数据集的样本均值和样本标准差:
\(\overline{X} = 353.75, \quad S = 21.82436\)
因此,检验统计量的值为:
\(T = \frac{\sqrt{20} (3.75)}{21.82436} = 0.7684308\)
因为这个值小于 \(|t_{0.05, 19}| = 1.730\) ,所以在 10% 的显著性水平下,接受原假设。实际上,检验数据的 \(p-\text{value}\) 为:
\(p-\text{value} = P\{ |T_{19}| > 0.7684308 \} = 2P\{ T_{19} > 0.7684308 \} = 0.4517\)
这表明在任何合理的显著性水平下,都会接受原假设,因此数据与该公共卫生官员的说法并不矛盾。 \(\blacksquare\)
可以使用 R 来计算 \(t-\text{检验}\) 。当数据位 \(x_1, ..., x_n\) 时,为了检验均值 \(\mu\) 等于 \(\mu_0\) 的原假设与均值 \(\mu\) 不等于 \(\mu_0\) 的备择假设,可以使用如下的 R 代码:
<- c (x1, ..., xn)t.test (x, mu = mu0)如上的代码会返回 \(\mu\) 的 95% 的置信区间以及原假设为真时的 \(p-\text{value}\) 。我们可以使用如下的代码来计算 习题 8.7 :
<- c (340 , 356 , 332 , 362 , 318 , 344 , 386 , 402 , 322 , 360 , 362 , 354 , 340 , 372 , 338 , 375 , 363 , 355 , 324 , 370 )t.test (x, mu = 350 )
One Sample t-test
data: x
t = 0.76843, df = 19, p-value = 0.4517
alternative hypothesis: true mean is not equal to 350
95 percent confidence interval:
343.5359 363.9641
sample estimates:
mean of x
353.75
我们可以使用 单边 \(t-\text{检验}\) 来检验假设
\(H_0: \mu = \mu_0 \quad (\text{或 } H_0: \mu \leq \mu_0) \quad vs \quad H_1: \mu > \mu_0\)
显著性水平为 \(\alpha\) 的检验是:
\[
\begin{align}
\text{接受} H_0 &, \quad \text{如果} \frac{\sqrt{n}(\overline{X} - \mu_0)}{S} \leq t_{\alpha, n-1} \\
\text{拒绝} H_0 &, \quad \text{如果} \frac{\sqrt{n}(\overline{X} - \mu_0)}{S} > t_{\alpha, n-1}
\end{align}
\tag{8.18}\]
如果 \(\frac{\sqrt{n}(\overline{X} - \mu_0)}{S} = v\) ,那么该检验的 \(p-\text{value}\) 是自由度为 \(n-1\) 的 \(t-\text{分布}\) 随机变量的值大于等于 \(v\) 的概率,即 \(1 - pt(v, n - 1)\) 。
假设: \(H_0: \mu = \mu_0 \quad (\text{或 } H_0: \mu \geq \mu_0) \quad vs \quad H_1: \mu < \mu_0\)
在显著性水平为 \(\alpha\) 下的检验是:
\[
\begin{align}
\text{接受 } H_0 &, \quad \text{ 如果 } \frac{\sqrt{n}(\overline{X} - \mu_0)}{S} \geq -t_{\alpha, n-1} \\
\text{拒绝 } H_0 &, \quad \text{ 如果 } \frac{\sqrt{n}(\overline{X} - \mu_0)}{S} < -t_{\alpha, n-1}
\end{align}
\tag{8.19}\]
该检验的 \(p-\text{value}\) 是自由度为 \(n-1\) 的 \(t-\text{分布}\) 随机变量的值小于或等于观测值 \(\frac{\sqrt{n}(\overline{X} - \mu_0)}{S}\) 的概率,即 \(pt(v, n - 1)\) 。
习题 8.8
寿命
36.1
40.2
33.8
38.5
42
35.8
37
41
36.8
37.2
33
36
在 5% 的显著性水平下,检验制造商的说法。
解 8.6 .
\(H_0: \mu \geq 40,000 \quad vs \quad H_1: \mu < 40,000\)
计算得出
\(\overline{X} = 37.2833, \quad S = 2.7319\)
因此,检验统计量的值为
\(T = \frac{\sqrt{12}(37.2833 - 40)}{2.7319} = -3.4448\)
由于 -3.4448 小于 \(t_{0.05, 11} = -1.796\) ,因此在 5% 的显著性水平下需要拒绝原假设。实际上,观察数据的 \(p-\text{value}\) 为
\(p-\text{value} = P\{ T_{11} < -3.4448 \} = P\{ T_{11} > 3.4448 \} = 0.0027\)
这表明在任何大于 0.003 的显著性水平下,我们都将拒绝制造商的说法。 \(\blacksquare\)
通过 R 提供的 单边 \(t-\text{检验}\) 函数也可以解决 习题 8.8 的问题。在 R 中,通过指定备择假设是均值小于或大于 \(\mu_0\) 来执行单边 \(t-\text{检验}\) 。也就是说,当数据为 \(x_1, ..., x_n\) 时,可以使用如下 R 代码对 \(H_0: \mu = \mu_0 \quad vs \quad H_1: \mu > \mu_0\) 进行单边 \(t-\text{检验}\) 。
<- c (x1,...,xn)t.test (x, mu = mu0, alternative = "less" )例如,对于 习题 8.8 而言,可以使用如下 R 代码:
<- c (36.1 , 40.2 , 33.8 , 38.5 , 42 , 35.8 , 37 , 41 , 36.8 , 37.2 , 33 , 36 )t.test (x, mu = 40 , alternative = "less" )
One Sample t-test
data: x
t = -3.4448, df = 11, p-value = 0.002739
alternative hypothesis: true mean is less than 40
95 percent confidence interval:
-Inf 38.69963
sample estimates:
mean of x
37.28333
习题 8.9 \(\mu\) 是服务时间的均值,\(\sigma^2\) 是服务时间的方差,那么客户在排队中花费的平均时间将由以下公式给出:
\(\frac{\lambda (\mu^2 + \sigma^2)}{2(1 - \lambda \mu)}\)
其中 \(\lambda \mu < 1\) ,并且 \(\lambda\) 是到达率。如果 \(\lambda \mu \geq 1\) ,则平均等待时间将是无限等待。因为 \(\lambda\) 是到达率,\(1/\lambda\) 是到达之间的平均时间,因此根据如上的公式可见,当 \(\mu\) 仅略小于 \(1/\lambda\) 时,平均延迟还相当大。
假设服务站的平均服务时间(每人)超过 8 分钟,那么该服务站的主管就会雇用第二名服务人员。以下数据给出了该排队系统中 28 位客户的服务时间(以分钟为单位),这些数据是否表明该服务站的平均服务时间超过 8 分钟?
8.6, 9.4, 5.0, 4.4, 3.7, 11.4, 10.0, 7.6, 14.4, 12.2, 11.0, 14.4, 9.3, 10.5, 10.3, 7.7, 8.3, 6.4, 9.2, 5.7, 7.9, 9.4, 9.0, 13.3, 11.6, 10.0, 9.5, 6.6
解 8.7 . \(p-\text{value}\) 将是平均服务时间超过 8 分钟的有力证据。利用 t.test() 对如上数据进行 \(t-\text{检测}\) 得到:检验统计量的值为 2.257,\(p-\text{value}\) 为 0.016。如此小的 \(p-\text{value}\) 无疑是平均服务时间超过 8 分钟的有力证据。
<- c (8.6 , 9.4 , 5.0 , 4.4 , 3.7 , 11.4 , 10.0 , 7.6 , 14.4 , 12.2 , 11.0 , 14.4 , 9.3 , 10.5 , 10.3 , 7.7 , 8.3 , 6.4 , 9.2 , 5.7 , 7.9 , 9.4 , 9.0 , 13.3 , 11.6 , 10.0 , 9.5 , 6.6 )t.test (x, mu = 8 , alternative = "greater" )
One Sample t-test
data: x
t = 2.2575, df = 27, p-value = 0.01613
alternative hypothesis: true mean is greater than 8
95 percent confidence interval:
8.287595 Inf
sample estimates:
mean of x
9.171429
\(\blacksquare\)
表 8.2 对本节的内容进行了总结。