Introduction
在质量控制领域,我们将 process 译作 过程 ,以强调一系列活动的内在关联性。过程指为了达到某个目标而执行的一系列操作或阶段,这种操作可以是动态的、复杂的,具有系统性和整体性,例如:生产过程、加工过程……
几乎每个工厂在生产产品的 过程 中都会存在某些 随机变异 (variation )。也就是说,无论生产 过程 控制得多么严格,生产出的产品之间总会存在一些 差异 (variation )。我们称这种 差异 (variation )为 随机变异 (chance variation ),并且我们认为这种 差异 (variation )是生产 过程 本身所固有的。
然而,在生产 过程 中,还存在另一种类型的 差异 (variation ),这种 差异 (variation )不是生产 过程 本身所固有的,而是由某些 特定原因 (assignable cause )引起的,并且通常这些 特定原因 (assignable cause )会对产品质量产生不利影响。例如,这种 差异 (variation )可能是由机器错误的设置、原材料质量较差、错误的软件、人为错误或其他更多的可能性所导致。当产品表现出的 差异 (variation )仅由 随机原因 (chance cause )而不是 特定原因 (assignable cause )导致时,我们称生产 过程 是 受控 (in control )的。
我们需要解决的一个关键问题就是:确定某个生产 过程 是 受控 (in control ) 的还是 失控 (out of control )的。
我们可以使用 控制图 (control charts )来简化确定一个 过程 是 受控 还是 失控 。控制图 由两个数字来确定:上控制限 (the upper control limits )和 下控制限 (the lower control limits )。为了使用 控制图 ,我们需要把制造 过程 生成的数据分为若干子组,并计算每个子组的统计量(例如,每个子组的平均值和标准差)。当子组的统计量超出 上下控制限 时,我们会认为 过程 是 失控 的。
在 小节 13.2 小节 13.3 过程 受控 时,产品的这些特性数据的均值和方差是固定的。我们将会介绍如何基于子组平均值(小节 13.2 小节 13.3
在 小节 13.4 属性 (attribute )将产品分类为“合格”或“不合格”,进而判断产品是否合格。然后我们将展示如何构建 控制图 (control charts )以指示产品质量的变化。
在 小节 13.5 控制图 。
最后,在 小节 13.6 控制图 ——不仅单独考虑每个子组的数据值,还会综合考虑其他子组的数据值。这类控制图包括三种不同的类型:移动平均控制图 (moving average control chart )、指数加权移动平均控制图 (exponential weighted moving average control chart )和 累积和控制图 (cumulative sum control chart )。
基于平均值构建控制图:\(\overline{x}\) 控制图
假设当 过程 处于 受控 状态时,连续生产的产品在某个可测特性上的观测数据是独立的、并且服从均值为 \(\mu\) 、方差为 \(\sigma^2\) 的正态分布。然而,由于特殊情况,该 过程 可能会失控并且生产出的产品在可观测特性上的数据开始具有不同分布。我们希望能够识别出这种失控的情况,以便停止 过程 、找出问题所在、并加以修复。
令 \(X_1, X_2, \dots\) 表示连续生产的产品的可测量特性。为了确定 过程 何时失控,我们将数据分成固定大小(记作 \(n\) )的子组。固定大小 \(n\) 的选择必须确保各子组内数据的一致性。例如,可以选择 \(n\) 以使得各子组内的所有产品都是在同一天、同一批次或同一设置下所生产的。换句话说,\(n\) 的具体值的选择,需要使得数据分布的变化更可能的发生在子组之间,而不是子组内部。\(n\) 的典型的取值为 4、5 或 6。
令 \(\overline{X}_i, i = 1,2,...\) 表示第 \(i\) 个子组的平均值,即
\[
\begin{aligned}
\overline{X}_1 &= \frac{X_1 + \cdots + X_n}{n} \\
\overline{X}_2 &= \frac{X_{n+1} + \cdots + X_{2n}}{n}\\
\overline{X}_3 &= \frac{X_{2n+1} + \cdots + X_{3n}}{n} \\
\qquad \qquad & \qquad\vdots
\end{aligned}
\]
当 过程 受控时,每个 \(X_i\) 的均值为 \(\mu\) 且方差为 \(\sigma^2\) ,因此可得:
\[
\begin{aligned}
E(\overline{X}_i) &= \mu \\
\text{Var}(\overline{X}_i) &= \frac{\sigma^2}{n}
\end{aligned}
\]
因此
\[
\frac{\overline{X}_i - \mu}{\sqrt{\sigma^2 / n}} \sim \mathcal{N}(0, 1)
\]
也就是说,过程 连续生产的产品中,如果第 \(i\) 个子组中的产品始终处于受控状态,那么随机变量 \(\sqrt{n} \frac{\overline{X}_i - \mu}{\sigma}\) 服从标准正态分布。因此,标准正态随机变量 \(Z\) 几乎总是位于 \(-3\) 和 \(+3\) 之间。(实际上,\(P\{-3 < Z < 3\} = 0.9973\) 。)因此,如果 过程 在连续生产的产品中,第 \(i\) 个子组的产品始终处于受控状态,那么我们一定可以期望得到:
\[
-3 < \sqrt{n} \frac{\overline{X}_i - \mu}{\sigma} < 3
\]
即,
\[
\mu - \frac{3\sigma}{\sqrt{n}} < \overline{X}_i < \mu + \frac{3\sigma}{\sqrt{n}}
\]
我们称
\[
\begin{aligned}
\text{UCL} &\equiv \mu + \frac{3\sigma}{\sqrt{n}} \\
\text{LCL} &\equiv \mu - \frac{3\sigma}{\sqrt{n}}
\end{aligned}
\]
分别为 上控制限 (upper control limits )和 下控制限 (lower control limit )。
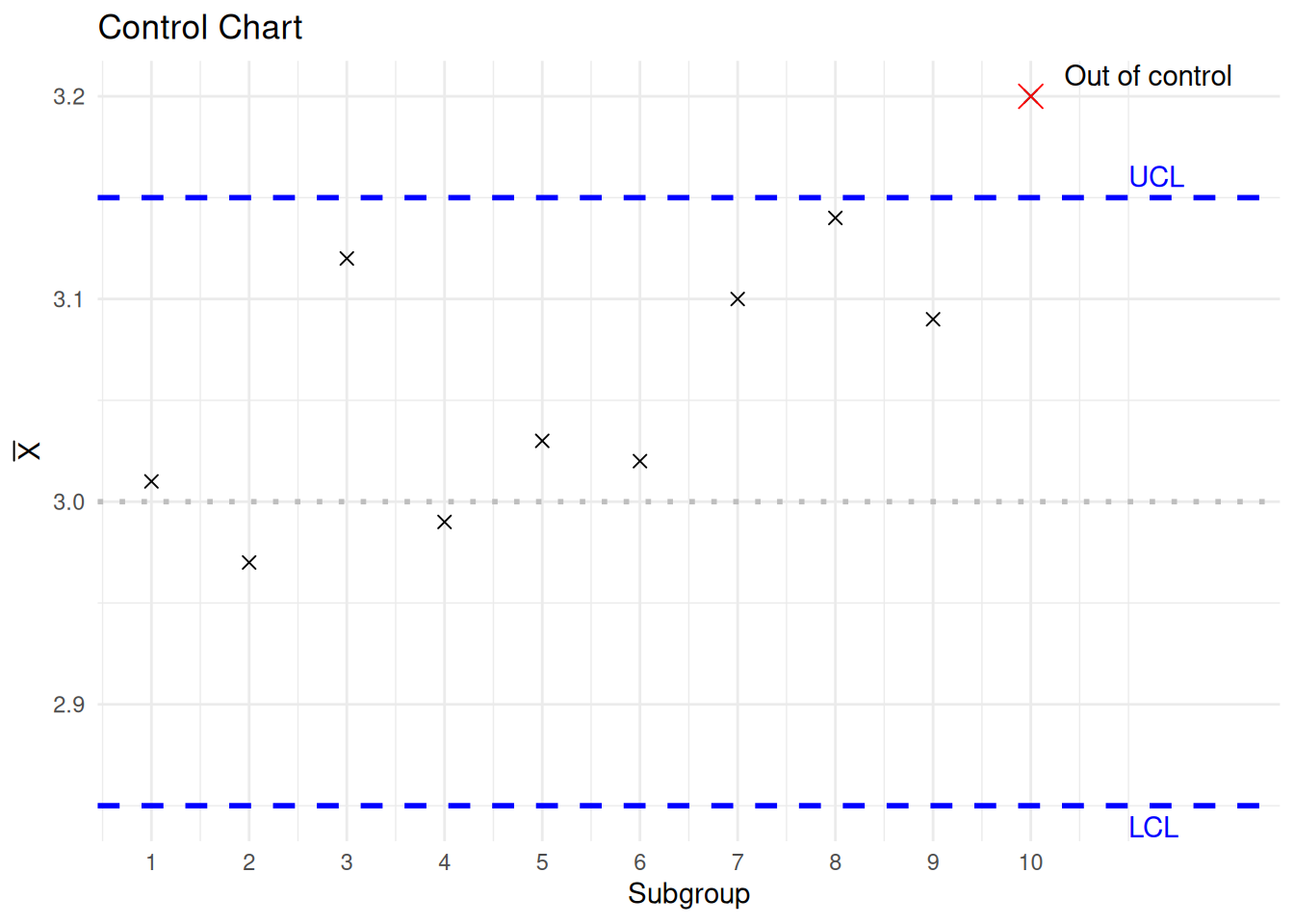
\(\overline{X}\) 控制图的作用是检测产品的平均值是否发生变化,其方法是绘制连续子组的平均值 \(\overline{X}_i\) ,并在 \(\overline{X}_i\) 第一次落在 \(\text{LCL}\) 和 \(\text{UCL}\) 之外时,判断 过程 已经失控(见 图 13.1 )。
习题 13.1
1
3.01
2
2.97
3
3.12
4
2.99
5
3.03
6
3.02
7
3.10
8
3.14
9
3.09
10
3.20
根据如上的数据,我们应得出什么结论?
解 13.1 . 过程 处于受控状态时,连续生产的钢轴直径服从均值 \(\mu = 3\) 、标准差 \(\sigma = 0.1\) 的正态分布。因此,当 \(n = 4\) 时:
\[
\begin{aligned}
\text{LCL} &= 3 - \frac{3(0.1)}{\sqrt{4}} = 2.85 \\
\text{UCL} &= 3 + \frac{3(0.1)}{\sqrt{4}} = 3.15
\end{aligned}
\]
由于第 10 子组的样本平均值大于 上控制限 (UCL ),因此可以怀疑钢轴的平均直径已经不再是 3mm。(显然,从第 6 到第 10 子组样本的结果来看,其平均直径看起来已经超过了 3mm。)
代码
library (ggplot2)<- c (3.01 , 2.97 , 3.12 , 2.99 , 3.03 , 3.02 , 3.10 , 3.14 , 3.09 , 3.20 )<- seq_along (x)<- data.frame (i= i, x= x)<- 3 # 均值 <- 0.1 # 标准差 <- 4 # 子组样本量 <- mu + 3 * sigma / sqrt (n) # 上控制限 <- mu - 3 * sigma / sqrt (n) # 下控制限 ggplot (df, aes (x = i, y = x)) + geom_point (shape = 4 , size = 2 ) + # 绘制均值点 #geom_line(aes(group = 1), color = "black") + # 连接均值点的线 geom_hline (yintercept = UCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 上控制限 geom_hline (yintercept = LCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 下控制限 geom_hline (yintercept = mu, color = "gray" , linetype = "dotted" , size = 1 ) + # 中心线 annotate ("text" , x = 11 , y = UCL, label = "UCL" , hjust = 0 , vjust = - 0.5 , color = "blue" ) + # 标注UCL annotate ("text" , x = 11 , y = LCL, label = "LCL" , hjust = 0 , vjust = 1.5 , color = "blue" ) + # 标注LCL annotate ("text" , x = 10 , y = x[10 ], label = "Out of control" , hjust = - 0.2 , vjust = - 0.5 , color = "black" ) + # 标注失控点 geom_point (data= df[10 , ], aes (x = i, y = x), color = "red" , shape = 4 , size = 4 ) + # 突出显示失控点 labs (title = "Control Chart" , x = "Subgroup" , y = expression (bar (X))) + # 添加标题和轴标签 scale_x_continuous (limits = c (1 , 12 ),breaks = seq (1 , 10 , by = 1 )) + theme_minimal () # 使用简洁主题
需要注意的是,即使 过程 处于受控状态,子组均值也有概率位于控制界限之外,以 习题 13.1 的数据为例,位于控制界限之外的概率是 0.0027。因此,我们可能会错误地停止 过程 并去寻找那些本来就不存在的问题源。
假设 过程 刚刚失控,并且测量数据的均值从 \(\mu\) 变为 \(\mu + a\) ,其中 \(a > 0\) 。如果之后没有进一步变化,那么需要多长时间才能从控制图上观察到 过程 已经失控?为了回答这个问题,子组均值落在控制界限内的条件是:
\(-3 < \sqrt{n} \frac{\overline{X} - \mu}{\sigma} < 3\)
即,
\(-3 - \frac{a \sqrt{n}}{\sigma} < \sqrt{n} \frac{\overline{X} - \mu}{\sigma} - \frac{a\sqrt{n}}{\sigma} < 3 - \frac{a \sqrt{n}}{\sigma}\)
所以,
\(-3 - \frac{a \sqrt{n}}{\sigma} < \sqrt{n} \frac{\overline{X} - \mu - a}{\sigma} < 3 - \frac{a \sqrt{n}}{\sigma}\)
因此,子组均值 \(\overline{X}\) 服从均值为 \(\mu + a\) 、方差为 \(\sigma^2 / n\) 的正态分布。因此,
\(\sqrt{n}\frac{\overline{X} - \mu - a}{\sigma}\) 服从标准正态分布,其落在控制界限内的概率为:
\[
\begin{aligned}
P \left\{ -3 - \frac{a \sqrt{n}}{\sigma} < Z < 3 - \frac{a \sqrt{n}}{\sigma} \right\} &= \Phi \left( 3 - \frac{a \sqrt{n}}{\sigma} \right) - \Phi \left( -3 - \frac{a \sqrt{n}}{\sigma} \right) \\
&\approx \Phi \left( 3 - \frac{a \sqrt{n}}{\sigma} \right)
\end{aligned}
\]
因此,落在控制界限外的概率约为:
\(1 - \Phi \left( 3 - \frac{a \sqrt{n}}{\sigma} \right)\)
例如,如果子组大小 \(n = 4\) ,均值增加 \(1\) 个标准差,即 \(a = \sigma\) ,那么子组均值落在控制界限之外的概率为:
\(1 - \Phi(1) \approx 0.1587\)
由于每个子组均值落在控制界限之外都是相互独立的,切其概率为 \(1 - \Phi \left( 3 - \frac{a \sqrt{n}}{\sigma} \right)\) ,因此检测到此变化所需的子组数量服从几何分布,其均值为:
\(\left[ 1 - \Phi \left( 3 - \frac{a \sqrt{n}}{\sigma} \right) \right]^{-1}\)
在 \(n = 4\) 的情况下,如果均值变化为 1 个标准差,为检测均值发生 1 个标准差变化,需要绘制的子组数量服从几何分布,其均值为:
\(\frac{1}{0.1587} \approx 6.301\) 。
\(\mu\) 、\(\sigma\) 未知的场景
如果我们刚开始使用控制图,并且没有可靠的历史数据,那么 \(\mu\) 和 \(\sigma\) 则都是未知的。此时,我们需要估计 \(\mu\) 和 \(\sigma\) 。为此,我们使用 \(k\) 个子组,其中 \(k\) 应满足 \(k \geq 20\) 且 \(nk \geq 100\) 。如果 \(\overline{X}_i,\ i = 1, \ldots, k\) 是第 \(i\) 个子组的平均值,那么可以通过这些子组平均值的均值 \(\overline{\overline{X}}\) 来估计 \(\mu\) ,即:
\[
\overline{\overline{X}} = \frac{\overline{X}_1 + \cdots + \overline{X}_k}{k}
\]
为了估计 \(\sigma\) ,令 \(S_i\) 表示第 \(i\) 个子组的样本标准差,其中 \(i = 1, \ldots, k\) 。即:
\[
\begin{aligned}
S_1 &= \sqrt{\frac{\sum_{i=1}^n (X_i - \overline{X}_1)^2}{n-1}} \\
S_2 &= \sqrt{\frac{\sum_{i=1}^n (X_{n+i} - \overline{X}_2)^2}{n-1}} \\
\quad & \quad \vdots \\
S_k &= \sqrt{\frac{\sum_{i=1}^n (X_{(k-1)n+i} - \overline{X}_k)^2}{n-1}}
\end{aligned}
\]
令:
\[
\overline{S} = \frac{S_1 + \cdots + S_k}{k}
\]
统计量 \(\overline{S}\) 并不是 \(\sigma\) 的无偏估计,即 \(E[\overline{S}] \neq \sigma\) 。为了将 \(\overline{S}\) 转化为无偏估计,我们首先计算 \(E[\overline{S}]\) :
\[
E[\overline{S}] = \frac{E[S_1] + \cdots + E[S_k]}{k} = E[S_1]
\tag{13.1}\]
最后一个等式成立是因为 \(S_1, \ldots, S_k\) 是独立且同分布的(因此具有相同的均值)。为了计算 \(E[S_1]\) ,我们需要用到 定理 6.2 中的正态分布样本的基本概念,即:
\[
(n-1)\frac{S_1^2}{\sigma^2} = \sum_{i=1}^n \frac{(X_i - \overline{X}_1)^2}{\sigma^2} \sim \chi^2_{n-1}
\tag{13.2}\]
现在可以证明(参见习题 3):
\[
E[\sqrt{Y}] = \frac{\sqrt{2}\Gamma(n/2)}{\Gamma(\frac{n-1}{2})}, \quad \text{当} \, Y \sim \chi^2_{n-1}
\tag{13.3}\]
由于
\[
E\left[\sqrt{(n-1)S^2/\sigma^2}\right] = \sqrt{n-1}E[S_1]/\sigma
\]
根据 式 13.2 和 式 13.3 ,我们可以得出:
\[
E[S_1] = \frac{\sqrt{2}\Gamma(n/2)\sigma}{\sqrt{n-1}\Gamma(\frac{n-1}{2})}
\]
因此,如果定义
\[
c(n) = \frac{\sqrt{2}\Gamma(n/2)}{\sqrt{n-1}\Gamma(\frac{n-1}{2})}
\]
则根据 式 13.1 ,可以推导出 \(\overline{S}/c(n)\) 是 \(\sigma\) 的无偏估计量。
表 13.1 展示了从 \(n=2\) 到 \(n=10\) 的 \(c(n)\) 的值。
在计算 表 13.1 中的数值时,\(\Gamma(n/2)\) 和 \(\Gamma\left(n - \frac{1}{2}\right)\) 的计算基于我们在 ?sec-5_7 中已经构建的递归公式:
\[
\Gamma(a) = (a - 1)\Gamma(a - 1)
\]
递归公式表明,对于整数 \(n\) ,有:
\[
\begin{aligned}
\Gamma(n) &= (n - 1)(n - 2) \cdots 3 \cdot 2 \cdot 1 \cdot \Gamma(1) \\
&= (n - 1)! \quad \because \quad \Gamma(1) = \int_{0}^{\infty} e^{-x} \, dx = 1
\end{aligned}
\]
类似的,我们可得到如下的递归公式:
\[
\Gamma\left(\frac{n + 1}{2}\right) = \left(\frac{n - 1}{2}\right)\left(\frac{n - 3}{2}\right)\cdots\frac{3}{2} \cdot \frac{1}{2} \cdot \Gamma\left(\frac{1}{2}\right)
\]
\[
\begin{aligned}
\Gamma\left(\frac{1}{2}\right) &= \int_{0}^{\infty} e^{-x} x^{-1/2} \, dx \\
&= \int_{0}^{\infty} e^{-y^2/2} \frac{\sqrt{2}}{y} \, y \, dy \quad \text{by } x = \frac{y^2}{2}, \, dx = y \, dy \\
&= \sqrt{2} \int_{0}^{\infty} e^{-y^2/2} \, dy \\
&= 2\sqrt{\pi} \cdot \frac{1}{\sqrt{2\pi}} \int_{0}^{\infty} e^{-y^2/2} \, dy \\
&= 2\sqrt{\pi} \cdot P[N(0, 1) > 0] \\
&= \sqrt{\pi}
\end{aligned}
\]
本节所述的对 \(\mu\) 和 \(\sigma\) 的估计用到了所有的 \(k\) 个子组,因此,只有当整个 过程 都处于受控状态时才是合理的。为了检验这一点,我们基于 \(\mu\) 和 \(\sigma\) 的估计值来计算 控制限 (the control limits ),即:
\[
\begin{aligned}
\text{LCL} & = \overline{\overline{X}}-\frac{3\overline{S}}{c(n)\sqrt{n}} \\
\text{UCL} & = \overline{\overline{X}}+\frac{3\overline{S}}{c(n)\sqrt{n}}
\end{aligned}
\tag{13.4}\]
接下来,我们检查每个子组的平均值 \(\overline{X}_i\) 是否落在上下控制限之间。我们删除那些平均值未落在控制限内的子组(假设 过程 暂时失控),然后重新计算 \(\mu\) 和 \(\sigma\) 的估计值。然后,我们再次检查所有剩余子组的平均值是否都位于控制限之间。如果还存在子组的的平均值未落在控制限内,删除这些子组,如此反复。当然,如果有过多的子组平均值落在控制限之外,就表明 过程 尚未处于受控状态。
习题 13.2 习题 13.1 而言,假设该 过程 刚刚开始,因此均值 \(\mu\) 和标准差 \(\sigma\) 是未知的。在这种场景下,我们重新来考虑下 习题 13.1 。此时,假设样本标准差如下所示:
1
3.01
0.12
6
3.02
0.08
2
2.97
0.14
7
3.10
0.15
3
3.12
0.08
8
3.14
0.16
4
2.99
0.11
9
3.09
0.13
5
3.03
0.09
10
3.20
0.16
因为 \(\overline{\overline{X}} = 3.067\) ,\(\overline{S} = 0.122\) ,\(c(4) = 0.9213\) ,控制限为:
\(\text{LCL} = 3.067 - \frac{3 \times 0.122}{2 \times 0.9213} = 2.868\) \(\text{UCL} = 3.067 + \frac{3 \times 0.122}{2 \times 0.9213} = 3.266\)
由于所有的 \(\overline{X}_i\) 均落在控制限内,因此我们假设该 过程 处于控制状态,且均值为 \(\mu = 3.067\) ,标准差为:\(\sigma = \frac{\overline{S}}{c(4)} = 0.1324\) 。
假设该生产线生产的产品的规格应该为 \(3 \pm 0.1\) 。假设该 过程 保持处于受控状态,且上述数据是对真实均值和标准差的准确估计,计算满足规格的产品的比例?
解 13.2 . \(\mu = 3.067\) ,\(\sigma = 0.1324\) 下,我们有:
\[
\begin{align}
P\{2.9 \leq X \leq 3.1\} &= P\left\{ \frac{2.9 - 3.067}{0.1324} \leq \frac{X - 3.067}{0.1324} \leq \frac{3.1 - 3.067}{0.1324} \right\} \\
&= \Phi(0.2492) - \Phi(-1.2613) \\
&= 0.5984 - 0.1036 \\
&= 0.4948
\end{align}
\]
因此,满足规格要求的产品比例为 49%。\(\blacksquare\)
1.
估计量 \(\overline{\overline{X}}\) 等于所有 \(nk\) 个测量值的平均值,因此,显然,\(\overline{\overline{X}}\) 是 \(\mu\) 的估计量。然而,为什么不直接使用所有 \(nk\) 个测量值的样本标准差(如下式所示)作为 \(\sigma\) 的初始估计量可能并不直观:
\(S \equiv \sqrt{\frac{\sum_{i=1}^{nk} \left( X_i - \overline{\overline{X}} \right)^2}{nk - 1}}\)
主要的原因在于:过程 在前 \(k\) 个子组期间可能并非始终处于受控状态,因此如上式所示的估计量可能与真实值之间相差甚远。此外,一个 过程 可能会由于某些突发事件而失控,从而导致均值 \(\mu\) 发生变化,而标准差却保持不变。在这种情况下,各子组的样本标准差仍然可以作为 \(\sigma\) 的估计量,而 \(S\) 却不能。
即使整个 过程 看似均处于受控状态,\(\sigma\) 的无偏估计量 \(\frac{\overline{S}}{c(n)}\) 仍然要优于样本标准差 \(S\) 。这是因为:我们不能确定在此期间均值终没有发生变化。例如,即使所有子组均值都落在控制限内,我们判断该 过程 处于受控状态,但这并不能保证不存在某些特定原因导致的差异(这些特定原因导致的差异可能导致均值发生变化,但这些变化尚未在图表中体现出来)。这意味着在实际操作中,即使假设 过程 处于受控状态并持续生产产品,我们也需要认识到可能会存在某些特定原因导致的差异。由此认为,\(\frac{\overline{S}}{c(n)}\) 是一个比样本标准差更“安全”的估计量。换句话说,当 过程 始终受控时,\(\frac{\overline{S}}{c(n)}\) 的表现可能不如样本标准差好;但如果均值存在些微小变化,\(\frac{\overline{S}}{c(n)}\) 的表现会比样本标准差要好很多。
2.
以前,我们常使用基于子组极差(subgroup ranges )——即子组中最大值与最小值之差来作为 \(\sigma\) 的估计量。这种方法的目的主要是简化必要的计算量(显然,计算极差比计算子组的样本标准差要容易得多)。然而,随着现代计算机能力的增强,计算量已经不再是一个需要考虑的限制因素。此外,标准差估计量的方差比极差估计量的方差更小,并且鲁棒性也更好(即使背后的数据分布不是正态分布,标准差估计量仍能提供合理的总体标准差估计)。因此,在本书中,我们不考虑极差估计量。
\(\text{S}\) -控制图
小节 13.2 \(\overline{X}\) 的控制图主要用于检测总体均值的变化。但有时候,我们也需要关注总体方差可能发生变化的情况下,此时可以使用 \(\text{S}\) -控制图。
假设 过程 在受控状态下所生产的产品具有可测量的特性,这些特性服从均值为 \(\mu\) 、方差为 \(\sigma^2\) 的正态分布。若 \(S_i\) 是第 \(i\) 个子组的样本标准差,则:
\(S_i = \sqrt{\frac{\sum_{j=1}^n \left( X_{(i-1)n+j} - \overline{X}_i \right)^2}{n-1}}\)
如 小节 13.2.1
\[
E[S_i] = c(n)\sigma
\tag{13.5}\]
此外,\(S_i\) 的方差为:
\[
\begin{align}
\text{Var}(S_i) &= E[S_i^2] - \left(E[S_i]\right)^2 \\
&= \sigma^2 - c^2(n)\sigma^2 \\
&= \sigma^2[1 - c^2(n)]
\end{align}
\tag{13.6}\]
当 过程 处于受控状态时,\(S_i\) 服从一个常数(\(\sigma / \sqrt{n-1}\) )乘以一个自由度为 \(n-1\) 的卡方随机变量的平方根(\(\sqrt{\chi^2_{n-1}}\) )的分布(\(\frac{\sigma}{\sqrt{n-1}}\sqrt{\chi^2_{n-1}}\) )。
可以证明,\(S_i\) 落在其均值 3 个标准差范围内的概率接近于 1,即:
\(P\{E[S_i] - 3\sqrt{\text{Var}(S_i)} < S_i < E[S_i] + 3\sqrt{\text{Var}(S_i)}\} \approx 0.99\)
因此,利用 式 13.5 和 式 13.6 中的 \(E[S_i]\) 和 \(\text{Var}(S_i)\) ,\(\text{S}\) -控制图的上、下控制限可以设置为:
\[
\begin{align}
\text{UCL} &= \sigma \left[c(n) + 3\sqrt{1 - c^2(n)}\right] \\
\text{LCL} &= \sigma \left[c(n) - 3\sqrt{1 - c^2(n)}\right]
\end{align}
\tag{13.7}\]
在图中连续绘制 \(S_i\) ,以确认 \(S_i\) 是否落在上、下控制限之内。当某个 \(S_i\) 落在控制限之外时,应该停止 过程 ,并认为该 过程 已经处于失控状态。
当我们从起始阶段开始绘制控制图时,\(\sigma\) 还是未知的,此时可以使用 \(\overline{S}/c(n)\) 来估计 \(\sigma\) 。基于 式 13.7 ,估计的控制限为:
\[
\begin{align}
\text{UCL} &= \overline{S} \left[1 + 3\sqrt{\frac{1 - c^2(n)}{c^2(n)}}\right] \\
\text{LCL} &= \overline{S} \left[1 - 3\sqrt{\frac{1 - c^2(n)}{c^2(n)}}\right]
\end{align}
\tag{13.8}\]
就像在刚开始绘制 \(\overline{X}\) 控制图时那样,在绘制 \(\text{S}\) -控制图时,也应检查 \(k\) 个子组的样本标准差 \(S_1, S_2, \dots, S_k\) 是否都落在控制限内。如果任何一个子组的 \(S_i\) 落在控制限之外,则应舍弃这些子组并重新计算 \(\overline{S}\) 。
例 13.1 过程 的 20 个子组(每组大小为 5)的 \(\overline{X}\) 和 \(S\) 值 如下表所示。
1
35.1
4.2
6
36.4
4.5
11
38.1
4.2
16
41.3
8.2
2
33.2
4.4
7
35.9
3.4
12
37.6
3.9
17
35.7
8.1
3
31.7
2.5
8
38.4
5.1
13
38.8
3.2
18
36.3
4.2
4
35.4
3.2
9
35.7
3.8
14
34.3
4.0
19
35.4
4.1
5
34.5
2.6
10
27.2
6.2
15
43.2
3.5
20
34.6
3.7
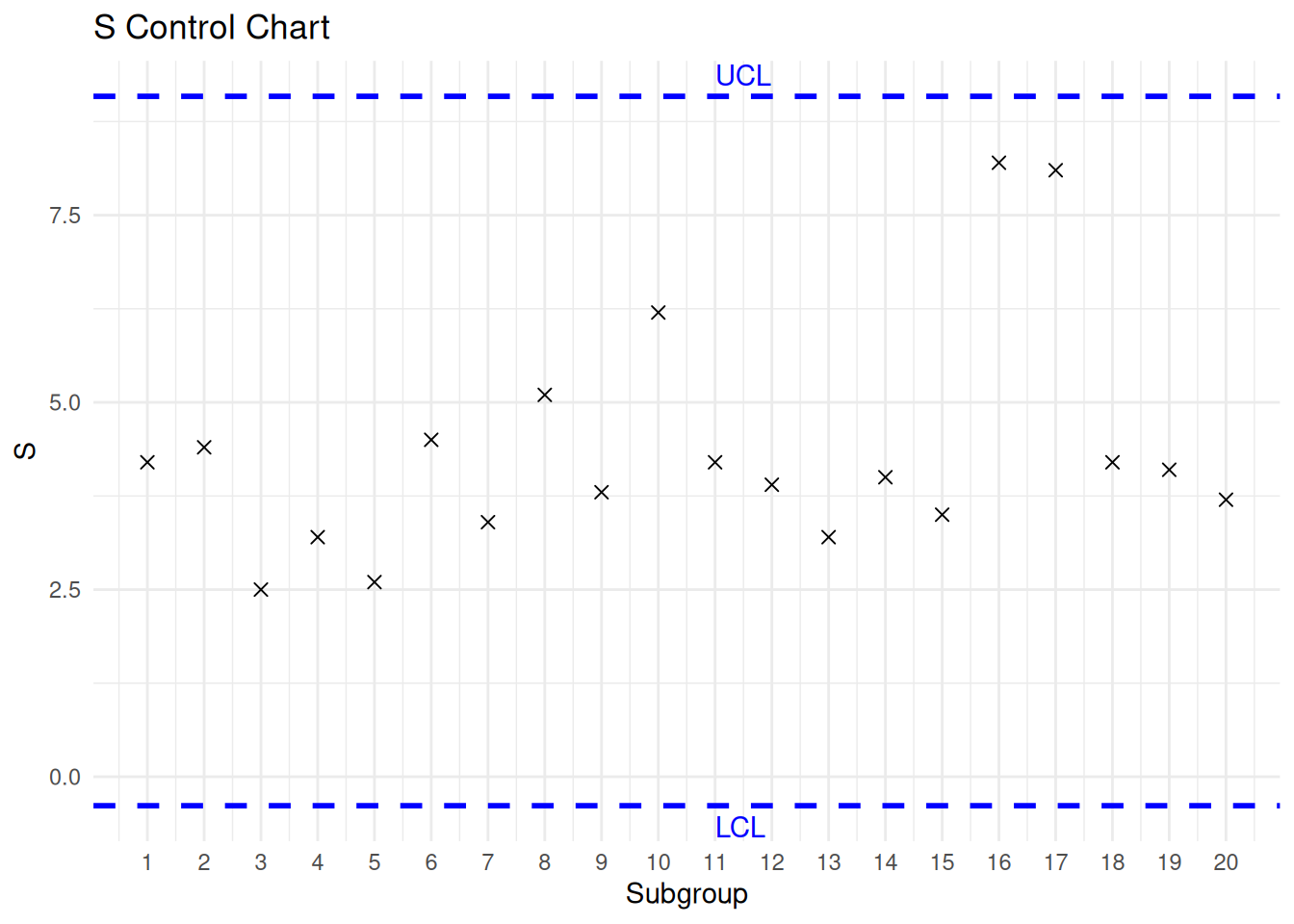
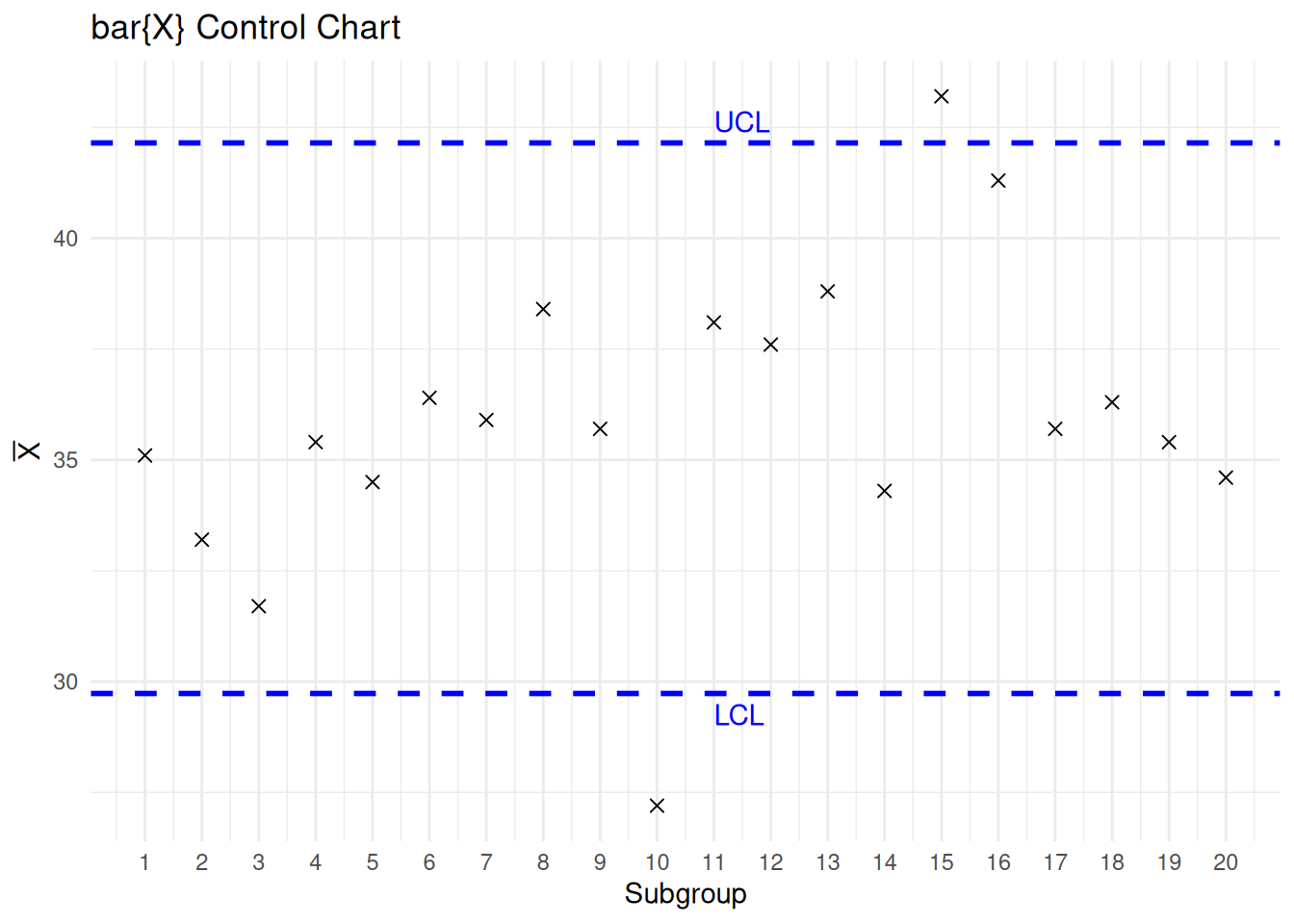
由于 \(\overline{\overline{X}} = 35.94\) ,\(\overline{S} = 4.35\) ,\(c(5) = 0.9400\) ,根据 式 13.4 和 式 13.8 可以得出 \(\overline{X}\) 和 \(S\) 的初始上下控制限为:
\(\text{UCL}(\overline{X}) = 42.149\) \(\text{LCL}(\overline{X}) = 29.731\) \(\text{UCL}(S) = 9.087\) \(\text{LCL}(S) = -0.386\)
根据上述控制限绘制的 \(S\) 控制图和 \(\overline{X}\) 控制图分别如 图 13.2 (a) 和 图 13.2 (b)。由于 \(\overline{X}_{10}\) 和 \(\overline{X}_{15}\) 超出了 \(\overline{X}\) 的控制限,必须剔除这些子组,并重新计算控制限(我们将必要的计算留作练习)。
代码
library (ggplot2)# S control chart. <- c (4.2 , 4.4 , 2.5 , 3.2 , 2.6 , 4.5 , 3.4 , 5.1 , 3.8 , 6.2 , 4.2 , 3.9 , 3.2 , 4.0 , 3.5 , 8.2 , 8.1 , 4.2 , 4.1 , 3.7 )<- seq_along (x)<- data.frame (i= i, x= x)<- 9.087 # 上控制限 <- - 0.386 # 下控制限 ggplot (df, aes (x = i, y = x)) + geom_point (shape = 4 , size = 2 ) + # 绘制均值点 geom_hline (yintercept = UCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 上控制限 geom_hline (yintercept = LCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 下控制限 annotate ("text" , x = 11 , y = UCL, label = "UCL" , hjust = 0 , vjust = - 0.5 , color = "blue" ) + # 标注UCL annotate ("text" , x = 11 , y = LCL, label = "LCL" , hjust = 0 , vjust = 1.5 , color = "blue" ) + # 标注LCL labs (title = "S Control Chart" , x = "Subgroup" , y = expression (S)) + # 添加标题和轴标签 scale_x_continuous (limits = c (1 , 20 ),breaks = seq (1 , 20 , by = 1 )) + theme_minimal () # 使用简洁主题 # \overline{X} control chart. <- c (35.1 , 33.2 , 31.7 , 35.4 , 34.5 , 36.4 , 35.9 , 38.4 , 35.7 , 27.2 , 38.1 , 37.6 , 38.8 , 34.3 , 43.2 , 41.3 , 35.7 , 36.3 , 35.4 , 34.6 )<- seq_along (x)<- data.frame (i= i, x= x)<- 42.149 # 上控制限 <- 29.731 # 下控制限 ggplot (df, aes (x = i, y = x)) + geom_point (shape = 4 , size = 2 ) + # 绘制均值点 geom_hline (yintercept = UCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 上控制限 geom_hline (yintercept = LCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 下控制限 annotate ("text" , x = 11 , y = UCL, label = "UCL" , hjust = 0 , vjust = - 0.5 , color = "blue" ) + # 标注UCL annotate ("text" , x = 11 , y = LCL, label = "LCL" , hjust = 0 , vjust = 1.5 , color = "blue" ) + # 标注LCL labs (title = "bar{X} Control Chart" , x = "Subgroup" , y = expression (bar (X))) + # 添加标题和轴标签 scale_x_continuous (limits = c (1 , 20 ),breaks = seq (1 , 20 , by = 1 )) + theme_minimal () # 使用简洁主题
\(\blacksquare\)
不合格品率控制图
当测量的数据值是在某个范围内连续变化时,可以使用 \(\overline{X}\) -控制图和 \(S\) -控制图判断 过程 是否处于受控状态。但有时候,可直接将所生产的产品分类为有缺陷或无缺陷,此时,我们依然可以构建控制图。
假设当 过程 处于受控状态时,所生产的每个产品出现缺陷的概率相互独立且为 \(p\) 。令 \(X\) 表示大小为 \(n\) 的产品子组中缺陷产品的数量,那么在 过程 受控的假设下,\(X\) 将是一个参数为 \((n, p)\) 的二项随机分布。如果 \(F = X / n\) 是子组缺陷产品的比例,那么在 过程 受控的假设下,其均值和标准差由以下公式给出:
\(E[F]=\frac{E[X]}{n}=\frac{np}{n}=p\)
\(\sqrt{\text{Var}(F)}=\sqrt{\frac{\text{Var}(X)}{n^2}}=\sqrt{\frac{np(1 - p)}{n^2}}=\sqrt{\frac{p(1 - p)}{n}}\)
因此,当 过程 处于受控状态时,大小为 \(n\) 的子组中缺陷产品的比例很可能在以下范围内:
\(\text{LCL}=p - 3\sqrt{\frac{p(1 - p)}{n}}, \quad \text{UCL}=p + 3\sqrt{\frac{p(1 - p)}{n}}\)
对于本节的场景,子组大小 \(n\) 通常比 \(\overline{X}\) -控制图和 \(S\) -控制图中使用的 4~10 的典型值要大得多。选择更大的 \(n\) 的主要原因在于:如果 \(p\) 很小且 \(n\) 的大小不合理,那么即使 过程 失控,大多数子组也将没有缺陷产品。因此,与 \(np\) 不接近于零的 \(n\) 相比,\(np\) 接近于零的 \(n\) 在检测质量变化时需要花费更长的时间。
当然,要启动这样一个控制图,我们首先必须要估计 \(p\) 。为此,选择 \(k\) 个子组,并尽量使 \(k\geq20\) ,同时令 \(F_i\) 表示第 \(i\) 个子组中缺陷产品的比例。\(p\) 的估计值由 \(\overline{F}\) 给出,其定义为:
\(\overline{F}=\frac{F_1+\cdots + F_k}{k}\)
由于 \(nF_i\) 等于第 \(i\) 个子组中的缺陷产品数量,则 \(\overline{F}\) 也可以表示为:
\[
\begin{align*}
\overline{F}&=\frac{nF_1+\cdots + nF_k}{nk}\\
&=\frac{\text{所有子组中的缺陷产品总数}}{\text{所有子组中的产品总数}}
\end{align*}
\]
换句话说,\(p\) 的估计值就是所检查产品中缺陷产品的比例。此时上控制限和下控制限由以下公式给出:
\(\text{LCL}=\overline{F}-3\sqrt{\frac{\overline{F}(1 - \overline{F})}{n}}, \quad \text{UCL}=\overline{F}+3\sqrt{\frac{\overline{F}(1 - \overline{F})}{n}}\)
现在,我们就可以检查子组的缺陷比例 \(F_1,F_2,\cdots,F_k\) 是否落在如上的控制限内。如果某些子组超出了控制限范围,那么应该剔除相应的子组,并重新计算 \(\overline{F}\) 。
例 13.2
1
6
.12
11
1
.02
2
5
.10
12
3
.06
3
3
.06
13
2
.04
4
0
.00
14
0
.00
5
1
.02
15
1
.02
6
2
.04
16
1
.02
7
1
.02
17
0
.00
8
0
.00
18
2
.04
9
2
.04
19
1
.02
10
1
.02
20
2
.04
\(\overline{F} = \frac{缺陷产品总数}{产品总数} = \frac{34}{1000} = 0.034\)
因此,
\[
\begin{align*}
\text{UCL}&= 0.034 + 3\sqrt{\frac{(0.034)(0.968)}{50}}= 0.1109\\
\text{LCL}&= 0.034 - 3\sqrt{\frac{(0.034)(0.966)}{50}}=- 0.0429
\end{align*}
\]
由于第一个子组中的缺陷产品比例超出了上控制限,我们需要剔除该子组并重新计算 \(\overline{F}\) :
\(\overline{F}=\frac{34 - 6}{950}=0.0295\)
因此,新的上控制限和下控制限为 \(0.0295\pm\sqrt{(0.0295)(1 - 0.0295)/50}\) ,即
\(\text{LCL}=-0.0423, \quad \text{UCL}=0.1013\)
由于其余子组的缺陷品比例都落在控制限内,我们可以接受这样的结论:当 过程 受控时,子组中的缺陷品比例应低于 \(0.1013\) 。\(\blacksquare\)
请注意,即使质量变化可能会意味着质量提升,我们也试图检测到任何质量上的变化。也就是说,即使次品出现的概率降低,我们也将该过程视为“失控”。这样做的原因是,注意到质量上的任何变化(无论是变好还是变差)都很重要,以便能够评估变化的原因。换句话说,如果产品质量出现了提升,那么分析生产过程以确定质量提升的原因就很重要。(也就是说,我们做对了哪些事情?)
缺陷数控制图
在本节中,我们将考虑由一个或一组产品构成的产品单元中的缺陷产品数量的场景,例如:飞机机翼中有缺陷的铆钉数量,某芯片公司每天生产的有缺陷的计算机芯片数量。本节分析的场景中,通常待检测的产品的数量比较大,并且实际出现缺陷的概率都很小,所以假设由此产生的缺陷数量服从泊松分布是合理的。因此,我们假设,当 过程 处于受控状态时,单位缺陷数量(number of defects per unit )服从均值为 \(\lambda\) 的泊松分布。
如果我们令 \(X_i\) 表示第 \(i\) 个单元中的缺陷数量,那么,由于泊松随机变量的方差等于其均值,当 过程 处于受控状态时:
\(E[X_i]=\lambda, \quad \text{Var}(X_i)=\lambda\)
因此,当 过程 处于受控状态时,\(X_i\) 很可能在 \(\lambda\pm3\sqrt{\lambda}\) 范围内,所以上控制限和下控制限由以下公式给出:
\(\text{UCL}=\lambda + 3\sqrt{\lambda}, \quad \text{LCL}=\lambda - 3\sqrt{\lambda}\)
如前所述,当一开始绘制控制图、且 \(\lambda\) 未知时,应该使用 \(k\) 个单元的样本来估计 \(\lambda\) :
\(\overline{X}=(X_1+\cdots + X_k)/k\)
由此我们得到控制限:
\(\overline{X}+3\sqrt{\overline{X}} \quad, \quad \overline{X}-3\sqrt{\overline{X}}\)
如果所有的 \(X_i\) (\(i = 1,\cdots,k\) )都落在控制限内,那么我们就假设 过程 处于受控状态,且 \(\lambda = \overline{X}\) 。如果存在 \(X_i\) 超出控制限,那么就剔除这些数据并重新计算 \(\overline{X}\) ,依此类推。
在每个产品(或每天)的平均缺陷数较小的情况下,应该将产品(天数)组合起来,并使用给定数量——比如 \(n\) 个产品(或 \(n\) 天)——的缺陷数作为样本数据。由于独立泊松随机变量的和仍然是均值为 \(\lambda\) 的泊松随机变量,因此给定数量的缺陷数据将是一个均值更大的 \(\lambda\) 的泊松随机变量。所以,当每个产品的平均缺陷数小于 25 时,这种产品组合的方式是有用的。
为了体会产品组合的优势,假设当 过程 处于受控状态时,每个产品的平均缺陷数为 4,并且假设发生了一些情况,导致这个值从 4 变为 6,也就是说,产品缺陷数增加了 1 个标准差。那么,当连续数据由 \(n\) 个产品中的缺陷数组成时,平均要生产多少个产品才能判断 过程 为失控状态。
由于在受控状态下,\(n\) 个产品样本中的缺陷数服从均值和方差都等于 \(4n\) 的泊松分布,所以控制限为 \(4n\pm3\sqrt{4n}\) ,即 \(4n\pm6\sqrt{n}\) 。现在,如果每个产品的平均缺陷数变为 6,那么将服从均值为 \(6n\) 的泊松分布,所以此时样本落在控制限之外的概率(称其为 \(p(n)\) )由下式给出:
\(p(n)=P\{Y > 4n + 6\sqrt{n}\}+P\{Y < 4n - 6\sqrt{n}\}\)
其中 \(Y\) 服从均值为 \(6n\) 的泊松分布。现在
\[
\begin{align*}
p(n) &\approx P\{Y > 4n + 6\sqrt{n}\} \\
&=P\left\{\frac{Y - 6n}{\sqrt{6n}}>\frac{6\sqrt{n}-2n}{\sqrt{6n}}\right\}\\
&\approx P\left\{Z>\frac{6\sqrt{n}-2n}{\sqrt{6n}}\right\}\quad \text{其中 }Z\sim \mathcal{N}(0,1)\\
&=1 - \Phi\left(\sqrt{6}-2\sqrt{\frac{n}{6}}\right)
\end{align*}
\]
因为每个数据值落在控制限之外的概率为 \(p(n)\) ,所以得到一个落在控制限之外的数据值所需的产品数量是一个参数为 \(p(n)\) 的几何随机变量,因此其均值为 \(1 / p(n)\) 。最后,由于每个数据值对应 \(n\) 个产品,所以在 过程 被判定为失控之前生产的物品数量的均值为 \(n / p(n)\) ,所以失控时生产的产品平均数量为:
\[
n/(1 - \Phi(\sqrt{6}-\sqrt{\frac{2n}{3}}))
\]
表 13.2 中给出了不同的 \(n\) 所对应的平均产品数量。由于当 过程 处于受控状态时,\(n\) 的值越大越好(在 过程 被错误地判定为失控之前生产的产品的平均数量约为 \(n / 0.0027\) ),从 表 13.2 中可以明显看出,我们应该至少组合 9 个产品。这意味着每个数据值(等于组合中的缺陷数量)的均值至少为 \(9\times4 = 36\) 。
习题 13.3
1
141
6
74
11
63
16
68
2
162
7
85
12
74
17
95
3
150
8
95
13
103
18
81
4
111
9
76
14
81
19
102
5
92
10
68
15
94
20
73
整个生产过程看起来是否一直处于受控状态?
解 13.3 . \(\overline{X}=94.4\) ,所以控制限为:
\[
\begin{align*}
\text{LCL}&=94.4 - 3\sqrt{94.4}=65.25\\
\text{UCL}&=94.4 + 3\sqrt{94.4}=123.55
\end{align*}
\]
由于前三个数据值大于上控制限(UCL ),删除这三个数据并重新计算样本均值。由此可得:
\(\overline{X}=\frac{(94.4)\times20-(141 + 162+150)}{17}=84.41\)
所以新的控制限为:
\[
\begin{align*}
\text{LCL}&=84.41 - 3\sqrt{84.41}=56.85\\
\text{UCL}&=84.41 + 3\sqrt{84.41}=111.97
\end{align*}
\]
此时,因为其余 17 个数据值都落在控制限内,我们可以宣称该 过程 现在处于受控状态,均值为 84.41。然而,由于在达到受控状态之前,缺陷的平均数量似乎一开始就很高,所以数据值 \(X_4\) 也很可能是在 过程 处于受控状态之前产生的。因此,在这种情况下,需要删除 \(X_4\) 并重新计算似乎是比较谨慎的做法。基于其余 16 个数据值,我们得到:
\[
\begin{align*}
\overline{X}&=82.56\\
\text{LCL}&=82.56 - 3\sqrt{82.56}=55.30\\
\text{UCL}&=82.56 + 3\sqrt{82.56}=109.82
\end{align*}
\]
所以,该过程现在看起来处于受控状态,其均值为 82.56。 \(\blacksquare\)
用于检测总体均值变化的控制图
小节 13.2 \(\overline{X}\) -控制图 的主要缺点在于对总体均值的微小变化不敏感。也就是说,当总体均值出现较小的变化时,由于图中的每个点仅依赖于单个子组,因此往往具有相对较大的方差,所以需要大量的数据点才能检测到总体均值出现的较小的变化。为了解决这个问题,可以让图中的每个数据点不仅取决于最近的子组均值,还取决于其他子组均值。目前,有三种方法可以实现该目的:
移动平均控制图(moving averages )
指数加权移动平均控制图(exponentially weighted moving averages )
累计和控制图(cumulative sum )
移动平均控制图
通过不断绘制最近 \(k\) 个子组的平均值可以得到跨度为 \(k\) 的移动平均控制图。也就是说,在 \(t\) 时刻的移动平均值 \(M_t\) 为:
\(M_t=\frac{\overline{X}_t+\overline{X}_{t - 1}+\cdots+\overline{X}_{t - k + 1}}{k}\)
其中 \(\overline{X}_i\) 是第 \(i\) 个子组的平均值,并且:
\(kM_t=\overline{X}_t+\overline{X}_{t - 1}+\cdots+\overline{X}_{t - k + 1}\)
\(kM_{t + 1}=\overline{X}_{t + 1}+\overline{X}_t+\cdots+\overline{X}_{t - k + 2}\)
于是,\(kM_{t + 1}-kM_t\) 得到:
\(kM_{t + 1}-kM_t=\overline{X}_{t + 1}-\overline{X}_{t - k + 1}\)
即:
\(M_{t + 1}=M_t+\frac{\overline{X}_{t + 1}-\overline{X}_{t - k + 1}}{k}\)
换句话说,\(t + 1\) 时刻的移动平均值等于 \(t\) 时刻的移动平均值加上 \(1/k\) 乘以移动平均值中新添加的值(\(\overline{X}_{t + 1}\) )与需要删除的值(\(\overline{X}_{t - k + 1}\) )之间的差值。当 \(t\) 小于 \(k\) 时,\(M_t\) 定义为前 \(t\) 个子组的平均值,即:
\(M_t=\frac{\overline{X}_1+\cdots+\overline{X}_t}{t} , \quad \text{如果} t < k\)
假设当 过程 处于受控状态时,连续样本数据来自均值为 \(\mu\) 、方差为 \(\sigma^{2}\) 的正态总体。因此,如果子组大小为 \(n\) ,那么 \(\overline{X}_{i}\) 服从均值为 \(\mu\) 、方差为 \(\sigma^{2}/n\) 的正态分布。由此可知,\(m\) 个 \(\overline{X}_{i}\) 的平均值将服从均值为 \(\mu\) 、方差为 \(\text{Var}(\overline{X}_{i})/m=\sigma^{2}/nm\) 的正态分布。所以,当 过程 处于受控状态时:
\[
\begin{align}
E[M_{t}]&=\mu \\
\text{Var}(M_{t}) &=
\begin{cases}
\sigma^{2}/nt & \text{如果 } t < k \\
\sigma^{2}/nk & \text{否则}
\end{cases}
\end{align}
\]
因为正态随机变量几乎总是位于其均值的 3 个标准差内,所以对于 \(M_{t}\) ,我们有以下上、下控制限:
\[
\begin{align}
\text{UCL} &=
\begin{cases}
\mu + 3\sigma/\sqrt{nt} & \text{如果 } t < k \\
\mu + 3\sigma/\sqrt{nk} & \text{否则}
\end{cases} \\
\text{LCL} &=
\begin{cases}
\mu - 3\sigma/\sqrt{nt} & \text{如果 } t < k \\
\mu - 3\sigma/\sqrt{nk} & \text{否则}
\end{cases}
\end{align}
\]
换句话说,除了前 \(k - 1\) 个移动平均值之外,每当移动平均值与 \(\mu\) 的差值超过 \(3\sigma/\sqrt{nk}\) 时,就可以判定 过程 处于失控状态。
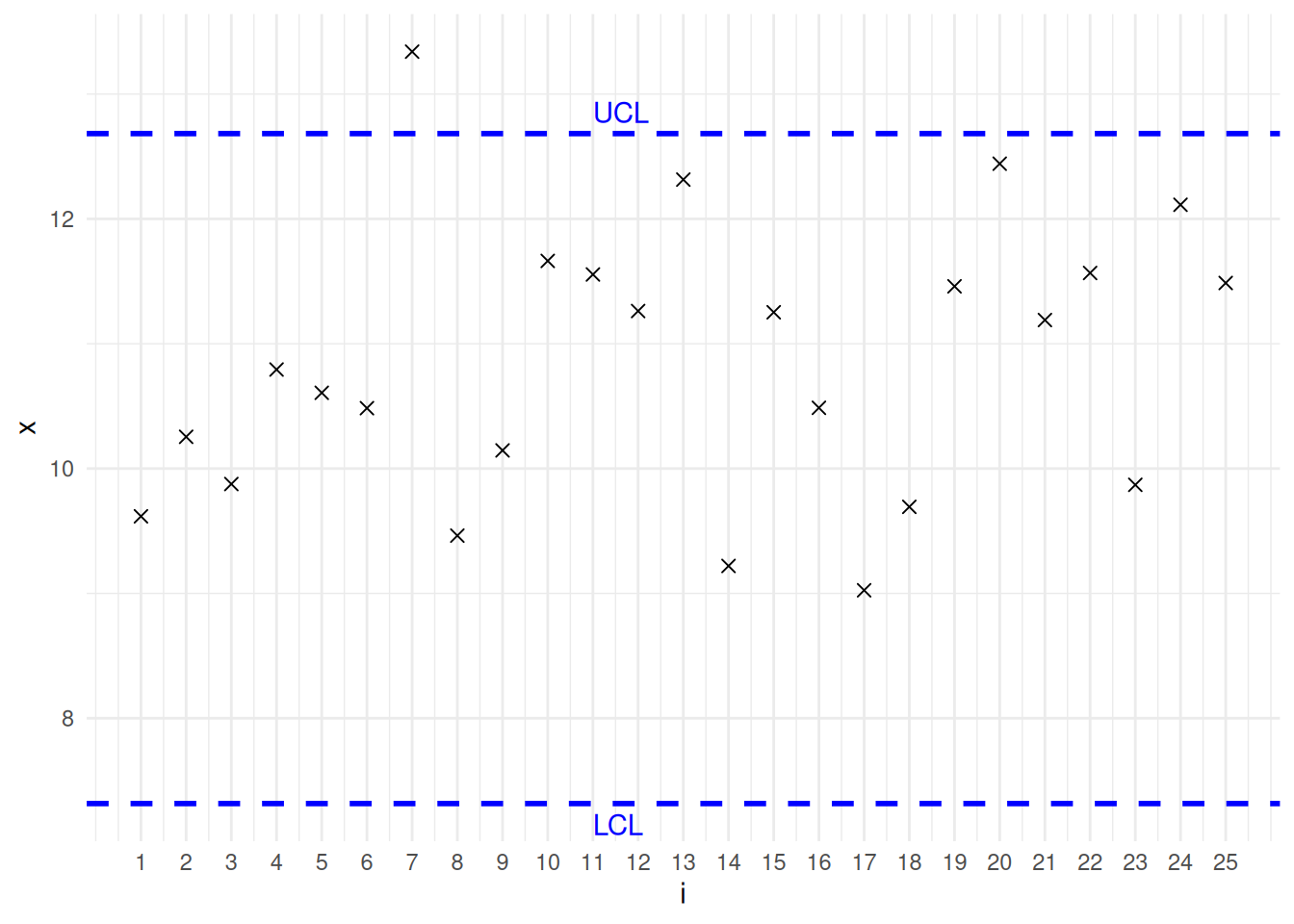
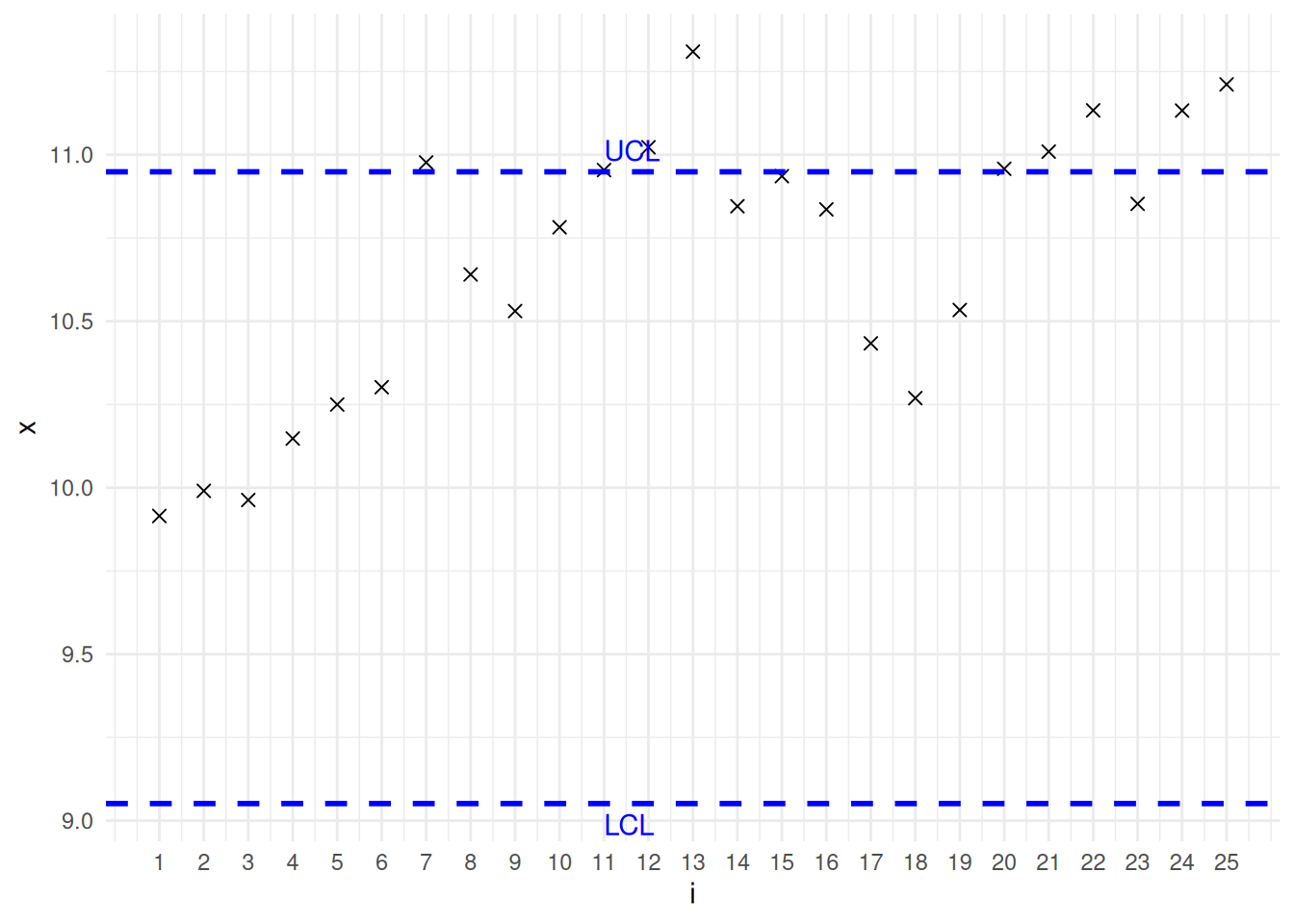
例 13.3 过程 处于受控状态时,其所生产的产品的某测量值服从均值为 10、标准差为 2 的正态分布。以下的模拟数据表示来自均值为 11、标准差为 2 的正态总体的 25 个子组(每个子组大小为 5)的平均值。也就是说,这些数据表示 过程 失控后,其均值从 10 增加到 11 时的子组平均值。表 13.3 给出了这 25 个子组的平均值,以及当 \(k = 8\) 时的移动平均值和上下控制限。对于 \(t>8\) ,下控制限和上控制限分别为 9.051318 和 10.94868。
如表所示,第一个超出其控制限的移动平均值出现在 \(t=11\) ,其他类似情况出现在 12、13、14、16 和 25。有趣的是,通常的控制图——即 \(k = 1\) 的移动平均值——会在 \(t=7\) 时判定 过程 失控,因为 \(\overline{X}_{7}\) 非常大。然而,这是该图唯一会表明 过程 失控的点(见 图 13.3 )。
代码
library (ggplot2)<- c (9.617728 , 10.25437 , 9.876195 , 10.79338 , 10.60699 , 10.48396 , 13.33961 , 9.462969 , 10.14556 , 11.66342 , 11.55484 , 11.26203 , 12.31473 , 9.220009 , 11.25206 , 10.48662 , 9.025091 , 9.693386 , 11.45989 , 12.44213 , 11.18981 , 11.56674 , 9.869849 , 12.11311 , 11.48656 )<- seq_along (x)<- data.frame (i= i, x= x)<- 10 # 均值 <- 2 # 标准差 <- 5 # 子组样本量 <- mu + 3 * sigma / sqrt (n) # 上控制限 <- mu - 3 * sigma / sqrt (n) # 下控制限 ggplot (df, aes (x = i, y = x)) + geom_point (shape = 4 , size = 2 ) + # 绘制均值点 geom_hline (yintercept = UCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 上控制限 geom_hline (yintercept = LCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 下控制限 annotate ("text" , x = 11 , y = UCL, label = "UCL" , hjust = 0 , vjust = - 0.5 , color = "blue" ) + # 标注UCL annotate ("text" , x = 11 , y = LCL, label = "LCL" , hjust = 0 , vjust = 1.5 , color = "blue" ) + # 标注LCL scale_x_continuous (limits = c (1 , 25 ),breaks = seq (1 , 25 , by = 1 )) + theme_minimal () # 使用简洁主题
均值变化大小与合适的移动平均跨度大小 \(k\) 之间往往存在负相关性。也就是说,均值变化越小,\(k\) 的取值应该越大。\(\blacksquare\)
指数加权移动平均控制图
小节 13.6.1 移动平均控制图 在每个 \(t\) 时刻都考虑了到该时刻为止的所有子组平均值的加权平均值,其中最近的 \(k\) 个子组的权重为 \(1/k\) ,其他子组的权重为 0。这似乎是检测总体均值微小变化的最有效的方式,所以也引发了对其他可能性的思考——采用其他的权重来计算加权平均值。
令
\[
W_t=\alpha\overline{X}_t+(1 - \alpha)W_{t - 1}
\tag{13.9}\]
其中 \(\alpha\) 是介于 0 和 1 之间的常数,并且
\(W_0=\mu\)
我们称 \(W_t, t = 0,1,2,\cdots\) 为 指数加权移动平均值 。为了理解为什么要如此称呼这个序列,我们需要注意到:如果不断地用@eq-13_6_1 替换该式右侧的 \(W\) ,我们会得到:
\[
\begin{align*}
W_t&=\alpha\overline{X}_t+(1 - \alpha)[\alpha\overline{X}_{t - 1}+(1 - \alpha)W_{t - 2}] \\
&=\alpha\overline{X}_t+\alpha(1 - \alpha)\overline{X}_{t - 1}+(1 - \alpha)^2W_{t - 2}\\
&=\alpha\overline{X}_t+\alpha(1 - \alpha)\overline{X}_{t - 1}+(1 - \alpha)^2[\alpha\overline{X}_{t - 2}+(1 - \alpha)W_{t - 3}]\\
&=\alpha\overline{X}_t+\alpha(1 - \alpha)\overline{X}_{t - 1}+\alpha(1 - \alpha)^2\overline{X}_{t - 2}+(1 - \alpha)^3W_{t - 3}\\
&\vdots\\
&=\alpha\overline{X}_t+\alpha(1 - \alpha)\overline{X}_{t - 1}+\alpha(1 - \alpha)^2\overline{X}_{t - 2}+\cdots\\
&+\alpha(1 - \alpha)^{t - 1}\overline{X}_1+(1 - \alpha)^t\mu
\end{align*}
\tag{13.10}\]
因此,从 式 13.10 中,我们可以看出,\(W_t\) 是到 \(t\) 时刻为止所有子组平均值的加权平均值,最近的子组的权重为 \(\alpha\) ,然后对于之后的子组不停的乘以 \(1 - \alpha\) 以持续降低其对应子组的权重,最后受控总体均值的权重为 \((1 - \alpha)^t\) 。
\(\alpha\) 的值越小,后续子组的权重就越均匀。例如,如果 \(\alpha = 0.1\) ,那么初始权重是 0.1,后续权重以 0.9 为因子不断减小;也就是说,权重依次是 \(0.1, 0.09, 0.081, 0.073, 0.066, 0.059, \cdots\) 。另一方面,如果 \(\alpha = 0.4\) ,那么权重将依次是 \(0.4, 0.24, 0.144, 0.087, 0.052, \cdots\) 。
由于权重 \(\alpha(1 - \alpha)^{i - 1}, i = 1, 2, \cdots\) ,可以写成
\(\alpha(1 - \alpha)^{i - 1}=\overline{\alpha}e^{-\beta i}\)
其中,\(\overline{\alpha}=\frac{\alpha}{1 - \alpha}, \quad \beta = -\log(1 - \alpha)\)
所以,我们说数据是通过连续的“指数加权” 所得到的。(见 图 13.4 )。
代码
# 设置alpha值 <- 0.4 # 生成i的序列,这里从1到10 <- seq (1 , 10 , 0.1 )# 计算权重 <- alpha * (1 - alpha)^ (i - 1 )# 绘制图形 plot (i, weights, type = "l" , lty = 1 , lwd = 2 , col = "blue" ,xlab = "i" ,ylab = expression (alpha * (1 - alpha)^ (i - 1 )))
为了计算 \(W_t\) 的均值和方差,我们需要回想一下:当 过程 处于受控状态时,子组平均值 \(\overline{X}_i\) 是相互独立的正态随机变量,并且每个子组的平均值的均值为 \(\mu\) 、方差为 \(\sigma^{2}/n\) 。因此,使用 式 13.10 ,有:
\[
\begin{align*}
E[W_t]&=\mu[\alpha+\alpha(1 - \alpha)+\alpha(1 - \alpha)^2+\cdots+\alpha(1 - \alpha)^{t - 1}+(1 - \alpha)^t]\\
&=\frac{\mu\alpha[1-(1 - \alpha)^t]}{1-(1 - \alpha)}+\mu(1 - \alpha)^t\\
&=\mu
\end{align*}
\]
再次使用 式 13.10 以确定方差:
\[
\begin{align*}
\text{Var}(W_t)&=\frac{\sigma^{2}}{n}\left\{\alpha^{2}+[\alpha(1 - \alpha)]^{2}+[\alpha(1 - \alpha)^2]^{2}+\cdots+[\alpha(1 - \alpha)^{t - 1}]^{2}\right\}\\
&=\frac{\sigma^{2}}{n}\alpha^{2}[1+\beta+\beta^{2}+\cdots+\beta^{t - 1}] \quad \text{其中 } \beta=(1 - \alpha)^2\\
&=\frac{\sigma^{2}\alpha^{2}[1-(1 - \alpha)^{2t}]}{n[1-(1 - \alpha)^2]}\\
&=\frac{\sigma^{2}\alpha[1-(1 - \alpha)^{2t}]}{n(2 - \alpha)}
\end{align*}
\]
因此,当 \(t\) 很大时,只要 过程 始终保持在受控状态:
\[
\begin{align*}
E[W_t]&=\mu\\
\text{Var}(W_t)&\approx\frac{\sigma^{2}\alpha}{n(2 - \alpha)} \quad \text{因为 } (1 - \alpha)^{2t}\approx0
\end{align*}
\]
因此,\(W_t\) 的上、下控制限由以下公式给出:
\[
\begin{align*}
\text{UCL}&=\mu + 3\sigma\sqrt{\frac{\alpha}{n(2 - \alpha)}}\\
\text{LCL}&=\mu - 3\sigma\sqrt{\frac{\alpha}{n(2 - \alpha)}}
\end{align*}
\]
注意,当指数加权移动平均控制图的控制限与跨度为 \(k\) 的移动平均控制图(在初始的 \(k\) 个值之后)中的控制限相同时:
\[
\frac{3\sigma}{\sqrt{nk}}=3\sigma\sqrt{\frac{\alpha}{n(2 - \alpha)}}
\]
即,
\[
k=\frac{2 - \alpha}{\alpha} \quad \text{或} \quad \alpha=\frac{2}{k + 1}
\]
习题 13.4 EWMA )控制图,图中每个数据点是连续 4 次维修时间的平均值,且加权因子 \(\alpha = 0.25\) 。如果该控制图的当前值为 60,并且以下是接下来的 16 个子组平均值,我们能得出什么结论?
48, 52, 70, 62, 57, 81, 56, 59, 77, 82, 78, 80, 74, 82, 68, 84
解 13.4 . \(W_0 = 60\) 开始,可以根据公式:
\(W_t = 0.25\overline{X}_t + 0.75W_{t - 1}\)
计算得到 \(W_1,\cdots,W_{16}\) 的连续值。
计算结果如下:
\[
\begin{align*}
W_1&=(0.25)(48)+(0.75)(60)=57\\
W_2&=(0.25)(52)+(0.75)(57)=55.75\\
W_3&=(0.25)(70)+(0.75)(55.75)=59.31\\
W_4&=(0.25)(62)+(0.75)(59.31)=59.98\\
W_5&=(0.25)(57)+(0.75)(59.98)=59.24\\
W_6&=(0.25)(81)+(0.75)(59.24)=64.68
\end{align*}
\]
以此类推,\(W_7\) 到 \(W_{16}\) 的值如下:
\(62.50, 61.61, 65.48, 69.60, 71.70, 73.78, 73.83, 75.87, 73.90, 76.43\)
因为 \(3\sqrt{\frac{0.25}{1.75}}\frac{24}{\sqrt{4}} = 13.61\) ,因此在加权因子 \(\alpha = 0.25\) 时的指数加权移动平均(EWMA )控制图的控制限为:
\[
\begin{align*}
\text{LCL}&=62 - 13.61 = 48.39\\
\text{UCL}&=62 + 13.61 = 75.61
\end{align*}
\]
因此,根据 EWMA 控制图,我们会判断在 \(W_{14}\) (以及 \(W_{16}\) )之后,系统将处于失控状态。另一方面,有趣的是,子组标准差为 \(\sigma/\sqrt{n}=12\) ,但是没有任何一个数据与 \(\mu = 62\) 之间的差距超过了 2 个标准差,所以标准的 \(\overline{X}\) -控制图并不会判定系统失控。\(\blacksquare\)
例 13.4 例 13.3 中的数据,如果使用 \(\alpha=\frac{2}{9}\) 的 EWMA 控制图,我们得到如下的数据(*表示失控)。
1
9.617728
9.915051
14
9.220009
10.84522
2
10.25437
9.990456
15
11.25206
10.93563
3
9.867195
9.963064
16
10.48662
10.83585
4
10.79338
10.14758
17
9.025091
10.43346
5
10.60699
10.24967
18
9.693386
10.269
6
10.48396
10.30174
19
11.45989
10.53364
*7
13.33961
10.97682
*20
12.44213
10.95775
8
9.462969
10.64041
*21
11.18981
11.00932
9
10.14556
10.53044
*22
11.56674
11.13319
10
11.66342
10.78221
23
9.869849
10.85245
*11
11.55484
10.95391
*24
12.11311
11.13259
*12
11.26203
11.02238
*25
11.48656
11.21125
*13
12.31473
11.30957
代码
library (ggplot2)<- c (9.915051 , 9.990456 , 9.963064 , 10.14758 , 10.24967 , 10.30174 , 10.97682 , 10.64041 , 10.53044 , 10.78221 , 10.95391 , 11.02238 , 11.30957 , 10.84522 , 10.93563 , 10.83585 , 10.43346 , 10.269 , 10.53364 , 10.95775 , 11.00932 , 11.13319 , 10.85245 , 11.13259 , 11.21125 )<- seq_along (x)<- data.frame (i= i, x= x)<- 10.94868 # 上控制限 <- 9.051318 # 下控制限 ggplot (df, aes (x = i, y = x)) + geom_point (shape = 4 , size = 2 ) + # 绘制均值点 geom_hline (yintercept = UCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 上控制限 geom_hline (yintercept = LCL, color = "blue" , linetype = "dashed" , size = 1 ) + # 下控制限 annotate ("text" , x = 11 , y = UCL, label = "UCL" , hjust = 0 , vjust = - 0.5 , color = "blue" ) + # 标注UCL annotate ("text" , x = 11 , y = LCL, label = "LCL" , hjust = 0 , vjust = 1.5 , color = "blue" ) + # 标注LCL scale_x_continuous (limits = c (1 , 25 ),breaks = seq (1 , 25 , by = 1 )) + theme_minimal () # 使用简洁主题
因为 \(\text{UCL} = 10.94868, \text{LCL}=9.051318\) ,因此,根据 图 13.5 ,当 \(t=7\) 时,过程 就开始处于失控状态。\(\blacksquare\)
累计和控制图
在检测较小的均值变化或者中等规模的均值变化方面,累计和(通常简称为 cu-sum)控制图也是一种较为有效的检测方法。
假设 \(\overline{X}_1, \overline{X}_2, \cdots\) 表示大小为 \(n\) 的子组的连续平均值,并且当 过程 处于受控状态时,这些随机变量的均值为 \(\mu\) ,标准差为 \(\sigma/\sqrt{n}\) 。最初,假设我们只对检测均值何时增加感兴趣。(单边)累计和控制图可用于检测均值增加的场景,其运作方式如下:
选择大于 0 的常数 \(d\) 和 \(B\) ,并令
\(Y_j = \overline{X}_j - \mu - d\sigma/\sqrt{n}, \quad j\geq1\)
注意,当 过程 处于受控状态时,\(E[\overline{X}_j] = \mu\) ,所以
\(E[Y_j] = -d\sigma/\sqrt{n} < 0\)
现在,令
\(\begin{align*} S_0 &= 0\\ S_{j + 1} &= \max\{S_j + Y_{j + 1}, 0\}, \quad j\geq0 \end{align*}\)
参数为 \(d\) 和 \(B\) 的累计和控制图会持续绘制 \(S_j\) ,并在满足 \(S_j > B\sigma/\sqrt{n}\) 的第一个 \(j\) 时判断均值已经增加。
为了理解这个控制图背后的原理,假设我们决定持续绘制到目前为止观察到的所有随机变量 \(Y_i\) 的总和。也就是说,假设我们决定绘制 \(P_j\) 序列,其中
\(P_j = \sum_{i = 1}^{j}Y_i\) 或者 \(\begin{align*} P_0 &= 0\\ P_{j + 1} &= P_j + Y_{j + 1}, \quad j\geq0 \end{align*}\)
当系统一直处于受控状态时,所有的 \(Y_i\) 的期望值均为负数,因此我们会期望 \(P_j\) 为负数。因此,如果 \(P_j\) 的值变得很大——比如说,大于 \(B\sigma/\sqrt{n}\) ——那么这将是 过程 失控的有力证据。然而,问题在于,如果系统在很长时间后才失控,那么那时 \(P_j\) 的值很可能是非常小的负数(因为在失控之前我们一直在对均值为负数的随机变量求和),因此需要经过很长的时间才能令 \(P_j\) 的值超过 \(B\sigma/\sqrt{n}\) 。因此,为了在 过程 处于受控状态时避免 \(P_j\) 变成非常小的负数,累计和控制图采用了一个简单的技巧:每当 \(P_j\) 变为负数时就将其重置为 0。也就是说,\(S_j\) 是直到时间 \(j\) 为止所有 \(Y_i\) 的累计和(但是,每当所有 \(Y_i\) 的累计总和小于 0 时,\(S_j\) 将被重置为 0)。
例 13.5 \(\mu = 30\) 、\(\sigma/\sqrt{n}=8\) ,考虑绘制参数 \(d = 0.5\) ,\(B = 5\) 的累计和控制图。如果前八个子组的平均值为 29, 33, 35, 42, 36, 44, 43, 45,
那么 \(Y_j=\overline{X}_j - 30 - 4=\overline{X}_j - 34\) 为:
\(Y_1=-5\) ,\(Y_2=-1\) ,\(Y_3 = 1\) ,\(Y_4 = 8\) ,\(Y_5 = 2\) ,\(Y_6 = 10\) ,\(Y_7 = 9\) ,\(Y_8 = 11\)
因此,
\[
\begin{align*}
S_1&=\max\{-5, 0\}=0\\
S_2&=\max\{-1, 0\}=0\\
S_3&=\max\{1, 0\}=1\\
S_4&=\max\{9, 0\}=9\\
S_5&=\max\{11, 0\}=11\\
S_6&=\max\{21, 0\}=21\\
S_7&=\max\{30, 0\}=30\\
S_8&=\max\{41, 0\}=41
\end{align*}
\]
由于控制限为 \(B\sigma/\sqrt{n}=5\times(8)=40\) ,因此根据累计和控制图,在观察到第八个子组的平均值后会,我们将判断均值已经增加。\(\blacksquare\)
为了检测均值的正向或负向变化,我们可以同时使用两个单边累计和控制图。首先,\(E[X_i]\) 的减小等价于 \(E[-X_i]\) 的增加,因此,我们可以通过对子组平均值的负值运行单边累计和控制图来检测产品均值的减小。也就是说,对于指定的参数 \(d\) 和 \(B\) ,我们不仅要像之前那样绘制量 \(S_j\) ,而且还令
\(W_j = -\overline{X}_j - (-\mu) - d\sigma/\sqrt{n}=\mu - \overline{X}_j - d\sigma/\sqrt{n}\)
并且,\(\begin{align*} T_0&=0\\ T_{j + 1}&=\max\{T_j + W_{j + 1}, 0\}, \quad j\geq0 \end{align*}\)
然后也绘制 \(T_j\) 的值。
当 \(S_j\) 或 \(T_j\) 首次超过 \(B\sigma/\sqrt{n}\) 时,就判定 过程 失控。
总之,用于检测所生产产品的均值变化的累计和控制图的步骤如下:
选择大于 0 的常数 \(d\) 和 \(B\)
使用连续的子组平均值来确定 \(S_j\) 和 \(T_j\)
当 \(S_j\) 或 \(T_j\) 首次超过 \(B\sigma/\sqrt{n}\) 时,则判定 过程 失控
\(d\) 和 \(B\) 的取值一般有 3 种:
\(d = 0.25\) ,\(B = 8.00\) \(d = 0.50\) ,\(B = 4.77\) \(d = 1\) ,\(B = 2.49\)
如上的任何一种选择所产生的控制规则的误报率都与在子组平均值与 \(\mu\) 的差值首次超过 \(3\sigma/\sqrt{n}\) 时就判定 过程 失控的 \(\overline{X}\) -控制图大致相同。作为一个通用的经验法则,当想要防范的均值变化越小时,所选的 \(d\) 值就应该越小。